In this note, we give an upper bound for the number of elements from the interval $[1,p^{1/4\sqrt{e}+\unicode[STIX]{x1D716}}]$ necessary to generate the finite field $\mathbb{F}_{p}^{\ast }$ with $p$ an odd prime. The general result depends on the distribution of the divisors of $p-1$ and can be used to deduce results which hold for almost all primes.

We classify all polynomials $P(X)\in \mathbb{Q}[X]$ with rational coefficients having the property that the quotient $(\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{j})/(\unicode[STIX]{x1D706}_{k}-\unicode[STIX]{x1D706}_{\ell })$ is a rational number for all quadruples of roots $(\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D706}_{j},\unicode[STIX]{x1D706}_{k},\unicode[STIX]{x1D706}_{\ell })$ with $\unicode[STIX]{x1D706}_{k}\neq \unicode[STIX]{x1D706}_{\ell }$.

Schmidt [‘Integer points on curves of genus 1’, Compos. Math. 81 (1992), 33–59] conjectured that the number of integer points on the elliptic curve defined by the equation $y^{2}=x^{3}+ax^{2}+bx+c$, with $a,b,c\in \mathbb{Z}$, is $O_{\unicode[STIX]{x1D716}}(\max \{1,|a|,|b|,|c|\}^{\unicode[STIX]{x1D716}})$ for any $\unicode[STIX]{x1D716}>0$. On the other hand, Duke [‘Bounds for arithmetic multiplicities’, Proc. Int. Congress Mathematicians, Vol. II (1998), 163–172] conjectured that the number of algebraic number fields of given degree and discriminant $D$ is $O_{\unicode[STIX]{x1D716}}(|D|^{\unicode[STIX]{x1D716}})$. In this note, we prove that Duke’s conjecture for quartic number fields implies Schmidt’s conjecture. We also give a short unconditional proof of Schmidt’s conjecture for the elliptic curve $y^{2}=x^{3}+ax$.

We describe the ramification in cyclic extensions arising from the Kummer theory of the Weil restriction of the multiplicative group. This generalises the classical theory of Hecke describing the ramification of Kummer extensions.

We investigate images of higher-order differential operators of polynomial algebras over a field 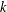$k$. We show that, when 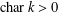$\operatorname{char}k>0$, the image of the set of differential operators 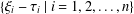$\{\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D70F}_{i}\mid i=1,2,\ldots ,n\}$ of the polynomial algebra 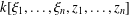$k[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n},z_{1},\ldots ,z_{n}]$ is a Mathieu subspace, where 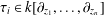$\unicode[STIX]{x1D70F}_{i}\in k[\unicode[STIX]{x2202}_{z_{1}},\ldots ,\unicode[STIX]{x2202}_{z_{n}}]$ for 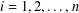$i=1,2,\ldots ,n$. We also show that, when 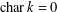$\operatorname{char}k=0$, the same conclusion holds for 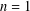$n=1$. The problem concerning images of differential operators arose from the study of the Jacobian conjecture.

We show that every subset of vertices of a directed graph $E$ gives a Morita equivalence between a subalgebra and an ideal of the associated Leavitt path algebra. We use this observation to prove an algebraic version of a theorem of Crisp and Gow: certain subgraphs of $E$ can be contracted to a new graph $G$ such that the Leavitt path algebras of $E$ and $G$ are Morita equivalent. We provide examples to illustrate how desingularising a graph, and in- or out-delaying of a graph, all fit into this setting.

Let ${\mathcal{A}}$ be a unital torsion-free algebra over a unital commutative ring ${\mathcal{R}}$. To characterise Lie $n$-higher derivations on ${\mathcal{A}}$, we give an identity which enables us to transfer problems related to Lie $n$-higher derivations into the same problems concerning Lie $n$-derivations. We prove that: (1) if every Lie $n$-derivation on ${\mathcal{A}}$ is standard, then so is every Lie $n$-higher derivation on ${\mathcal{A}}$; (2) if every linear mapping Lie $n$-derivable at several points is a Lie $n$-derivation, then so is every sequence $\{d_{m}\}$ of linear mappings Lie $n$-higher derivable at these points; (3) if every linear mapping Lie $n$-derivable at several points is a sum of a derivation and a linear mapping vanishing on all $(n-1)$th commutators of these points, then every sequence $\{d_{m}\}$ of linear mappings Lie $n$-higher derivable at these points is a sum of a higher derivation and a sequence of linear mappings vanishing on all $(n-1)$th commutators of these points. We also give several applications of these results.

Let $\unicode[STIX]{x1D70E}=\{\unicode[STIX]{x1D70E}_{i}\mid i\in I\}$ be a partition of the set of all primes $\mathbb{P}$. Let $\unicode[STIX]{x1D70E}_{0}\in \unicode[STIX]{x1D6F1}\subseteq \unicode[STIX]{x1D70E}$ and let $\mathfrak{I}$ be a class of finite $\unicode[STIX]{x1D70E}_{0}$-groups which is closed under extensions, epimorphic images and subgroups. We say that a finite group $G$ is $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-primary provided $G$ is either an $\mathfrak{I}$-group or a $\unicode[STIX]{x1D70E}_{i}$-group for some $\unicode[STIX]{x1D70E}_{i}\in \unicode[STIX]{x1D6F1}\setminus \{\unicode[STIX]{x1D70E}_{0}\}$ and we say that a subgroup $A$ of an arbitrary group $G^{\ast }$ is $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-subnormal in $G^{\ast }$ if there is a subgroup chain $A=A_{0}\leq A_{1}\leq \cdots \leq A_{t}=G^{\ast }$ such that either $A_{i-1}\unlhd A_{i}$ or $A_{i}/(A_{i-1})_{A_{i}}$ is $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-primary for all $i=1,\ldots ,t$. 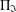We prove that the set ${\mathcal{L}}_{\unicode[STIX]{x1D6F1}_{\mathfrak{I}}}(G)$ of all $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-subnormal subgroups of $G$ forms a sublattice of the lattice of all subgroups of $G$ and we describe the conditions under which the lattice ${\mathcal{L}}_{\unicode[STIX]{x1D6F1}_{\mathfrak{I}}}(G)$ is modular.

We consider stable and almost stable points of autonomous and nonautonomous discrete dynamical systems defined on the closed unit interval. Our considerations are associated with chaos theory by adding an additional assumption that an entropy of a function at a given point is infinite.

The family ${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ of orientation-preserving harmonic functions $f=h+\overline{g}$ in the unit disc $\mathbb{D}$ (normalised in the standard way) satisfying

$$\begin{eqnarray}h^{\prime }(z)+g^{\prime }(z)=\frac{1}{(1+\unicode[STIX]{x1D706}z)(1+\overline{\unicode[STIX]{x1D706}}z)},\quad z\in \mathbb{D},\end{eqnarray}$$

$\unicode[STIX]{x1D706}\in \unicode[STIX]{x2202}\mathbb{D}$

${\mathcal{F}}_{\unicode[STIX]{x1D706}}$

Let $X$ and $Y$ be two normed spaces over fields $\mathbb{F}$ and $\mathbb{K}$, respectively. We prove new generalised hyperstability results for the general linear equation of the form $g(ax+by)=Ag(x)+Bg(y)$, where $g:X\rightarrow Y$ is a mapping and $a,b\in \mathbb{F}$, $A,B\in \mathbb{K}\backslash \{0\}$, using a modification of the method of Brzdęk [‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl.2013 (2013), Art. ID 285, 9 pages]. The hyperstability results of Piszczek [‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc.52 (2015), 1827–1838] can be derived from our main result.

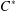We prove a necessary and sufficient condition for embeddability of an operator system into ${\mathcal{O}}_{2}$. Using Kirchberg’s theorems on a tensor product of ${\mathcal{O}}_{2}$ and ${\mathcal{O}}_{\infty }$, we establish results on their operator system counterparts ${\mathcal{S}}_{2}$ and ${\mathcal{S}}_{\infty }$. Applications of the results, including some examples describing $C^{\ast }$-envelopes of operator systems, are also discussed.

We carry out an in-depth study of some domination and smoothing properties of linear operators and of their role within the theory of eventually positive operator semigroups. On the one hand, we prove that, on many important function spaces, they imply compactness properties. On the other hand, we show that these conditions can be omitted in a number of Perron–Frobenius type spectral theorems. We furthermore prove a Kreĭn–Rutman type theorem on the existence of positive eigenvectors and eigenfunctionals under certain eventual positivity conditions.

We consider the split common null point problem in Hilbert space. We introduce and study a shrinking projection method for finding a solution using the resolvent of a maximal monotone operator and prove a strong convergence theorem for the algorithm.

We extend the results of Schu [‘Iterative construction of fixed points of asymptotically nonexpansive mappings’, J. Math. Anal. Appl.158 (1991), 407–413] to monotone asymptotically nonexpansive mappings by means of the Fibonacci–Mann iteration process

$$\begin{eqnarray}x_{n+1}=t_{n}T^{f(n)}(x_{n})+(1-t_{n})x_{n},\quad n\in \mathbb{N},\end{eqnarray}$$

$T$

$\{f(n)\}$

$L_{p}([0,1])$

$1<p<+\infty$

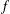We apply a mean-value inequality for positive subsolutions of the $f$-heat operator, obtained from a Sobolev embedding, to prove a nonexistence result concerning complete noncompact $f$-maximal spacelike hypersurfaces in a class of weighted Lorentzian manifolds. Furthermore, we establish a new Calabi–Bernstein result for complete noncompact maximal spacelike hypersurfaces in a Lorentzian product space.

We give a new and simple proof of a result of Ding and Xin, which states that any smooth complete self-shrinker in $\mathbb{R}^{3}$ with the second fundamental form of constant length must be a generalised cylinder $\mathbb{S}^{k}\times \mathbb{R}^{2-k}$ for some $k\leq 2$. Moreover, we prove a gap theorem for smooth self-shrinkers in all dimensions.

The present paper is devoted to complete convergence and the strong law of large numbers under moment conditions near those of the law of the single logarithm (LSL) for independent and identically distributed arrays. More precisely, we investigate limit theorems under moment conditions which are stronger than $2p$ for any $p<2$, in which case we know that there is almost sure convergence to 0, and weaker than $E\,X^{4}/(\log ^{+}|X|)^{2}<\infty$, in which case the LSL holds.