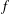Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T13:48:44.288Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXISTENCE OF $f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS

Part of: Global differential geometry Classical differential geometry Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  02 May 2017

ARLANDSON M. S. OLIVEIRA Open the ORCID record for ARLANDSON M. S. OLIVEIRA [Opens in a new window]  and
HENRIQUE F. DE LIMA Open the ORCID record for HENRIQUE F. DE LIMA [Opens in a new window]
ARLANDSON M. S. OLIVEIRA
Affiliation:
Departamento de Matemática, Universidade Federal de Campina Grande, 58429-970 Campina Grande, Paraíba, Brazil email [email protected]
HENRIQUE F. DE LIMA*
Affiliation:
Departamento de Matemática, Universidade Federal de Campina Grande, 58429-970 Campina Grande, Paraíba, Brazil email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We apply a mean-value inequality for positive subsolutions of the 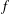$f$-heat operator, obtained from a Sobolev embedding, to prove a nonexistence result concerning complete noncompact $f$-maximal spacelike hypersurfaces in a class of weighted Lorentzian manifolds. Furthermore, we establish a new Calabi–Bernstein result for complete noncompact maximal spacelike hypersurfaces in a Lorentzian product space.

Keywords

weighted Lorentzian product spaceBakry–Émery–Ricci tensorf-Laplacianf-maximal spacelike hypersurfaceentire spacelike graph

MSC classification

Primary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Secondary: 53A07: Higher-dimensional and -codimensional surfaces in Euclidean $n$-space 35P15: Estimation of eigenvalues, upper and lower bounds
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 317 - 325
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author is partially supported by CNPq, Brazil, grant 303977/2015-9.

References

Albujer, A. L., ‘New examples of entire maximal graphs in ℍ2 ×ℝ1 ’, Differ. Geom. Appl. 26 (2008), 456–462.Google Scholar
Aledo, J. A., Romero, A. and Rubio, R. M., ‘Constant mean curvature spacelike hypersurfaces in Lorentzian warped products and Calabi–Bernstein type problems’, Nonlinear Anal. 106 (2014), 57–69.Google Scholar
Alías, L. J. and Colares, A. G., ‘Uniqueness of spacelike hypersurfaces with constant higher order mean curvature in generalized Robertson–Walker spacetimes’, Math. Proc. Cambridge Philos. Soc. 143 (2007), 703–729.Google Scholar
Bakry, D. and Émery, M., ‘Diffusions hypercontractives’, in: Séminaire de Probabilités, XIX, 1983/84, Lecture Notes in Mathematics, 1123 (Springer, Berlin, 1985), 177–206.Google Scholar
Calabi, E., ‘Examples of Bernstein problems for some nonlinear equations’, Proc. Sympos. Pure Math. 15 (1970), 223–230.Google Scholar
Case, J. S., ‘Singularity theorems and the Lorentzian splitting theorem for the Bakry–Émery–Ricci tensor’, J. Geom. Phys. 60 (2010), 477–490.Google Scholar
Charalambous, N. and Lu, Z., ‘The L 1 Liouville property on weighted manifolds’, in: Complex Analysis and Dynamical Systems VI: Part 1: PDE, Differential Geometry, Radon Transform, Contemporary Mathematics, 653 (American Mathematical Society, Providence, RI, 2015), 65–80.Google Scholar
Cheng, S. Y. and Yau, S. T., ‘Maximal space-like hypersurfaces in the Lorentz–Minkowski spaces’, Ann. of Math. 104 (1976), 407–419.Google Scholar
Galloway, G. J., ‘The Lorentzian splitting theorem without the completeness assumption’, J. Differential Geom. 29 (1989), 373–387.Google Scholar
Galloway, G. J. and Woolgar, E., ‘Cosmological singularities in Bakry–Émery spacetimes’, J. Geom. Phys. 86 (2014), 359–369.CrossRefGoogle Scholar
Gromov, M., ‘Isoperimetry of waists and concentration of maps’, Geom. Funct. Anal. 13 (2003), 178–215.CrossRefGoogle Scholar
Hawking, S. W. and Ellis, G. F. R., The Large Scale Structure of Spacetime (Cambridge University Press, London–New York, 1973).CrossRefGoogle Scholar
Impera, D., Pigola, S. and Setti, A. G., ‘Potential theory for manifolds with boundary and applications to controlled mean curvature graphs’, J. reine angew. Math., to appear, doi:10.1515/crelle-2014-0137.Google Scholar
Lichnerowicz, A., ‘Variétés Riemanniennes à tenseur C non négatif’, C. R. Acad. Sci. Paris A–B 271 (1970), A650–A653.Google Scholar
Munteanu, O. and Wang, J., ‘Smooth metric measure spaces with non-negative curvature’, Comm. Anal. Geom. 19 (2011), 451–486.CrossRefGoogle Scholar
O’Neill, B., Semi-Riemannian Geometry with Applications to Relativity (Academic Press, New York, 1983).Google Scholar
Rupert, M. and Woolgar, E., ‘Bakry–Émery black holes’, Classical Quantum Gravity 31 (2014), Article ID 025008, 16 pages.CrossRefGoogle Scholar
Saloff-Coste, L., Aspects of Sobolev-type Inequalities, London Mathematical Society Lecture Note Series, 289 (Cambridge University Press, Cambridge, 2002).Google Scholar
Udrişte, C., Convex Functions and Optimization Methods on Riemannian Manifolds (Springer, Netherlands, 1994).Google Scholar
Woolgar, E., ‘Scalar–tensor gravitation and the Bakry–Émery–Ricci tensor’, Classical Quantum Gravity 30 (2013), Article ID 085007, 8 pages.Google Scholar