Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T07:07:25.608Z Has data issue: false hasContentIssue false
  • English
  • Français

LIE $n$-HIGHER DERIVATIONS AND LIE $n$-HIGHER DERIVABLE MAPPINGS

Part of: Rings and algebras with additional structure Special classes of linear operators

Published online by Cambridge University Press:  09 June 2017

YANA DING Open the ORCID record for YANA DING [Opens in a new window]  and
JIANKUI LI Open the ORCID record for JIANKUI LI [Opens in a new window]
YANA DING
Affiliation:
Department of Mathematics, East China University of Science and Technology, Shanghai, China email [email protected]
JIANKUI LI*
Affiliation:
Department of Mathematics, East China University of Science and Technology, Shanghai, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ${\mathcal{A}}$ be a unital torsion-free algebra over a unital commutative ring 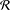${\mathcal{R}}$. To characterise Lie $n$-higher derivations on 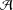${\mathcal{A}}$, we give an identity which enables us to transfer problems related to Lie $n$-higher derivations into the same problems concerning Lie $n$-derivations. We prove that: (1) if every Lie $n$-derivation on 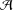${\mathcal{A}}$ is standard, then so is every Lie $n$-higher derivation on 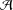${\mathcal{A}}$; (2) if every linear mapping Lie $n$-derivable at several points is a Lie $n$-derivation, then so is every sequence 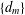$\{d_{m}\}$ of linear mappings Lie $n$-higher derivable at these points; (3) if every linear mapping Lie $n$-derivable at several points is a sum of a derivation and a linear mapping vanishing on all 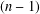$(n-1)$th commutators of these points, then every sequence 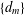$\{d_{m}\}$ of linear mappings Lie $n$-higher derivable at these points is a sum of a higher derivation and a sequence of linear mappings vanishing on all 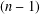$(n-1)$th commutators of these points. We also give several applications of these results.

Keywords

Lie higher derivationLie n-higher derivable mappingLie n-higher derivationLie triple higher derivation

MSC classification

Primary: 16W25: Derivations, actions of Lie algebras
Secondary: 47B47: Commutators, derivations, elementary operators, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 223 - 232
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is partially supported by the National Natural Science Foundation of China, Grant No. 11371136.

References

Abdullaev, I. Z., ‘ n-Lie derivations on von Neumann algebras’, Uzbek. Mat. Zh. 5–6 (1992), 3–9.Google Scholar
Benkovič, D. and Eremita, D., ‘Multiplicative Lie n-derivations of triangular rings’, Linear Algebra Appl. 436 (2012), 4223–4240.Google Scholar
Du, Y. and Wang, Y., ‘Lie derivations of generalized matrix algebras’, Linear Algebra Appl. 437 (2012), 2719–2726.Google Scholar
Fošner, A., Wei, F. and Xiao, Z., ‘Nonlinear Lie-type derivations of von Neumann algebras and related topics’, Colloq. Math. 13 (2013), 53–71.CrossRefGoogle Scholar
Han, D., ‘Lie-type higher derivations on operator algebras’, Bull. Iranian Math. Soc. 40 (2014), 1169–1194.Google Scholar
Hasse, H. and Schmidt, F. K., ‘Noch eine Begründung der Theorie der höheren Differentialquotienten in einem algebraischen Funktionenkörper einer Unbestimmten’, J. reine angew. Math. 177 (1937), 215–223.Google Scholar
Ji, P. and Qi, W., ‘Characterizations of Lie derivations of triangular algebras’, Linear Algebra Appl. 435 (2011), 1137–1146.CrossRefGoogle Scholar
Ji, P., Qi, W. and Sun, X., ‘Characterizations of Lie derivations of factor von Neumann algebras’, Linear Multilinear Algebra 61 (2013), 417–428.Google Scholar
Li, J., Pan, Z. and Shen, Q., ‘Jordan and Jordan higher all-derivable points of some algebras’, Linear Multilinear Algebra 61 (2013), 831–845.Google Scholar
Liu, L., ‘Lie triple derivations on factor von Neumann algebras’, Bull. Korean Math. Soc. 52 (2015), 581–591.Google Scholar
Longstaff, W. E. and Panaia, O., ‘J-subspace lattices and subspace M-bases’, Studia Math. 139 (2000), 197–212.Google Scholar
Lu, F. and Jing, W., ‘Characterizations of Lie derivations of B (X)’, Linear Algebra Appl. 432 (2010), 89–99.Google Scholar
Mirzavaziri, M., ‘Characterization of higher derivations on algebras’, Comm. Algebra 38 (2010), 981–987.Google Scholar
Qi, X., ‘Characterization of (generalized) Lie derivations on J-subspace lattice algebras by local action’, Aequationes Math. 87 (2014), 53–69.Google Scholar
Qi, X., ‘Characterizing Lie n-derivations for reflexive algebras’, Linear Multilinear Algebra 63 (2015), 1693–1706.Google Scholar
Qi, X. and Hou, J., ‘Characterization of Lie derivations on prime rings’, Comm. Algebra 39 (2011), 3824–3835.CrossRefGoogle Scholar
Qi, X. and Hou, J., ‘Characterization of Lie derivations on von Neumann algebras’, Linear Algebra Appl. 438 (2013), 533–548.CrossRefGoogle Scholar
Wang, Y., ‘Lie n-derivations of unital algebras with idempotents’, Linear Algebra Appl. 458 (2014), 512–525.Google Scholar