Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T06:19:48.772Z Has data issue: false hasContentIssue false
  • English
  • Français

IMAGES OF HIGHER-ORDER DIFFERENTIAL OPERATORS OF POLYNOMIAL ALGEBRAS

Part of: Differential algebra Affine geometry

Published online by Cambridge University Press:  09 June 2017

DAYAN LIU  and
XIAOSONG SUN Open the ORCID record for XIAOSONG SUN [Opens in a new window]
DAYAN LIU
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, China email [email protected]
XIAOSONG SUN*
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate images of higher-order differential operators of polynomial algebras over a field 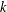$k$. We show that, when 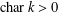$\operatorname{char}k>0$, the image of the set of differential operators 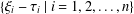$\{\unicode[STIX]{x1D709}_{i}-\unicode[STIX]{x1D70F}_{i}\mid i=1,2,\ldots ,n\}$ of the polynomial algebra 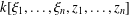$k[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n},z_{1},\ldots ,z_{n}]$ is a Mathieu subspace, where 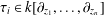$\unicode[STIX]{x1D70F}_{i}\in k[\unicode[STIX]{x2202}_{z_{1}},\ldots ,\unicode[STIX]{x2202}_{z_{n}}]$ for 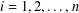$i=1,2,\ldots ,n$. We also show that, when 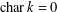$\operatorname{char}k=0$, the same conclusion holds for 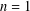$n=1$. The problem concerning images of differential operators arose from the study of the Jacobian conjecture.

Keywords

image conjecturedifferential operatorsMathieu subspacesJacobian conjecture

MSC classification

Primary: 13N10: Rings of differential operators and their modules
Secondary: 14R15: Jacobian problem
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 205 - 211
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the NSF of China (11401249, 11371165) and the STDPF of Jilin Province, China (20150520051JH, 20150101001JC).

References

Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
Bass, H., Connel, E. and Wright, D., ‘The Jacobian conjecture: reduction of degree and formal expansion of the inverse’, Bull. Amer. Math. Soc. 7 (1982), 287–330.Google Scholar
van den Essen, A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathematics, 190 (Birkhäuser, Basel, 2000).Google Scholar
van den Essen, A., ‘The amazing image conjecture’, Preprint, 2010, arXiv:1006.5801.Google Scholar
van den Essen, A., Wright, D. and Zhao, W., ‘Images of locally finite derivations of polynomial algebras in two variables’, J. Pure Appl. Algebra 215(9) (2011), 2130–2134.Google Scholar
van den Essen, A., Wright, D. and Zhao, W., ‘On the image conjecture’, J. Algebra 340(1) (2011), 211–224.Google Scholar
van den Essen, A. and Zhao, W., ‘Mathieu subspaces of univariate polynomial algebras’, J. Pure Appl. Algebra 217(9) (2013), 1316–1324.Google Scholar
Mathieu, O., ‘Some conjectures about invariant theory and their applications’, in: Algèbre non Commutative, groupes quantiques et invariants, Reims, 1995, Sémin. Congr., 2 (Soc. Math. France, Paris, 1997), 263–279.Google Scholar
Zhao, W., ‘Images of commuting differential operators of order one with constant leading coefficients’, J. Algebra 324(2) (2010), 231–247.Google Scholar
Zhao, W., ‘Generalizations of the image conjecture and the Mathieu conjecture’, J. Pure Appl. Algebra 214(7) (2010), 1200–1216.Google Scholar
Zhao, W., ‘Mathieu subspaces of associative algebras’, J. Algebra 350(1) (2012), 245–272.Google Scholar