Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T13:21:15.740Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLETE CONVERGENCE FOR ARRAYS AND THE LAW OF THE SINGLE LOGARITHM

Part of: Distribution theory - Probability Stochastic processes Limit theorems

Published online by Cambridge University Press:  29 August 2017

ALLAN GUT  and
ULRICH STADTMÜLLER Open the ORCID record for ULRICH STADTMÜLLER [Opens in a new window]
ALLAN GUT
Affiliation:
Department of Mathematics, Uppsala University, Box 480, SE-751 06 Uppsala, Sweden email [email protected]
ULRICH STADTMÜLLER*
Affiliation:
Department of Number Theory and Probability Theory, Ulm University, D-89069 Ulm, Germany email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The present paper is devoted to complete convergence and the strong law of large numbers under moment conditions near those of the law of the single logarithm (LSL) for independent and identically distributed arrays. More precisely, we investigate limit theorems under moment conditions which are stronger than 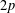$2p$ for any 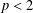$p<2$, in which case we know that there is almost sure convergence to 0, and weaker than 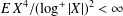$E\,X^{4}/(\log ^{+}|X|)^{2}<\infty$, in which case the LSL holds.

Keywords

arraysrow-wise independenceindependent and identically distributedthe law of the iterated logarithmcomplete convergencethe strong law of large numbersBorel–Cantelli lemmasexponential bounds

MSC classification

Primary: 60F15: Strong theorems
Secondary: 60E15: Inequalities; stochastic orderings 60G50: Sums of independent random variables; random walks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 333 - 344
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Bingham, N. H., ‘Variants on the law of the iterated logarithm’, Bull. Lond. Math. Soc. 18 (1986), 433–467.Google Scholar
Chow, Y. S., ‘Delayed sums and Borel summability for independent, identically distributed random variables’, Bull. Inst. Math. Acad. Sin. 1 (1973), 207–220.Google Scholar
Erdős, P., ‘On a theorem of Hsu and Robbins’, Ann. Math. Statist. 20 (1949), 286–291.Google Scholar
Erdős, P., ‘Remark on my paper ‘On a theorem of Hsu and Robbins’’, Ann. Math. Statist. 21 (1950), 138.Google Scholar
Gut, A., ‘Complete convergence for arrays’, Period. Math. Hungar. 25 (1992), 51–75.Google Scholar
Gut, A., ‘The weak law of large numbers for arrays’, Statist. Probab. Lett. 14 (1992), 49–52.Google Scholar
Gut, A., Probability: A Graduate Course, 2nd edn (Springer, New York, 2013).Google Scholar
Gut, A. and Stadtmüller, U., ‘Strong laws for sequences in the vicinity of the LIL’, Statist. Probably. Lett. 122 (2017), 63–72.CrossRefGoogle Scholar
Gut, A. and Stadtmüller, U., ‘Almost sure limit behavior of Cesàro sums with small order’, Acta Math. Hung. 151 (2017), 510–530.Google Scholar
Hartman, P. and Wintner, A., ‘On the law of the iterated logarithm’, Amer. J. Math. 63 (1941), 169–176.CrossRefGoogle Scholar
Hoffmann-Jørgensen, L., Miao, Y., Li, X. C. and Xu, S. F., ‘Kolmogorov type law of the logarithm for arrays’, J. Theoret. Probab. 29 (2016), 32–47.Google Scholar
Hsu, P. L. and Robbins, H., ‘Complete convergence and the law of large numbers’, Proc. Natl. Acad. Sci. USA 33 (1947), 25–31.CrossRefGoogle ScholarPubMed
Marcinkiewicz, J. and Zygmund, A., ‘Sur les fonctions indépendantes’, Fund. Math. 29 (1937), 60–90.Google Scholar
Qi, Y.-C., ‘On strong convergence of arrays’, Bull. Aust. Math. Soc. 50 (1994), 219–223.Google Scholar
Stadtmüller, U., ‘A note on the law of iterated logarithm for weighted sums of random variables’, Ann. Probab. 12 (1984), 35–44.Google Scholar
Strassen, V., ‘A converse to the law of the iterated logarithm’, Z. Wahrscheinlichkeitsth. verw. Geb. 4 (1966), 265–268.Google Scholar
Sung, S. H., ‘An analogue of Kolmogorov’s law of the iterated logarithm for arrays’, Bull. Aust. Math. Soc. 54 (1996), 177–182.Google Scholar