Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T16:15:33.531Z Has data issue: false hasContentIssue false
  • English
  • Français

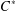EMBEDDINGS AND $C^{\ast }$-ENVELOPES OF EXACT OPERATOR SYSTEMS

Part of: Linear spaces and algebras of operators Selfadjoint operator algebras

Published online by Cambridge University Press:  02 May 2017

PREETI LUTHRA  and
AJAY KUMAR Open the ORCID record for AJAY KUMAR [Opens in a new window]
PREETI LUTHRA
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India email [email protected]
AJAY KUMAR*
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a necessary and sufficient condition for embeddability of an operator system into 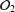${\mathcal{O}}_{2}$. Using Kirchberg’s theorems on a tensor product of 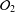${\mathcal{O}}_{2}$ and 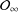${\mathcal{O}}_{\infty }$, we establish results on their operator system counterparts 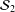${\mathcal{S}}_{2}$ and 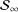${\mathcal{S}}_{\infty }$. Applications of the results, including some examples describing 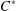$C^{\ast }$-envelopes of operator systems, are also discussed.

Keywords

operator systemsexactnessC∗ -envelopesCuntz algebrastensor products

MSC classification

Primary: 46L06: Tensor products of $C^*$-algebras
Secondary: 46L05: General theory of $C^*$-algebras 46L07: Operator spaces and completely bounded maps 47L25: Operator spaces (= matricially normed spaces)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 274 - 285
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Argerami, M. and Farenick, D., ‘The C*-envelope of an irreducible periodic weighted unilateral shift’, Integral Equations Operator Theory 77(2) (2013), 199–210.Google Scholar
Argerami, M. and Farenick, D., ‘C*-envelopes of Jordan operator systems’, Oper. Matrices 9(2) (2015), 325–341.Google Scholar
Arveson, W. B., ‘Subalgebras of C ∗ -algebras’, Acta Math. 123(1) (1969), 141–224.Google Scholar
Bratteli, O., Elliott, G. A., Evans, D. E. and Kishimoto, A., ‘On the classification of C ∗ -algebras of real rank zero III. The infinite case’, in: Operator Algebras and their Applications, II (Waterloo, Ontario, 1994/1995), Fields Institute Comm., 20 (1998), 11–72.Google Scholar
Cuntz, J., ‘Simple C*-algebra generated by isometries’, Comm. Math. Phys. 57(2) (1977), 173–185.Google Scholar
Farenick, D., Kavruk, A. S., Paulsen, V. I. and Todorov, I. G., ‘Operator systems from discrete groups’, Comm. Math. Phys. 329(1) (2014), 207–238.Google Scholar
Gupta, V. P. and Luthra, P., ‘Operator system nuclearity via C ∗ -envelopes’, J. Aust. Math. Soc. 101(3) (2016), 356–375.Google Scholar
Hamana, M., ‘Injective envelopes of operator systems’, Publ. Res. Inst. Math. Sci. 15(3) (1979), 773–785.Google Scholar
Kavruk, A. S., ‘Nuclearity related properties in operator systems’, J. Operator Theory 71(1) (2014), 95–156.Google Scholar
Kavruk, A. S., Paulsen, V. I., Todorov, I. G. and Tomforde, M., ‘Tensor products of operator systems’, J. Funct. Anal. 261(2) (2011), 267–299.Google Scholar
Kavruk, A. S., Paulsen, V. I., Todorov, I. G. and Tomforde, M., ‘Quotients, exactness, and nuclearity in the operator system category’, Adv. Math. 235 (2013), 321–360.Google Scholar
Kirchberg, E. and Phillips, C. N., ‘Embedding of exact C ∗ -algebras into 𝓞2 ’, J. reine angew. Math. 525 (2000), 17–53.CrossRefGoogle Scholar
Kirchberg, E. and Wassermann, S., ‘C*-algebras generated by operator systems’, J. Funct. Anal. 155(2) (1998), 324–351.Google Scholar
Lupini, M., ‘Fraïssé limits in functional analysis’, Preprint, 2015, arXiv:1510.05188.Google Scholar
Lupini, M., ‘Operator space and operator system analogs of Kirchberg’s nuclear embedding theorem’, J. Math. Anal. Appl. 431(1) (2015), 47–56.Google Scholar
Ortiz, C. M. and Paulsen, V. I., ‘Lovász theta type norms and operator systems’, Linear Algebra Appl. 477 (2015), 128–147.Google Scholar
Paulsen, V. I. and Zheng, D., ‘Tensor products of the operator system generated by the Cuntz isometries’, J. Operator Theory 76(1) (2016), 67–91.Google Scholar
Pisier, G., Introduction to Operator Space Theory, London Mathematical Society Lecture Note Series, 294 (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Rørdam, M., Classification of Nuclear, Simple C ∗ -Algebras (Springer, Berlin, 2002).Google Scholar
Takesaki, M., Theory of Operator Algebras II, Vol. 125 (Springer Science & Business Media, Berlin, 2013).Google Scholar
Zheng, D., ‘The operator system generated by Cuntz isometries’, Preprint, 2014, arXiv:1410.6950.Google Scholar