Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T16:33:10.039Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS

Part of: Geometric function theory Two-dimensional theory

Published online by Cambridge University Press:  07 August 2017

ÁLVARO FERRADA-SALAS ,
RODRIGO HERNÁNDEZ  and
MARÍA J. MARTÍN
ÁLVARO FERRADA-SALAS
Affiliation:
Facultad de Matemáticas, Pontificia Universidad Católica de Chile, Casilla 306, Santiago, Chile email [email protected]
RODRIGO HERNÁNDEZ
Affiliation:
Facultad de Ingeniería y Ciencias, Universidad Adolfo Ibáñez, Av. Padre Hurtado 750, Viña del Mar, Chile email [email protected]
MARÍA J. MARTÍN*
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, PO Box 111, FI-80101 Joensuu, Finland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The family 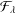${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ of orientation-preserving harmonic functions 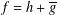$f=h+\overline{g}$ in the unit disc 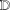$\mathbb{D}$ (normalised in the standard way) satisfying

$$\begin{eqnarray}h^{\prime }(z)+g^{\prime }(z)=\frac{1}{(1+\unicode[STIX]{x1D706}z)(1+\overline{\unicode[STIX]{x1D706}}z)},\quad z\in \mathbb{D},\end{eqnarray}$$
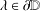for some $\unicode[STIX]{x1D706}\in \unicode[STIX]{x2202}\mathbb{D}$, along with their rotations, play an important role among those functions that are harmonic and orientation-preserving and map the unit disc onto a convex domain. The main theorem in this paper generalises results in recent literature by showing that convex combinations of functions in 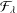${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ are convex.

Keywords

convex harmonic mappingsconvex combinations

MSC classification

Primary: 31A05: Harmonic, subharmonic, superharmonic functions
Secondary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 256 - 262
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The second and third authors are supported by Fondecyt, Chile, grant 1150284. The third author is also partially supported by grant MTM2015-65792-P from MINECO/FEDER, the Thematic Research Network MTM2015-69323-REDT, MINECO, Spain, and the Academy of Finland, grant 268009.

References

Boyd, Z., Dorff, M., Nowak, M., Romney, M. and Wołoszkiewicz, M., ‘Univalency of convolutions of harmonic mappings’, Appl. Math. Comput. 234 (2014), 326–332.Google Scholar
Clunie, J. and Sheil-Small, T., ‘Harmonic univalent functions’, Ann. Acad. Sci. Fenn. Ser. A. I Math. 9 (1984), 3–25.Google Scholar
Dorff, M. J., ‘Harmonic univalent mappings onto asymmetric vertical strips’, in: Computational Methods and Function Theory 1997 (eds. Papamichael, N., Ruscheweyh, S. and Saff, E. B.) (World Science Publishing, River Edge, NJ, 1999), 171–175.Google Scholar
Duren, P., Harmonic Mappings in the Plane (Cambridge University Press, Cambridge, 2004).Google Scholar
Ferrada-Salas, A., ‘Affine and linearly invariant families, generalized harmonic Koebe functions, and analytic and geometric properties of convex harmonic mappings (Spanish)’, PhD Thesis, Pontificia Universidad Católica de Chile, Santiago, Chile, 2015.Google Scholar
Hengartner, W. and Schober, G., ‘Univalent harmonic functions’, Trans. Amer. Math. Soc. 299 (1987), 1–31.Google Scholar
Hernández, R. and Martín, M. J., ‘Stable geometric properties of analytic and harmonic functions’, Math. Proc. Cambridge Philos. Soc. 155 (2013), 343–359.CrossRefGoogle Scholar
Lewy, H., ‘On the non-vanishing of the Jacobian in certain one-to-one mappings’, Bull. Amer. Math. Soc. 42 (1936), 689–692.Google Scholar
Li, L.-L. and Ponnusamy, S., ‘Convolutions of slanted half-plane harmonic mappings’, Analysis (Munich) 33 (2013), 159–176.Google Scholar
Royster, W. C. and Ziegler, M., ‘Univalent functions convex in one direction’, Publ. Math. Debrecen 23 (1976), 339–345.Google Scholar
Sun, Y., Jiang, Y.-P. and Wang, Z.-G., ‘On the convex combinations of slanted half-plane harmonic mappings’, J. Math. Anal. 6 (2015), 46–50.Google Scholar
Sun, Y., Rasila, A. and Jiang, T.-P., ‘Linear combinations of harmonic quasiconformal mappings convex in one direction’, Kodai Math. J. 39 (2016), 366–377.CrossRefGoogle Scholar
Wang, Z.-G., Liu, Z.-H. and Li, Y.-C., ‘On the linear combinations of harmonic univalent mappings’, J. Math. Anal. Appl. 400 (2013), 452–459.Google Scholar