Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T17:08:42.763Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE GENERALISED HYPERSTABILITY OF THE GENERAL LINEAR EQUATION

Part of: Nonlinear operators and their properties

Published online by Cambridge University Press:  29 August 2017

LADDAWAN AIEMSOMBOON  and
WUTIPHOL SINTUNAVARAT
LADDAWAN AIEMSOMBOON
Affiliation:
Department of Mathematics and Statistics, Faculty of Science and Technology, Thammasat University Rangsit Center, Pathumthani 12121, Thailand email [email protected]
WUTIPHOL SINTUNAVARAT*
Affiliation:
Department of Mathematics and Statistics, Faculty of Science and Technology, Thammasat University Rangsit Center, Pathumthani 12121, Thailand email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

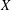Let $X$ and 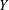$Y$ be two normed spaces over fields 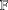$\mathbb{F}$ and 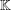$\mathbb{K}$, respectively. We prove new generalised hyperstability results for the general linear equation of the form 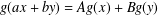$g(ax+by)=Ag(x)+Bg(y)$, where 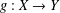$g:X\rightarrow Y$ is a mapping and 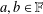$a,b\in \mathbb{F}$, 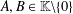$A,B\in \mathbb{K}\backslash \{0\}$, using a modification of the method of Brzdęk [‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl.2013 (2013), Art. ID 285, 9 pages]. The hyperstability results of Piszczek [‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc.52 (2015), 1827–1838] can be derived from our main result.

Keywords

fixed pointgeneralised hyperstabilitygeneral linear equation

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Secondary: 39B62: Functional inequalities, including subadditivity, convexity, etc. 47H10: Fixed-point theorems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 263 - 273
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by a Research Professional Development Project under the Science Achievement Scholarship of Thailand (SAST); the second author was also supported by the Thailand Research Fund and Office of the Higher Education Commission under grant no. MRG5980242.

References

Aiemsomboon, L. and Sintunavarat, W., ‘Two new generalised hyperstability results for the Drygas functional equation’, Bull. Aust. Math. Soc. 95(2) (2017), 269–280.Google Scholar
Aoki, T., ‘On the stability of the linear transformation in Banach spaces’, J. Math. Soc. Japan 2 (1950), 64–66.Google Scholar
Bourgin, D. G., ‘Approximately isometric and multiplicative transformations on continuous function rings’, Duke Math. J. 16 (1949), 385–397.Google Scholar
Brzdęk, J., ‘Hyperstability of the Cauchy equation on restricted domains’, Acta Math. Hungar. 141 (2013), 58–67.Google Scholar
Brzdęk, J., ‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl. 2013 (2013), Art. ID 285, 9 pages.CrossRefGoogle Scholar
Brzdęk, J., ‘Remarks on stability of some inhomogeneous functional equations’, Aequationes Math. 89 (2015), 83–96.CrossRefGoogle Scholar
Brzdęk, J., Chudziak, J. and Páles, Zs., ‘A fixed point approach to stability of functional equations’, Nonlinear Anal. 74 (2011), 6728–6732.Google Scholar
Brzdęk, J. and Pietrzyk, A., ‘A note on stability of the general linear equation’, Aequationes Math. 75 (2008), 267–270.Google Scholar
Gajda, Z., ‘On stability of additive mappings’, Int. J. Math. Math. Sci. 14 (1991), 431–434.CrossRefGoogle Scholar
Gǎvruţa, P., ‘A generalization of the Hyers–Ulam–Rassias stability of approximately additive mapping’, J. Math. Anal. Appl. 184 (1994), 431–436.Google Scholar
Hyers, D. H., ‘On the stability of the linear functional equation’, Proc. Natl. Acad. Sci. USA 27 (1941), 222–224.Google Scholar
Hyers, D. H., Isac, G. and Rassias, Th. M., Stability of Functional Equations in Several Variables (Birkhäuser, Berlin, 1998).Google Scholar
Kuczma, M., An Introduction to the Theory of Functional Equations and Inequalities (PWN, Warszawa, 1985).Google Scholar
Maksa, Gy. and Páles, Zs., ‘Hyperstability of a class of linear functional equations’, Acta Math. Acad. Paedagog. Nyházi. (N.S.) 17 (2001), 107–112.Google Scholar
Piszczek, M., ‘Remark on hyperstability of the general linear equation’, Aequationes Math. 88 (2014), 163–168.CrossRefGoogle Scholar
Piszczek, M., ‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc. 52 (2015), 1827–1838.CrossRefGoogle Scholar
Popa, D., ‘Hyers–Ulam–Rassias stability of the general linear equation’, Nonlinear Funct. Anal. Appl. 7 (2002), 581–588.Google Scholar
Rassias, Th. M., ‘On the stability of the linear mapping in Banach spaces’, Proc. Amer. Math. Soc. 72 (1978), 297–300.CrossRefGoogle Scholar
Rassias, Th. M., ‘On a modified Hyers–Ulam sequence’, J. Math. Anal. Appl. 158 (1991), 106–113.Google Scholar