Let 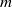 $m$,
$m$,  $a$,
$a$,  $c$ be positive integers with
$c$ be positive integers with 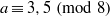 $a\equiv 3, 5~({\rm mod} \hspace{0.334em} 8)$. We show that when
$a\equiv 3, 5~({\rm mod} \hspace{0.334em} 8)$. We show that when 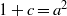 $1+ c= {a}^{2} $, the exponential Diophantine equation
$1+ c= {a}^{2} $, the exponential Diophantine equation 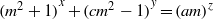 $\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $ has only the positive integer solution
$\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $ has only the positive integer solution 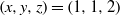 $(x, y, z)= (1, 1, 2)$ under the condition
$(x, y, z)= (1, 1, 2)$ under the condition 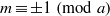 $m\equiv \pm 1~({\rm mod} \hspace{0.334em} a)$, except for the case
$m\equiv \pm 1~({\rm mod} \hspace{0.334em} a)$, except for the case 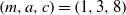 $(m, a, c)= (1, 3, 8)$, where there are only two solutions:
$(m, a, c)= (1, 3, 8)$, where there are only two solutions: 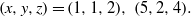 $(x, y, z)= (1, 1, 2), ~(5, 2, 4). $ In particular, when
$(x, y, z)= (1, 1, 2), ~(5, 2, 4). $ In particular, when 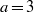 $a= 3$, the equation
$a= 3$, the equation 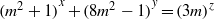 $\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(8{m}^{2} - 1)}\nolimits ^{y} = \mathop{(3m)}\nolimits ^{z} $ has only the positive integer solution
$\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(8{m}^{2} - 1)}\nolimits ^{y} = \mathop{(3m)}\nolimits ^{z} $ has only the positive integer solution 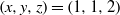 $(x, y, z)= (1, 1, 2)$, except if
$(x, y, z)= (1, 1, 2)$, except if 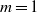 $m= 1$. The proof is based on elementary methods and Baker’s method.
$m= 1$. The proof is based on elementary methods and Baker’s method.
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$
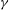 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma $-VECTORS AND THE DERIVATIVES OF THE TANGENT AND SECANT FUNCTIONS
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\gamma $-VECTORS AND THE DERIVATIVES OF THE TANGENT AND SECANT FUNCTIONS
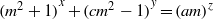 $\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $
$\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $
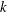 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
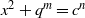 ${x}^{2} + {q}^{m} = {c}^{n} $
${x}^{2} + {q}^{m} = {c}^{n} $