Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T10:54:13.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Double Character Sums over Subgroups and Intervals

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  15 May 2014

MEI-CHU CHANG  and
IGOR E. SHPARLINSKI
MEI-CHU CHANG
Affiliation:
Department of Mathematics, University of California, Riverside, CA 92521, USA email [email protected]
IGOR E. SHPARLINSKI*
Affiliation:
Department of Pure Mathematics, University of New South Wales, Sydney, NSW 2052, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We estimate double sums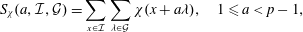

$$\begin{eqnarray}S_{{\it\chi}}(a,{\mathcal{I}},{\mathcal{G}})=\mathop{\sum }\limits_{x\in {\mathcal{I}}}\mathop{\sum }\limits_{{\it\lambda}\in {\mathcal{G}}}{\it\chi}(x+a{\it\lambda}),\quad 1\leq a<p-1,\end{eqnarray}$$
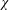with a multiplicative character ${\it\chi}$ modulo 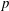$p$ where 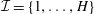${\mathcal{I}}=\{1,\dots ,H\}$ and 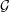${\mathcal{G}}$ is a subgroup of order 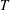$T$ of the multiplicative group of the finite field of 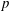$p$ elements. A nontrivial upper bound on 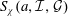$S_{{\it\chi}}(a,{\mathcal{I}},{\mathcal{G}})$ can be derived from the Burgess bound if 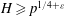$H\geq p^{1/4+{\it\varepsilon}}$ and from some standard elementary arguments if 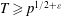$T\geq p^{1/2+{\it\varepsilon}}$, where 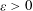${\it\varepsilon}>0$ is arbitrary. We obtain a nontrivial estimate in a wider range of parameters 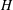$H$ and 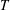$T$. We also estimate double sums
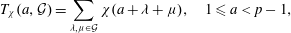$$\begin{eqnarray}T_{{\it\chi}}(a,{\mathcal{G}})=\mathop{\sum }\limits_{{\it\lambda},{\it\mu}\in {\mathcal{G}}}{\it\chi}(a+{\it\lambda}+{\it\mu}),\quad 1\leq a<p-1,\end{eqnarray}$$
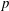 and give an application to primitive roots modulo $p$ with three nonzero binary digits.

Keywords

character sumsintervalsmultiplicative subgroups of finite fields

MSC classification

Primary: 11L40: Estimates on character sums
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 376 - 390
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Ayyad, A., Cochrane, T. and Zheng, Z., ‘The congruence x 1x 2≡ x 3x 4(mod p), the equationx 1x 2= x 3x 4and the mean value of character sums’, J. Number Theory 59 (1996), 398–413.CrossRefGoogle Scholar
Bourgain, J., ‘Mordell’s exponential sum estimate revisited’, J. Amer. Math. Soc. 18 (2005), 477–499.Google Scholar
Bourgain, J., ‘On the distribution of the residues of small multiplicative subgroups of Fp’, Israel J. Math. 172 (2009), 61–74.Google Scholar
Bourgain, J., ‘On exponential sums in finite fields’, in: An Irregular Mind, János Bolyai Math. Soc., 21 (Budapest, 2010), 219–242.Google Scholar
Bourgain, J., ‘Sum-product theorems and applications’, in: Additive Number Theory (Springer, Berlin, 2010), 9–38.CrossRefGoogle Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, I. E., ‘On the hidden shifted power problem’, SIAM J. Comput. 41 (2012), 1524–1557.CrossRefGoogle Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, I. E., ‘On congruences with products of variables from short intervals and applications’, Proc. Steklov Math. Inst. 280 (2013), 67–96.CrossRefGoogle Scholar
Bourgain, J., Glibichuk, A. A. and Konyagin, S. V., ‘Estimates for the number of sums and products and for exponential sums in fields of prime order’, J. Lond. Math. Soc. 73 (2006), 380–398.CrossRefGoogle Scholar
Bourgain, J., Konyagin, S. V. and Shparlinski, I. E., ‘Product sets of rationals, multiplicative translates of subgroups in residue rings and fixed points of the discrete logarithm’, Intern. Math. Res. Notices 2008 (2008), 1–29; Corrigenda: Intern. Math. Res. Notices 2009 (2009), 3146–3147.Google Scholar
Bourgain, J., Konyagin, S. V. and Shparlinski, I. E., ‘Distribution of elements of cosets of small subgroups and applications’, Intern. Math. Res. Notices 2012 (2012), 1968–2009.Google Scholar
Bourgain, J., Konyagin, S. V. and Shparlinski, I. E., ‘Character sums and deterministic polynomial root finding in finite fields’, Math. Comp., to appear.Google Scholar
Chang, M.-C., ‘On a question of Davenport and Lewis and new character sum bounds in finite fields’, Duke Math. J. 145 (2008), 409–442.CrossRefGoogle Scholar
Davenport, H. and Erdős, P., ‘The distribution of quadratic and higher residues’, Publ. Math. Debrecen 2 (1952), 252–265.CrossRefGoogle Scholar
Drmota, M. and Tichy, R., Sequences, Discrepancies and Applications (Springer, Berlin, 1997).CrossRefGoogle Scholar
Friedlander, J. B. and Iwaniec, H., ‘Estimates for character sums’, Proc. Amer. Math. Soc. 119 (1993), 365–372.CrossRefGoogle Scholar
Dietmann, R., Elsholtz, C. and Shparlinski, I. E., ‘On gaps between quadratic non-residues in the Euclidean and Hamming metrics’, Indag. Math. 24 (2013), 930–938.Google Scholar
Garaev, M. Z., ‘Sums and products of sets and estimates of rational trigonometric sums in fields of prime order’, Russian Math. Surveys 65 (2010), 599–658; translation from Uspekhi Mat. Nauk.CrossRefGoogle Scholar
Gómez-Pérez, D. and Shparlinski, I. E., ‘Subgroups generated by polynomials in finite fields’, Preprint, arXiv:1309.7378.Google Scholar
Heath-Brown, D. R. and Konyagin, S. V., ‘New bounds for Gauss sums derived from kth powers, and for Heilbronn’s exponential sum’, Quart. J. Math. 51 (2000), 221–235.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
Karatsuba, A. A., ‘The distribution of values of Dirichlet characters on additive sequences’, Dokl. Acad. Sci. USSR 319 (1991), 543–545 (in Russian).Google Scholar
Karatsuba, A. A., ‘Weighted character sums’, Izv. Ross. Akad. Nauk Ser. Mat. (Transl. as Izv. Math.) 64(2) (2000), 29–42 (in Russian).Google Scholar
Karatsuba, A. A., ‘Arithmetic problems in the theory of Dirichlet characters’, Uspekhi Mat. Nauk. (Transl. as Russian Math. Surveys) 63(4) (2008), 43–92 (in Russian).Google Scholar
Kerr, B., ‘Incomplete exponential sums over exponential functions’, Preprint, arXiv:1302.4170.Google Scholar
S. V., Konyagin, ‘Bounds of exponential sums over subgroups and Gauss sums’, Proc. 4th Int. Conf. on Modern Problems of Number Theory and its Applications, Moscow Lomonosov State University, Moscow, 2002, 86–114 (in Russian).Google Scholar
Konyagin, S. V. and Shparlinski, I. E., ‘On the consecutive powers of a primitive root: Gaps and exponential sums’, Mathematika 58 (2012), 11–20.Google Scholar
Shao, X., ‘Character sums over unions of intervals’, Forum Math., to appear.Google Scholar
Shkredov, I. D., ‘Some new inequalities in additive combinatorics’, Moscow J. Combin. Number Theory, to appear.Google Scholar
Shkredov, I. D., ‘On exponential sums over multiplicative subgroups of medium size’, Preprint, arXiv:1311.5726.Google Scholar
Shparlinski, I. E., ‘Polynomial values in small subgroups of finite fields’, Preprint,arXiv:1401.0964.Google Scholar