Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Deng, Mou-Jie
2015.
A note on the Diophantine equation $x^{2} + q^{m} = c^{2n}$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 91,
Issue. 2,
DENG, MOU-JIE
GUO, JIN
and
XU, AI-JUAN
2018.
A NOTE ON THE DIOPHANTINE EQUATION .
Bulletin of the Australian Mathematical Society,
Vol. 98,
Issue. 2,
p.
188.
Fujita, Y.
and
Terai, N.
2020.
On The Generalized Ramanujan–Nagell Equation $$x^2+(2c-1)^m=c^n$$.
Acta Mathematica Hungarica,
Vol. 162,
Issue. 2,
p.
518.
Yu, Yahui
and
Hu, Jiayuan
2021.
On the generalized Ramanujan-Nagell equation $ x^2+(2k-1)^y = k^z $ with $ k\equiv 3 $ (mod 4).
AIMS Mathematics,
Vol. 6,
Issue. 10,
p.
10596.
Alahmadi, Adel
and
Luca, Florian
2022.
On a result of Fujita and Le.
Acta Scientiarum Mathematicarum,
Vol. 88,
Issue. 3-4,
p.
577.
Mutlu, Elif Kızıldere
Le, Maohua
and
Soydan, Gökhan
2022.
A modular approach to the generalized Ramanujan–Nagell equation.
Indagationes Mathematicae,
Vol. 33,
Issue. 5,
p.
992.
von Känel, Rafael
and
Matschke, Benjamin
2023.
Solving 𝑆-unit, Mordell, Thue, Thue–Mahler and Generalized Ramanujan–Nagell Equations via the Shimura–Taniyama Conjecture.
Memoirs of the American Mathematical Society,
Vol. 286,
Issue. 1419,
Fujita, Yasutsugu
Le, Maohua
and
Terai, Nobuhiro
2023.
On two generalized Ramanujan–Nagell equations.
Indian Journal of Pure and Applied Mathematics,
Mutlu, Elif Kızıldere
Le, Maohua
and
Soydan, Gökhan
2024.
An elementary approach to the generalized Ramanujan–Nagell equation.
Indian Journal of Pure and Applied Mathematics,
Vol. 55,
Issue. 1,
p.
392.
Nam, Pham Hong
2025.
On the Diophantine equation $~(p^n)^x+(4^mp+1)^y=z^2~$ when $~p, 4^mp+1~$ are prime numbers.
International Electronic Journal of Algebra,
Vol. 37,
Issue. 37,
p.
190.
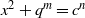 ${x}^{2} + {q}^{m} = {c}^{n} $
${x}^{2} + {q}^{m} = {c}^{n} $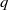 $q$ be an odd prime such that
$q$ be an odd prime such that 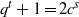 ${q}^{t} + 1= 2{c}^{s} $, where
${q}^{t} + 1= 2{c}^{s} $, where 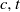 $c, t$ are positive integers and
$c, t$ are positive integers and 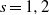 $s= 1, 2$. We show that the Diophantine equation
$s= 1, 2$. We show that the Diophantine equation 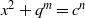 ${x}^{2} + {q}^{m} = {c}^{n} $ has only the positive integer solution
${x}^{2} + {q}^{m} = {c}^{n} $ has only the positive integer solution 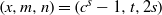 $(x, m, n)= ({c}^{s} - 1, t, 2s)$ under some conditions. The proof is based on elementary methods and a result concerning the Diophantine equation
$(x, m, n)= ({c}^{s} - 1, t, 2s)$ under some conditions. The proof is based on elementary methods and a result concerning the Diophantine equation 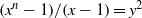 $({x}^{n} - 1)/ (x- 1)= {y}^{2} $ due to Ljunggren. We also verify that when
$({x}^{n} - 1)/ (x- 1)= {y}^{2} $ due to Ljunggren. We also verify that when 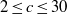 $2\leq c\leq 30$ with
$2\leq c\leq 30$ with 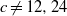 $c\not = 12, 24$, the Diophantine equation
$c\not = 12, 24$, the Diophantine equation 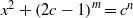 ${x}^{2} + \mathop{(2c- 1)}\nolimits ^{m} = {c}^{n} $ has only the positive integer solution
${x}^{2} + \mathop{(2c- 1)}\nolimits ^{m} = {c}^{n} $ has only the positive integer solution 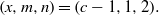 $(x, m, n)= (c- 1, 1, 2). $
$(x, m, n)= (c- 1, 1, 2). $