Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T02:19:18.437Z Has data issue: false hasContentIssue false
  • English
  • Français

ON DEFICIENT-PERFECT NUMBERS

Part of: Elementary number theory

Published online by Cambridge University Press:  23 May 2014

MIN TANG  and
MIN FENG
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China email [email protected]
MIN FENG
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a positive integer $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n$, let 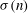$\sigma (n)$ denote the sum of the positive divisors of $n$. Let 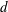$d$ be a proper divisor of $n$. We call $n$ a deficient-perfect number if 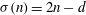$\sigma (n) = 2n - d$. In this paper, we show that there are no odd deficient-perfect numbers with three distinct prime divisors.

Keywords

almost perfect numberdeficient-perfect numbernear-perfect number

MSC classification

Secondary: 11A25: Arithmetic functions; related numbers; inversion formulas
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 186 - 194
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Anavi, A., Pollack, P. and Pomerance, C., ‘On congruences of the form σ (n) = a (mod n)’, Int. J. Number Theory 9 (2013), 115–124.CrossRefGoogle Scholar
Cohen, G. L., ‘On odd perfect numbers (II), multiperfect numbers and quasiperfect numbers’, J. Aust. Math. Soc. 29 (1980), 369–384.Google Scholar
Hagis, P. and Cohen, G. L., ‘Some results concerning quasiperfect numbers’, J. Aust. Math. Soc. 33 (1982), 275–286.Google Scholar
Kishore, M., ‘Odd integers n with five distinct prime factors for which 2 − 10−12 < σ (n)∕n < 2 + 10−12’, Math. Comp. 32 (1978), 303–309.Google Scholar
Pollack, P. and Shevelev, V., ‘On perfect and near-perfect numbers’, J. Number Theory 132 (2012), 3037–3046.Google Scholar
Ren, X. Z. and Chen, Y. G., ‘On near-perfect numbers with two distinct prime factors’, Bull. Aust. Math. Soc. 88 (2013), 520–524.Google Scholar
Sándor, J., Mitrinović, D. S. and Crstici, B., Handbook of Number Theory I (Springer, Dordrecht, The Netherlands, 2005).Google Scholar
Tang, M., Ren, X. Z. and Li, M., ‘On near-perfect and deficient-perfect numbers’, Colloq. Math. 133 (2013), 221–226.Google Scholar