Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T02:33:44.733Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A CLASS OF SUPERSOLUBLE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  23 May 2014

A. BALLESTER-BOLINCHES ,
J. C. BEIDLEMAN ,
R. ESTEBAN-ROMERO  and
M. F. RAGLAND
A. BALLESTER-BOLINCHES*
Affiliation:
Departament d’Àlgebra, Universitat de València, Dr. Moliner, 50, 46100 Burjassot, València, Spain email [email protected]
J. C. BEIDLEMAN
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY 40506-0027, USA email [email protected]
R. ESTEBAN-ROMERO
Affiliation:
Institut Universitari de Matemàtica Pura i Aplicada, Universitat Politècnica de València, Camí de Vera, s/n, 46022 València, Spain email [email protected]
M. F. RAGLAND
Affiliation:
Department of Mathematics, Auburn University at Montgomery, PO Box 244023, Montgomery, AL 36124-4023, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subgroup 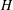$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ of a finite group 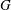$G$ is said to be S-semipermutable in 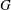$G$ if 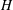$H$ permutes with every Sylow 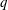$q$-subgroup of 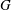$G$ for all primes 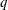$q$ not dividing 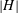$|H |$. A finite group 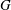$G$ is an MS-group if the maximal subgroups of all the Sylow subgroups of 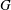$G$ are S-semipermutable in 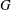$G$. The aim of the present paper is to characterise the finite MS-groups.

Keywords

finite groupsoluble PST-groupT0-groupMS-groupBT-group

MSC classification

Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20D15: Nilpotent groups, $p$-groups 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 220 - 226
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Al-Sharo, K. A., Beidleman, J. C., Heineken, H. and Ragland, M. F., ‘Some characterizations of finite groups in which semipermutability is a transitive relation’, Forum Math. 22(5) (2010), 855–862; Corrigendum: Forum Math. 24(6) (2012), 1333–1334.CrossRefGoogle Scholar
Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of Finite Groups, de Gruyter Expositions in Mathematics, 53 (Walter de Gruyter, Berlin, 2010).CrossRefGoogle Scholar
Ballester-Bolinches, A., Esteban-Romero, R. and Pedraza-Aguilera, M. C., ‘On a class of p-soluble groups’, Algebra Colloq. 12(2) (2005), 263–267.CrossRefGoogle Scholar
Beidleman, J. C. and Ragland, M. F., ‘Groups with maximal subgroups of Sylow subgroups satisfying certain permutability conditions’, Southeast Asian Bull. Math., to appear.Google Scholar
Kegel, O. H., ‘Sylow-Gruppen und Subnormalteiler endlicher Gruppen’, Math. Z. 78 (1962), 205–221.Google Scholar
Ragland, M. F., ‘Generalizations of groups in which normality is transitive’, Comm. Algebra 35(10) (2007), 3242–3252.CrossRefGoogle Scholar
Ren, Y. C., ‘Notes on π-quasi-normal subgroups in finite groups’, Proc. Amer. Math. Soc. 117 (1993), 631–636.Google Scholar
van der Waall, R. W. and Fransman, A., ‘On products of groups for which normality is a transitive relation on their Frattini factor groups’, Quaest. Math. 19 (1996), 59–82.Google Scholar
Wang, L., Li, Y. and Wang, Y., ‘Finite groups in which (S-)semipermutability is a transitive relation’, Int. J. Algebra 2(3) (2008), 143–152; Corrigendum: Int. J. Algebra 6(15) (2012), 727–728.Google Scholar