Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-10T08:10:21.760Z Has data issue: false hasContentIssue false
  • English
  • Français

A GROUP SUM INEQUALITY AND ITS APPLICATION TO POWER GRAPHS

Part of: Special aspects of infinite or finite groups Graph theory

Published online by Cambridge University Press:  13 June 2014

BRIAN CURTIN  and
G. R. POURGHOLI
BRIAN CURTIN*
Affiliation:
Department of Mathematics and Statistics, University of South Florida, Tampa, FL 33620, USA email [email protected]
G. R. POURGHOLI
Affiliation:
School of Mathematics, Statistics and Computer Science, University of Tehran, Tehran 14155-6455, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 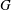$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a finite group of order $n$, and let 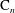$\text {C}_n$ be the cyclic group of order $n$. For 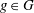$g\in G$, let 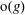${\mathrm{o}}(g)$ denote the order of 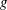$g$. Let 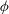$\phi $ denote the Euler totient function. 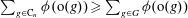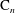We show that $\sum _{g \in \text {C}_n} \phi ({\mathrm{o}}(g))\geq \sum _{g \in G} \phi ({\mathrm{o}}(g))$, with equality if and only if $G$ is isomorphic to $\text {C}_n$. As an application, we show that among all finite groups of a given order, the cyclic group of that order has the maximum number of bidirectional edges in its directed power graph.

Keywords

cyclic groupsEuler totientSylow subgroups

MSC classification

Secondary: 20F99: None of the above, but in this section 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 418 - 426
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Abawajy, J., Kelarev, A. and Chowdhury, M., ‘Power graphs: a survey’, Electron. J. Graph Theory Appl. 1(2) (2013), 125–147.Google Scholar
Amiri, H., Jafarian Amiri, S. M. and Isaacs, I. M., ‘Sums of element orders in finite groups’, Comm. Algebra 37(9) (2009), 2978–2980.CrossRefGoogle Scholar
Burton, D. M., Elementary Number Theory, 5th edn (McGraw-Hill, Boston, MA, 2002).Google Scholar
Curtin, B. and Pourgholi, G. R., ‘Edge-maximality of power graphs of finite cyclic groups’, J. Algebraic Combin., to appear. Online first edition doi: 10.1007/s10801-013-0490-5; arXiv:1311.2984.Google Scholar
Kelarev, A. V. and Quinn, S. J., ‘A combinatorial property and power graphs of groups’, in: Contributions to General Algebra, 12 (Vienna, 1999) (Heyn, Klagenfurt, 2000), 229–235.Google Scholar
Kelarev, A. V. and Quinn, S. J., ‘Directed graph and combinatorial properties of semigroups’, J. Algebra 251(1) (2002), 16–26.Google Scholar
Kelarev, A. V. and Quinn, S. J., ‘A combinatorial property and power graphs of semigroups’, Comment. Math. Univ. Carolin. 45 (2004), 1–7.Google Scholar
Kelarev, A. V., Quinn, S. J. and Smolikova, R., ‘Power graphs and semigroups of matrices’, Bull. Aust. Math. Soc. 63(2) (2001), 341–344.Google Scholar
Rose, J. S., A Course on Group Theory (Dover Publications, New York, 1994).Google Scholar