No CrossRef data available.
Article contents
(STRONGLY) GORENSTEIN FLAT MODULES OVER GROUP RINGS
Part of:
Rings and algebras arising under various constructions
Connections with homological algebra and category theory
Modules, bimodules and ideals
Published online by Cambridge University Press: 17 December 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let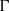 
$\Gamma $ be a group and 
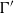${\Gamma }^{\prime } $ be a subgroup of 
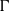$\Gamma $ of finite index. Let 
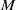$M$ be a 
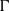$\Gamma $-module. It is shown that 
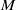$M$ is (strongly) Gorenstein flat if and only if it is (strongly) Gorenstein flat as a 
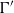${\Gamma }^{\prime } $-module. We also provide some criteria in which the classes of Gorenstein projective and strongly Gorenstein flat 
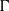$\Gamma $-modules are the same.
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Asadollahi, J., Bahlekeh, A., Hajizamani, A. and Salarian, Sh., ‘On certain homological invariants of groups’, J. Algebra 333 (2011), 18–35.CrossRefGoogle Scholar
Asadollahi, J., Bahlekeh, A. and Salarian, Sh., ‘On the hierarchy of cohomological dimensions of groups’, J. Pure Appl. Algebra 213 (2009), 1795–1803.Google Scholar
Auslander, M. and Bridger, M., ‘Stable module theory’, Mem. Amer. Math. Soc. 94 (1969).Google Scholar
Avramov, M. and Martsinkovsky, A., ‘Absolute, relative and Tate cohomology of modules of finite Gorenstein dimension’, Proc. Lond. Math. Soc. (3) 85 (2) (2002), 392–440.CrossRefGoogle Scholar
Bahlekeh, A., Dembegioti, F. and Talelli, O., ‘Gorenstein dimension and proper actions’, Bull. Lond. Math. Soc. 41 (2009), 859–871.Google Scholar
Bahlekeh, A. and Salarian, Sh., ‘New results related to a conjecture of Moore’, Arch. Math. 100 (2013), 231–239.Google Scholar
Bennis, D., ‘A note on Gorenstein flat dimension’, Algebra Colloquium 18 (2011), 155–161.Google Scholar
Bennis, D. and Mahdou, N., ‘Strongly Gorenstein projective, injective and flat modules’, J. Pure Appl. Algebra 210 (2) (2007), 437–445.Google Scholar
Benson, D. J., ‘Flat modules over group rings of finite groups’, Algebr. Represent. Theory 2 (1999), 287–294.CrossRefGoogle Scholar
Cornick, J. and Kropholler, P. H., ‘Homological finiteness conditions for modules over group algebras’, J. Lond. Math. Soc. 2 (58) (1997), 49–62.Google Scholar
Ding, N., Li, Y. and Mao, L., ‘Strongly Gorenstein flat modules’, J. Aust. Math. Soc. 86 (3) (2009), 323–338.CrossRefGoogle Scholar
Enochs, E. and Jenda, O. M. G., ‘Gorenstein injective and projective modules’, Math. Z. 220 (1995), 611–633.CrossRefGoogle Scholar
Enochs, E. E., Jenda, O. M. G. and Torrecillas, B., ‘Gorenstein flat modules’, Nanjing Daxue Xuebao Shuxue Bannian Kan 10 (1993), 1–9.Google Scholar
Gillespie, J., ‘Model structures on modules over Ding-Chen rings’, Homology Homotopy Appl. 12 (1) (2010), 61–73.CrossRefGoogle Scholar
Holm, H., ‘Gorenstein homological dimensions’, J. Pure Appl. Algebra 189 (1–3) (2004), 167–193.CrossRefGoogle Scholar
Ikenaga, B. M., ‘Homological dimension and Farrell cohomology’, J. Algebra 87 (1984), 422–457.CrossRefGoogle Scholar
Jensen, C. U., ‘On the vanishing of 
$\lim _{\overleftarrow {i} }$’, J. Algebra 15 (1970), 151–166.CrossRefGoogle Scholar
$\lim _{\overleftarrow {i} }$’, J. Algebra 15 (1970), 151–166.CrossRefGoogle ScholarKropholler, P. H., ‘On groups of type $F{P}_{\infty } $’, J. Pure Appl. Algebra 90 (1993), 55–67.CrossRefGoogle Scholar
$F{P}_{\infty } $’, J. Pure Appl. Algebra 90 (1993), 55–67.CrossRefGoogle ScholarMahdou, N. and Tamekkante, M., ‘Strongly Gorenstein flat modules and dimensions’, Chin. Ann. Math. 32 B (2011), 533–548.Google Scholar
Zhang, C. X. and Wang, L. M., ‘Strongly Gorenstein flat dimensions’, J. Math. Res. Exposition 31 (6) (2011), 977–988.Google Scholar
You have
Access