Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T12:21:35.874Z Has data issue: false hasContentIssue false
  • English
  • Français

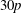PENTAVALENT SYMMETRIC GRAPHS OF ORDER $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$

Part of: Graph theory

Published online by Cambridge University Press:  27 August 2014

BO LING ,
CI XUAN WU  and
BEN GONG LOU
BO LING
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunmin 650031, PR China email [email protected]
CI XUAN WU
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunmin 650031, PR China email [email protected]
BEN GONG LOU*
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunmin 650031, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

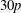A complete classification is given of pentavalent symmetric graphs of order $30p$, where 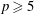$p\ge 5$ is a prime. It is proved that such a graph 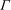${\Gamma }$ exists if and only if 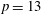$p=13$ and, up to isomorphism, there is only one such graph. Furthermore, 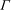${\Gamma }$ is isomorphic to 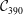$\mathcal{C}_{390}$, a coset graph of PSL(2, 25) with 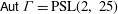${\sf Aut}\, {\Gamma }=\mbox{PSL(2, 25)}$, and 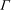${\Gamma }$ is 2-regular. The classification involves a new 2-regular pentavalent graph construction with square-free order.

Keywords

arc-transitive graphpentavalent symmetric graphautomorphism group

MSC classification

Secondary: 05C30: Enumeration in graph theory 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 353 - 362
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Alaeiyan, M., Talebi, A. A. and Paryab, K., ‘Arc-transitive Cayley graphs of valency five on abelian groups’, SEAMS Bull. Math. 32 (2008), 1029–1035.Google Scholar
Bosma, W., Cannon, C. and Playoust, C., ‘The MAGMA algebra system I: The user language’, J. Symbolic Comput. 24 (1997), 235–265.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups (Clarendon Press, Oxford, 1985).Google Scholar
Du, S. F., Marušič, D. and Waller, A. O., ‘On 2-arc-transitive covers of complete graphs’, J. Combin. Theory Ser. B 74 (1998), 276–290.CrossRefGoogle Scholar
Giudici, M., Li, C. H. and Praeger, C. E., ‘Analysing finite locally s-arc transitive graphs’, Trans. Amer. Math. Soc. 356 (2004), 291–317.Google Scholar
Gorenstein, D., Finite Simple Groups (Plenum Press, New York, 1982).Google Scholar
Guo, D. C., ‘A classification of symmetric graphs of order 30’, Australas. J. Combin. 15 (1997), 277–294.Google Scholar
Guo, S. T. and Feng, Y. Q., ‘A note on pentavalent s-transitive graphs’, Discrete Math. 312 (2012), 2214–2216.Google Scholar
Guo, S. T., Feng, Y. Q. and Li, C. H., ‘The finite edge-primitive pentavalent graphs’, J. Algebraic Combin. 38 (2013), 491–497.Google Scholar
Guo, S. T., Zhou, J. X. and Feng, Y. Q., ‘Pentavalent symmetric graphs of order 12p’, Electron. J. Combin. 18 (2011), 233.Google Scholar
Hua, X. H. and Feng, Y. Q., ‘Pentavalent symmetric graphs of order 8p’, J. Beijing Jiaotong Univ. 35 (2011), 132–135; 141.Google Scholar
Hua, X. H. and Feng, Y. Q., ‘Pentavalent symmetric graphs of order 2p q’, Discrete Math. 311 (2011), 2259–2267.CrossRefGoogle Scholar
Karpilovsky, G., The Schur Multiplier, London Mathematical Society Monographs, New Series, 2 (Clarendon Press, Oxford, 1987).Google Scholar
Li, C. H. and Pan, J. M., ‘Finite 2-arc-transitive abelian Cayley graphs’, European J. Combin. 29 (2008), 148–158.Google Scholar
Li, Y. T. and Feng, Y. Q., ‘Pentavalent one-regular graphs of square-free order’, Algebra. Colloq. 17 (2010), 515–524.Google Scholar
Lorimer, P., ‘Vertex-transitive graphs: Symmetric graphs of prime valency’, J. Graph Theory 8 (1984), 55–68.Google Scholar
Pan, J. M., Lou, B. G. and Liu, C. F., ‘Arc-transitive pentavalent graphs of order 4p q’, Electron. J. Combin. 20(1) (2013), 36.Google Scholar
Pan, J. M., Yu, X. and Yu, X. F., ‘Pentavalent symmetric graphs of order twice a prime square’, Algebra. Colloq., to appear.Google Scholar
Praeger, C. E., ‘An O’Nan-Scott theorem for finite quasiprimitive permutation groups and an application to 2-arc-transitive graphs’, J. London. Math. Soc. 47 (1992), 227–239.Google Scholar
Sabidussi, G. O., ‘Vertex-transitive graphs’, Monatsh. Math. 68 (1984), 426–438.Google Scholar
Zhou, J. X. and Feng, Y. Q., ‘On symmetric graphs of valency five’, Discrete Math. 310 (2010), 1725–1732.Google Scholar