We give complexity analysis for the class of short generating functions. Assuming #P$\not \subseteq$FP/poly, we show that this class is not closed under taking many intersections, unions or projections of generating functions, in the sense that these operations can increase the bit length of coefficients of generating functions by a super-polynomial factor. We also prove that truncated theta functions are hard for this class.

The Hajnal–Szemerédi theorem states that for any positive integer $r$ and any multiple $n$ of $r$, if $G$ is a graph on $n$ vertices and $\unicode[STIX]{x1D6FF}(G)\geqslant (1-1/r)n$, then $G$ can be partitioned into $n/r$ vertex-disjoint copies of the complete graph on $r$ vertices. We prove a very general analogue of this result for directed graphs: for any positive integer $r$ with $r\neq 3$ and any sufficiently large multiple $n$ of $r$, if $G$ is a directed graph on $n$ vertices and every vertex is incident to at least $2(1-1/r)n-1$ directed edges, then $G$ can be partitioned into $n/r$ vertex-disjoint subgraphs of size $r$ each of which contain every tournament on $r$ vertices (the case $r=3$ is different and was handled previously). In fact, this result is a consequence of a tiling result for standard multigraphs (that is multigraphs where there are at most two edges between any pair of vertices). A related Turán-type result is also proven.

We determine systematic vanishing regions for the bigraded homotopy sheaves of the motivic sphere spectrum over a field of characteristic different from two.

In this paper we use tools from differential topology to give a geometric description of cohomology for Hilbert manifolds. Our model is Quillen’s geometric description of cobordism groups for finite-dimensional smooth manifolds [Quillen, ‘Elementary proofs of some results of cobordism theory using steenrod operations’, Adv. Math., 7 (1971)]. Quillen stresses the fact that this construction allows the definition of Gysin maps for ‘oriented’ proper maps. For finite-dimensional manifolds one has a Gysin map in singular cohomology which is based on Poincaré duality, hence it is not clear how to extend it to infinite-dimensional manifolds. But perhaps one can overcome this difficulty by giving a Quillen type description of singular cohomology for Hilbert manifolds. This is what we do in this paper. Besides constructing a general Gysin map, one of our motivations was a geometric construction of equivariant cohomology, which even for a point is the cohomology of the infinite-dimensional space $BG$, which has a Hilbert manifold model. Besides that, we demonstrate the use of such a geometric description of cohomology by several other applications. We give a quick description of characteristic classes of a finite-dimensional vector bundle and apply it to a generalized Steenrod representation problem for Hilbert manifolds and define a notion of a degree of proper oriented Fredholm maps of index $0$.

We consider the Cauchy problem for the cubic fourth order nonlinear Schrödinger equation (4NLS) on the circle. In particular, we prove global well-posedness of the renormalized 4NLS in negative Sobolev spaces 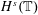$H^{s}(\mathbb{T})$, 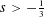$s>-\frac{1}{3}$, with enhanced uniqueness. The proof consists of two separate arguments. (i) We first prove global existence in 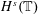$H^{s}(\mathbb{T})$, 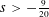$s>-\frac{9}{20}$, via the short-time Fourier restriction norm method. By following the argument in Guo–Oh for the cubic NLS, this also leads to nonexistence of solutions for the (nonrenormalized) 4NLS in negative Sobolev spaces. (ii) We then prove enhanced uniqueness in 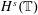$H^{s}(\mathbb{T})$, 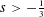$s>-\frac{1}{3}$, by establishing an energy estimate for the difference of two solutions with the same initial condition. For this purpose, we perform an infinite iteration of normal form reductions on the 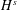$H^{s}$-energy functional, allowing us to introduce an infinite sequence of correction terms to the 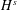$H^{s}$-energy functional in the spirit of the 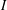$I$-method. In fact, the main novelty of this paper is this reduction of the 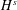$H^{s}$-energy functionals (for a single solution and for the difference of two solutions with the same initial condition) to sums of infinite series of multilinear terms of increasing degrees.

We consider smooth, complex quasiprojective varieties $U$ that admit a compactification with a boundary, which is an arrangement of smooth algebraic hypersurfaces. If the hypersurfaces intersect locally like hyperplanes, and the relative interiors of the hypersurfaces are Stein manifolds, we prove that the cohomology of certain local systems on $U$ vanishes. As an application, we show that complements of linear, toric, and elliptic arrangements are both duality and abelian duality spaces.

We prove that any cyclic quadrilateral can be inscribed in any closed convex $C^{1}$-curve. The smoothness condition is not required if the quadrilateral is a rectangle.

When $p>2$, we construct a Hodge-type analogue of Rapoport–Zink spaces under the unramifiedness assumption, as formal schemes parametrizing ‘deformations’ (up to quasi-isogeny) of $p$-divisible groups with certain crystalline Tate tensors. We also define natural rigid analytic towers with expected extra structure, providing more examples of ‘local Shimura varieties’ conjectured by Rapoport and Viehmann.

We consider the global behaviour for large solutions of the Dirac–Klein–Gordon system in critical spaces in dimension $1+3$. In particular, we show that bounded solutions exist globally in time and scatter, provided that a controlling space–time Lebesgue norm is finite. A crucial step is to prove nonlinear estimates that exploit the dichotomy between transversality and null structure, and furthermore involve the controlling norm.

We study logarithmically averaged binary correlations of bounded multiplicative functions $g_{1}$ and $g_{2}$. A breakthrough on these correlations was made by Tao, who showed that the correlation average is negligibly small whenever $g_{1}$ or $g_{2}$ does not pretend to be any twisted Dirichlet character, in the sense of the pretentious distance for multiplicative functions. We consider a wider class of real-valued multiplicative functions $g_{j}$, namely those that are uniformly distributed in arithmetic progressions to fixed moduli. Under this assumption, we obtain a discorrelation estimate, showing that the correlation of $g_{1}$ and $g_{2}$ is asymptotic to the product of their mean values. We derive several applications, first showing that the numbers of large prime factors of $n$ and $n+1$ are independent of each other with respect to logarithmic density. Secondly, we prove a logarithmic version of the conjecture of Erdős and Pomerance on two consecutive smooth numbers. Thirdly, we show that if $Q$ is cube-free and belongs to the Burgess regime $Q\leqslant x^{4-\unicode[STIX]{x1D700}}$, the logarithmic average around $x$ of the real character $\unicode[STIX]{x1D712}\hspace{0.6em}({\rm mod}\hspace{0.2em}Q)$ over the values of a reducible quadratic polynomial is small.

We introduce a path theoretic framework for understanding the representation theory of (quantum) symmetric and general linear groups and their higher-level generalizations over fields of arbitrary characteristic. Our first main result is a ‘super-strong linkage principle’ which provides degree-wise upper bounds for graded decomposition numbers (this is new even in the case of symmetric groups). Next, we generalize the notion of homomorphisms between Weyl/Specht modules which are ‘generically’ placed (within the associated alcove geometries) to cyclotomic Hecke and diagrammatic Cherednik algebras. Finally, we provide evidence for a higher-level analogue of the classical Lusztig conjecture over fields of sufficiently large characteristic.

In this paper we study the singularities of the invariant metric of the Poincaré bundle over a family of abelian varieties and their duals over a base of arbitrary dimension. As an application of this study we prove the effectiveness of the height jump divisors for families of pointed abelian varieties. The effectiveness of the height jump divisor was conjectured by Hain in the more general case of variations of polarized Hodge structures of weight  $-1$ .

We present a heuristic argument based on Honda–Tate theory against many conjectures in ‘unlikely intersections’ over the algebraic closure of a finite field; notably, we conjecture that every abelian variety of dimension 4 is isogenous to a Jacobian. Using methods of additive combinatorics, we answer a related question of Chai and Oort where the ambient Shimura variety is a power of the modular curve.

We obtain partial improvement toward the pointwise convergence problem of Schrödinger solutions, in the general setting of fractal measure. In particular, we show that, for $n\geqslant 3$, $\lim _{t\rightarrow 0}e^{it\unicode[STIX]{x1D6E5}}f(x)$$=f(x)$ almost everywhere with respect to Lebesgue measure for all $f\in H^{s}(\mathbb{R}^{n})$ provided that $s>(n+1)/2(n+2)$. The proof uses linear refined Strichartz estimates. We also prove a multilinear refined Strichartz using decoupling and multilinear Kakeya.

Let $f$ and $g$ be 1-bounded multiplicative functions for which $f\ast g=1_{.=1}$. The Bombieri–Vinogradov theorem holds for both $f$ and $g$ if and only if the Siegel–Walfisz criterion holds for both $f$ and $g$, and the Bombieri–Vinogradov theorem holds for $f$ restricted to the primes.

We show that the integral canonical models of Hodge-type Shimura varieties at odd good reduction primes admits ‘$p$-adic uniformization’ by Rapoport–Zink spaces of Hodge type constructed in Kim [Forum Math. Sigma6 (2018) e8, 110 MR 3812116].

We study the chromatic number of the curve graph of a surface. We show that the chromatic number grows like $k\log k$ for the graph of separating curves on a surface of Euler characteristic $-k$. We also show that the graph of curves that represent a fixed nonzero homology class is uniquely $t$-colorable, where $t$ denotes its clique number. Together, these results lead to the best known bounds on the chromatic number of the curve graph. We also study variations for arc graphs and obtain exact results for surfaces of low complexity. Our investigation leads to connections with Kneser graphs, the Johnson homomorphism, and hyperbolic geometry.

We study several kinds of subschemes of mixed characteristic models of Shimura varieties which admit good (partial) toroidal and minimal compactifications, with familiar boundary stratifications and formal local structures, as if they were Shimura varieties in characteristic zero. We also generalize Koecher’s principle and the relative vanishing of subcanonical extensions for coherent sheaves, and Pink’s and Morel’s formulas for étale sheaves, to the context of such subschemes.

Let $\mathbf{f}=(f_{1},\ldots ,f_{R})$ be a system of polynomials with integer coefficients in which the degrees need not all be the same. We provide sufficient conditions for which the system of equations $f_{j}(x_{1},\ldots ,x_{n})=0~(1\leqslant j\leqslant R)$ satisfies a general local to global type statement, and has a solution where each coordinate is prime. In fact we obtain the asymptotic formula for number of such solutions, counted with a logarithmic weight, under these conditions. We prove the statement via the Hardy–Littlewood circle method. This is a generalization of the work of Cook and Magyar [‘Diophantine equations in the primes’, Invent. Math.198 (2014), 701–737], where they obtained the result when the polynomials of $\mathbf{f}$ all have the same degree. Hitherto, results of this type for systems of polynomial equations involving different degrees have been restricted to the diagonal case.

This paper is dedicated to a problem raised by Jacquet Tits in 1956: the Weyl group of a Chevalley group should find an interpretation as a group over what is nowadays called $\mathbb{F}_{1}$, the field with one element. Based on Part I of The geometry of blueprints, we introduce the class of Tits morphisms between blue schemes. The resulting Tits category$\text{Sch}_{{\mathcal{T}}}$ comes together with a base extension to (semiring) schemes and the so-called Weyl extension to sets. We prove for ${\mathcal{G}}$ in a wide class of Chevalley groups—which includes the special and general linear groups, symplectic and special orthogonal groups, and all types of adjoint groups—that a linear representation of ${\mathcal{G}}$ defines a model $G$ in $\text{Sch}_{{\mathcal{T}}}$ whose Weyl extension is the Weyl group $W$ of ${\mathcal{G}}$. We call such models Tits–Weyl models. The potential of Tits–Weyl models lies in (a) their intrinsic definition that is given by a linear representation; (b) the (yet to be formulated) unified approach towards thick and thin geometries; and (c) the extension of a Chevalley group to a functor on blueprints, which makes it, in particular, possible to consider Chevalley groups over semirings. This opens applications to idempotent analysis and tropical geometry.