Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T22:23:05.733Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GEOMETRY OF BLUEPRINTS PART II: TITS–WEYL MODELS OF ALGEBRAIC GROUPS

Part of: Semigroups Generalizations Algebraic geometry: Foundations Algebraic groups

Published online by Cambridge University Press:  23 October 2018

OLIVER LORSCHEID
OLIVER LORSCHEID*
Affiliation:
Instituto Nacional de Matemática Pura e Aplicada, Rio de Janeiro, Brazil; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is dedicated to a problem raised by Jacquet Tits in 1956: the Weyl group of a Chevalley group should find an interpretation as a group over what is nowadays called 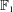$\mathbb{F}_{1}$, the field with one element. Based on Part I of The geometry of blueprints, we introduce the class of Tits morphisms between blue schemes. The resulting Tits category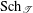$\text{Sch}_{{\mathcal{T}}}$ comes together with a base extension to (semiring) schemes and the so-called Weyl extension to sets. We prove for 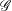${\mathcal{G}}$ in a wide class of Chevalley groups—which includes the special and general linear groups, symplectic and special orthogonal groups, and all types of adjoint groups—that a linear representation of 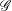${\mathcal{G}}$ defines a model 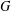$G$ in 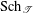$\text{Sch}_{{\mathcal{T}}}$ whose Weyl extension is the Weyl group 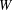$W$ of 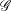${\mathcal{G}}$. We call such models Tits–Weyl models. The potential of Tits–Weyl models lies in (a) their intrinsic definition that is given by a linear representation; (b) the (yet to be formulated) unified approach towards thick and thin geometries; and (c) the extension of a Chevalley group to a functor on blueprints, which makes it, in particular, possible to consider Chevalley groups over semirings. This opens applications to idempotent analysis and tropical geometry.

MSC classification

Primary: 14A20: Generalizations (algebraic spaces, stacks) 14L15: Group schemes 14L35: Classical groups (geometric aspects) 16Y60: Semirings 20M14: Commutative semigroups
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e20
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2018

References

Artin, M., Bertin, J. E., Demazure, M., Gabriel, P., Grothendieck, A., Raynaud, M. and Serre, and J.-P., Schémas en groupes. I: Propriétés générales des schémas en groupes, Lecture Notes in Mathematics, 151 (Springer, Berlin, 1962/64).Google Scholar
Artin, M., Bertin, J. E., Demazure, M., Gabriel, P., Grothendieck, A., Raynaud, M. and Serre, J.-P., Schémas en groupes. II: Groupes de Type Multiplicatif, et Structure des Schémas en Groupes Généraux, Lecture Notes in Mathematics, 152 (Springer, Berlin, 1962/64).Google Scholar
Artin, M., Bertin, J. E., Demazure, M., Gabriel, P., Grothendieck, A., Raynaud, M. and Serre, J.-P., Schémas en groupes. III: Structure des schémas en groupes réductifs, Lecture Notes in Mathematics, 153 (Springer, Berlin, 1962/64).Google Scholar
Berkovich, V. G., ‘Étale cohomology for non-Archimedean analytic spaces’, Publ. Math. Inst. Hautes Études Sci. (78) (1994), 5–161, 1993.Google Scholar
Berkovich, V. G., ‘ p-adic analytic spaces’, inProceedings of the International Congress of Mathematicians (Berlin, 1998), Vol. II (1998), 141–151, number Extra Vol. II (electronic).Google Scholar
Borger, J., ‘ $\unicode[STIX]{x1D6EC}$ -rings and the field with one element’. Preprint, 2009, arXiv:0906.3146.Google Scholar
Carter, R. W., Simple Groups of Lie Type, Pure and Applied Mathematics, 28 (John Wiley & Sons, London–New York–Sydney, 1972).Google Scholar
Chevalley, C., ‘Sur certains groupes simples’, Tohoku Math. J. Second Series(7) (1955), 14–66.Google Scholar
Chevalley, C., ‘Certain schémas de groupes semi-simples’, Sem. Bourbaki (219) (1960/61), 219–234.Google Scholar
Connes, A. and Consani, C., ‘Characteristic 1, entropy and the absolute point’, inNoncommutative Geometry, Arithmetic, and Related Topics (Johns Hopkins University Press, Baltimore, MD, 2011), 75–139.Google Scholar
Connes, A. and Consani, C., ‘On the notion of geometry over F1 ’, J. Algebraic Geom. 20(3) (2011), 525–557.Google Scholar
Conrad, B., Reductive Group Schemes, Lecture Notes from the Summer School ‘Group schemes’ in Luminy (2011), http://math.stanford.edu/∼conrad/papers/luminysga3.pdf.Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive Groups, New Mathematical Monographs, 17 (Cambridge University Press, Cambridge, 2010).Google Scholar
Cortiñas, G., Haesemeyer, C., Mark, E., Walker, E. and Weibel, C., ‘Toric varieties, monoid schemes and cdh descent’. Preprint, 2011, arXiv:1106.1389v1.Google Scholar
Deitmar, A., ‘Schemes over F1 ’, inNumber Fields and Function Fields—Two Parallel Worlds, Progress in Mathematics, 239 (Birkhäuser Boston, Boston, MA, 2005), 87–100.Google Scholar
Deitmar, A., ‘Congruence schemes’. Preprint, 2011, arXiv:1102.4046.Google Scholar
Demazure, M. and Gabriel, P., Groupes algébriques (North-Holland Publishing Company, Amsterdam, 1970).Google Scholar
Gathmann, A., ‘Tropical algebraic geometry’, Jahresber. Dtsch. Math.-Ver. 108(1) (2006), 3–32.Google Scholar
Haran, M. J. S., ‘Non-additive geometry’, Compos. Math. 143 (2007), 618–688.Google Scholar
Huber, R., Étale Cohomology of Rigid Analytic Varieties and Adic Spaces, Aspects of Mathematics, E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).Google Scholar
Kapranov, M. and Smirnov, A., ‘Cohomology determinants and reciprocity laws: number field case’. Unpublished preprint.Google Scholar
Lescot, P., ‘Algèbre absolue’, Ann. Sci. Math. Québec 33(1) (2009), 63–82.Google Scholar
Lorscheid, O., ‘Algebraic groups over the field with one element’, Math. Z. 271(1–2) (2012), 117–138.Google Scholar
Lorscheid, O., ‘The geometry of blueprints. Part I: algebraic background and scheme theory’, Adv. Math. 229(3) (2012), 1804–1846.Google Scholar
Manin, Y., ‘Lectures on zeta functions and motives (according to Deninger and Kurokawa)’, Astérisque 4(228) (1995), 121–163. Columbia University Number Theory Seminar (New York, 1992).Google Scholar
Maslov, V. P. and Kolokol’tsov, V. N., Idempotent analysis and its Application to Optimal control (VO ‘Nauka’, Moscow, 1994) (in Russian).Google Scholar
Mikhalkin, G., ‘Tropical geometry and its applications’, inInternational Congress of Mathematicians, Vol. II (European Mathematical Society, Zürich, 2006), 827–852.Google Scholar
Mikhalkin, G., ‘Tropical geometry’. Unpublished notes, 2010.Google Scholar
Paugam, F., ‘Global analytic geometry’, J. Number Theory 129(10) (2009), 2295–2327.Google Scholar
Peña, J. L. and Lorscheid, O., ‘Torified varieties and their geometries over F 1 ’, Math. Z. 267(3) (2011), 605–643.Google Scholar
Soulé, C., ‘Les variétés sur le corps à un élément’, Mosc. Math. J. 4(1) (2004), 217–244, 312.Google Scholar
Takagi, S., ‘Construction of schemes over $\mathbb{F}_{1}$ , and over idempotent semirings: towards tropical geometry’. Preprint, 2010, arXiv:1009.0121.Google Scholar
Tits, J., ‘Sur les analogues algébriques des groupes semi-simples complexes’, inColloque d’algèbre supérieure, tenu à Bruxelles du 19 au 22 décembre 1956, Centre Belge de Recherches Mathématiques (Établissements Ceuterick, Louvain, 1957), 261–289.Google Scholar
Tits, J., ‘Normalisateurs de tores. I. Groupes de Coxeter étendus’, J. Algebra 4 (1966), 96–116.Google Scholar
Toën, B. and Vaquié, M., ‘Au-dessous de Spec ℤ’, J. K-Theory 3(3) (2009), 437–500.Google Scholar