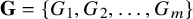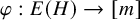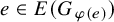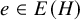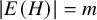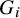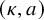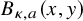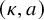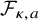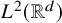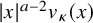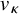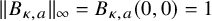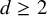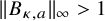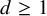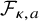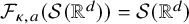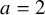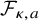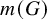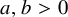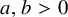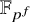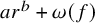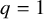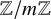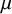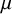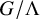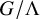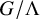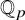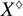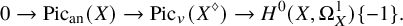15 results in Most Downloaded Articles
Double Schubert polynomials do have saturated Newton polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2023, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rainbow spanning structures in graph and hypergraph systems
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2023, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rigorous derivation of the Hamiltonian structure for the Vlasov equation
- Part of:
-
- Published online by Cambridge University Press:
- 05 September 2023, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for evolutionary partial differential equations in classical function spaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the kernel of the
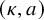 $(\kappa ,a)$-Generalized fourier transform
$(\kappa ,a)$-Generalized fourier transform
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2023, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The maximal size of a minimal generating set
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2023, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remixed Eulerian numbers
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2023, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the class of all the rings
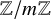 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expanding measures: Random walks and rigidity on homogeneous spaces
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2023, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heights on stacks and a generalized Batyrev–Manin–Malle conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Line bundles on rigid spaces in the v-topology
- Part of:
-
- Published online by Cambridge University Press:
- 22 September 2022, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categorical traces and a relative Lefschetz–Verdier formula
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2022, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BREAKING THE COHERENCE BARRIER: A NEW THEORY FOR COMPRESSED SENSING
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation