Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T23:05:59.020Z Has data issue: false hasContentIssue false
  • English
  • Français

TILING DIRECTED GRAPHS WITH TOURNAMENTS

Published online by Cambridge University Press:  14 February 2018

ANDRZEJ CZYGRINOW ,
LOUIS DEBIASIO ,
THEODORE MOLLA  and
ANDREW TREGLOWN
ANDRZEJ CZYGRINOW
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, AZ 85281, USA; [email protected]
LOUIS DEBIASIO
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA; [email protected]
THEODORE MOLLA
Affiliation:
Department of Mathematics and Statistics, University of South Florida, Tampa, FL 33620, USA; [email protected]
ANDREW TREGLOWN
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Hajnal–Szemerédi theorem states that for any positive integer $r$ and any multiple $n$ of $r$, if 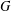$G$ is a graph on $n$ vertices and 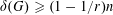$\unicode[STIX]{x1D6FF}(G)\geqslant (1-1/r)n$, then 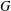$G$ can be partitioned into 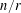$n/r$ vertex-disjoint copies of the complete graph on $r$ vertices. We prove a very general analogue of this result for directed graphs: for any positive integer $r$ with 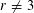$r\neq 3$ and any sufficiently large multiple $n$ of $r$, if 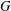$G$ is a directed graph on $n$ vertices and every vertex is incident to at least 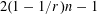$2(1-1/r)n-1$ directed edges, then 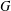$G$ can be partitioned into 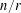$n/r$ vertex-disjoint subgraphs of size $r$ each of which contain every tournament on $r$ vertices (the case 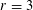$r=3$ is different and was handled previously). In fact, this result is a consequence of a tiling result for standard multigraphs (that is multigraphs where there are at most two edges between any pair of vertices). A related Turán-type result is also proven.

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e2
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Alon, N. and Yuster, R., ‘Almost H-factors in dense graphs’, Graphs Combin. 8 (1992), 95–102.Google Scholar
Balogh, J., Lo, A. and Molla, T., ‘Transitive triangle tilings in oriented graphs’, J. Combin. Theory B 124 (2017), 64–87.Google Scholar
Benevides, F. S., Łuczak, T., Scott, A., Skokan, J. and White, M., ‘Monochromatic cycles in 2-coloured graphs’, Combin. Probab. Comput. 21 (2012), 57–87.Google Scholar
Brown, W. G. and Harary, F., ‘Extremal digraphs’, Coll. Math. Soc. J. Bolyai 4 (1969), 135–198.Google Scholar
Corrádi, K. and Hajnal, A., ‘On the maximal number of independent circuits in a graph’, Acta Math. Acad. Sci. Hungar. 14 (1964), 423–439.Google Scholar
Czygrinow, A., DeBiasio, L., Kierstead, H. A. and Molla, T., ‘An extension of the Hajnal–Szemerédi theorem to directed graphs’, Combin. Probab. Comput. 24 (2015), 754–773.Google Scholar
Czygrinow, A., Kierstead, H. A. and Molla, T., ‘On directed versions of the Corrádi–Hajnal Corollary’, European J. Combin. 42 (2014), 1–14.CrossRefGoogle Scholar
Grosu, C. and Hladký, J., ‘The extremal function for partial bipartite tilings’, European J. Combin. 33 (2012), 807–815.Google Scholar
Hajnal, A. and Szemerédi, E., ‘Proof of a conjecture of Erdős’, inCombinatorial Theory and its Applications II, (eds. Erdős, P., Rényi, A. and Sos, V. T.) Colloq. Math. Soc. J. Bolyai 4 (North-Holland, Amsterdam, 1970), 601–623.Google Scholar
Havet, F. and Thomassé, S., ‘Oriented hamiltonian paths in tournaments: A proof of Rosenfeld’s conjecture’, J.  Combin. Theory B 78 (2000), 243–273.Google Scholar
Hell, P. and Kirkpatrick, D. G., ‘On the complexity of general graph factor problems’, SIAM J. Comput. 12 (1983), 601–609.Google Scholar
Keevash, P. and Mycroft, R., ‘A multipartite Hajnal–Szemerédi theorem’, J. Combin. Theory B 114 (2015), 187–236.CrossRefGoogle Scholar
Keevash, P. and Sudakov, B., ‘Triangle packings and 1-factors in oriented graphs’, J. Combin. Theory B 99 (2009), 709–727.Google Scholar
Kierstead, H. A. and Kostochka, A. V., ‘An Ore-type theorem on equitable coloring’, J. Combin. Theory B 98 (2008), 226–234.CrossRefGoogle Scholar
Kierstead, H. A. and Kostochka, A. V., ‘A short proof of the Hajnal–Szemerédi theorem on equitable coloring’, Combin. Probab. Comput. 17 (2008), 265–270.CrossRefGoogle Scholar
Komlós, J., ‘Tiling Turán theorems’, Combinatorica 20 (2000), 203–218.Google Scholar
Komlós, J., Sárközy, G. and Szemerédi, E., ‘Proof of the Alon–Yuster conjecture’, Discrete Math. 235 (2001), 255–269.Google Scholar
Komlós, J. and Simonovits, M., ‘Szemerédi’s Regularity Lemma and its applications in graph theory’, inCombinatorics, Paul Erdős is Eighty II, (eds. Miklós, D., Sós, V. T. and Szőnyi, T.) Bolyai Society Studies 2 (Budapest, 1996), 295–352.Google Scholar
Kühn, D. and Osthus, D., ‘Critical chromatic number and the complexity of perfect packings in graphs’, in17th ACM-SIAM Symposium on Discrete Algorithms (SODA, 2006), 851–859.Google Scholar
Kühn, D. and Osthus, D., ‘The minimum degree threshold for perfect graph packings’, Combinatorica 29 (2009), 65–107.CrossRefGoogle Scholar
Kühn, D. and Osthus, D., ‘Embedding large subgraphs into dense graphs’, inSurveys in Combinatorics, (eds. Huczynska, S., Mitchell, J. D. and Roney-Dougal, C. M.) London Mathematical Society Lecture Note Series, 365 (Cambridge University Press, Cambridge, 2009), 137–167.Google Scholar
Lo, A. and Markström, K., ‘ F-factors in hypergraphs via absorption’, Graphs Combin. 31 (2015), 679–712.CrossRefGoogle Scholar
Molla, T., ‘Tiling directed graphs with cycles and tournaments’, PhD Thesis, Arizona State University, Tempe, Arizona, 2013.Google Scholar
Rödl, V., Ruciński, A. and Szemerédi, E., ‘A Dirac-type theorem for 3-uniform hypergraphs’, Combin. Probab. Comput. 15 (2006), 229–251.Google Scholar
Szemerédi, E., ‘Regular partitions of graphs’, inProblémes Combinatoires et Théorie des Graphes, Colloques Internationaux CNRS, 260 (Univ. Orsay, Orsay, 1976), 399–401.Google Scholar
Treglown, A., ‘A note on some oriented graph embedding problems’, J. Graph Theory 69 (2012), 330–336.CrossRefGoogle Scholar
Treglown, A., ‘On directed versions of the Hajnal–Szemerédi theorem’, Combin. Probab. Comput. 24 (2015), 873–928.CrossRefGoogle Scholar
Treglown, A., ‘A degree sequence Hajnal-Szemerédi theorem’, J. Combin. Theory B 118 (2016), 13–43.Google Scholar
Wang, H., ‘Independent directed triangles in a directed graph’, Graphs Combin. 16 (2000), 453–462.Google Scholar
Yuster, R., ‘Tiling transitive tournaments and their blow-ups’, Order 20 (2003), 121–133.CrossRefGoogle Scholar
Zhao, Y., ‘Recent advances on Dirac-type problems for hypergraphs’, inRecent Trends in Combinatorics, The IMA Volumes in Mathematics and its Applications, 159 (Springer, New York, 2015), Vii 706.Google Scholar