Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T22:46:47.563Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIME SOLUTIONS TO POLYNOMIAL EQUATIONS IN MANY VARIABLES AND DIFFERING DEGREES

Part of: Additive number theory; partitions Diophantine equations

Published online by Cambridge University Press:  18 October 2018

SHUNTARO YAMAGISHI
SHUNTARO YAMAGISHI*
Affiliation:
Department of Mathematics and Statistics, Queen’s University, Kingston, Ontario K7L 3N6, Canada; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 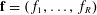$\mathbf{f}=(f_{1},\ldots ,f_{R})$ be a system of polynomials with integer coefficients in which the degrees need not all be the same. We provide sufficient conditions for which the system of equations 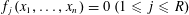$f_{j}(x_{1},\ldots ,x_{n})=0~(1\leqslant j\leqslant R)$ satisfies a general local to global type statement, and has a solution where each coordinate is prime. In fact we obtain the asymptotic formula for number of such solutions, counted with a logarithmic weight, under these conditions. We prove the statement via the Hardy–Littlewood circle method. This is a generalization of the work of Cook and Magyar [‘Diophantine equations in the primes’, Invent. Math.198 (2014), 701–737], where they obtained the result when the polynomials of 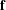$\mathbf{f}$ all have the same degree. Hitherto, results of this type for systems of polynomial equations involving different degrees have been restricted to the diagonal case.

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes 11P55: Applications of the Hardy-Littlewood method
Secondary: 11D45: Counting solutions of Diophantine equations 11D72: Equations in many variables
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e19
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits noncommercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author 2018

References

Birch, B. J., ‘Forms in many variables’, Proc. R. Soc. Lond. Ser. A 265 (1961/62), 245–263.Google Scholar
Bourgain, J., Gamburd, A. and Sarnak, P., ‘Affine linear sieve, expanders, and sum-product’, Invent. Math. 179(3) (2010), 559–644.Google Scholar
Browning, T. D. and Heath-Brown, D. R., ‘Forms in many variables and differing degrees’, J. Eur. Math. Soc. (JEMS) 9 (2017), 357–394.Google Scholar
Brüdern, J., Dietmann, R., Liu, J. and Wooley, T. D., ‘A Birch–Goldbach theorem’, Arch. Math. (Basel) 94(1) (2010), 53–58.Google Scholar
Chow, S., ‘Roth-Waring-Goldbach’, Int. Math. Res. Not. IMRN 2018(8) (2018), 2341–2374.Google Scholar
Cook, B. and Magyar, Á., ‘Diophantine equations in the primes’, Invent. Math. 198 (2014), 701–737.Google Scholar
Davenport, H., Analytic Methods for Diophantine Equations and Diopantine Inequalities, 2nd edn (Cambridge University Press, Cambridge, 2005).Google Scholar
Duke, W., Rudnick, Z. and Sarnak, P., ‘Density of integer points on affine homogeneous varieties’, Duke Math. J. 71(1) (1993), 143–179.Google Scholar
Goldston, D. A., Pintz, J. and Yıldırım, C. Y., ‘Primes in tuples. I’, Ann. of Math. (2) 170(2) (2009), 819–862.Google Scholar
Green, B. and Tao, T., ‘The primes contain arbitrarily long arithmetic progressions’, Ann. of Math. (2) 167(2) (2008), 481–547.Google Scholar
Green, B. and Tao, T., ‘The distribution of polynomials over finite fields, with applications to the Gowers norms’, Contrib. Discrete Math. 4(2) (2009), 1–36.Google Scholar
Green, B. and Tao, T., ‘Linear equations in primes’, Ann. of Math. (2) 171(3) (2010), 1753–1850.Google Scholar
Helfgott, H. A., ‘The ternary Goldbach problem’, Ann. Math. Stud., to appear.Google Scholar
Hua, L. K., Additive Theory of Prime Numbers, Translations of Mathematical Monographs, 13 (American Mathematical Society, Providence, RI, 1965).Google Scholar
Kaufman, T. and Lovett, S., ‘Worst case to average case reductions for polynomials’, in49th Annual IEEE Symposium on Foundations of Computer Science (2008), 166–175. https://www.computer.org/csdl/proceedings/focs/2008/3436/00/3436a166-abs.html.Google Scholar
Kumchev, A. V. and Wooley, T. D., ‘On the Waring-Goldbach problem for eighth and higher powers’, J. Lond. Math. Soc. (2) 93(3) (2016), 811–824.Google Scholar
Kumchev, A. V. and Wooley, T. D., ‘On the Waring-Goldbach problem for seventh and higher powers’, Monatsh. Math. 183(2) (2017), 303–310.Google Scholar
Liu, J. and Sarnak, P., ‘Integral points on quadrics in three variables whose coordinates have few prime factors’, Israel J. Math. 178 (2010), 393–426.Google Scholar
Maynard, J., ‘Small gaps between primes’, Ann. of Math. (2) 181(1) (2015), 383–413.Google Scholar
Schmidt, W. M., ‘The density of integer points on homogeneous varieties’, Acta Math. 154(3–4) (1985), 243–296.Google Scholar
Vinogradov, I. M., ‘Representation of an odd number as a sum of three primes’, Dokl. Akad. Nauk. SSSR 15 (1937), 291–294.Google Scholar
Xiao, S. Y. and Yamagishi, S., ‘Zeroes of polynomials in many variables with prime inputs’. Preprint, 2015, arXiv:1512.01258.Google Scholar
Yamagishi, S., ‘An exponential sum estimate for systems with linear polynomials’, J. Théor. Nombres Bordeaux, to appear.Google Scholar
Zhang, Y., ‘Bounded gaps between primes’, Ann. of Math. (2) 179(3) (2014), 1121–1174.Google Scholar
Zhao, L., ‘The quadratic form in nine prime variables’, Nagoya Math. J. 223(1) (2016), 21–65.Google Scholar