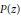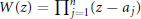Let $P\left( z \right)$ be a polynomial of degree not exceeding $n$ and let $W\left( z \right)\,=\,\prod\nolimits_{j=1}^{n}{\left( z\,-\,{{a}_{j}} \right)}$ where 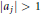$\left| {{a}_{j}} \right|\,>\,1$, 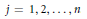$j\,=\,1,\,2,\,.\,.\,.\,,\,n$. If the rational function 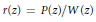$r\left( z \right)\,=\,{P\left( z \right)}/{W\left( z \right)}\;$ does not vanish in 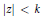$\left| z \right|\,<\,k$, then for 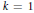$k\,=\,1$ it is known that

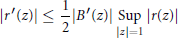$$\left| {{r}^{'}}\left( z \right) \right|\le \frac{1}{2}\left| {{B}^{'}}(z) \right|_{\left| z \right|=1}^{\text{Sup}}\left| r(z) \right|$$

where 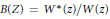$B\left( Z \right)\,=\,{{{W}^{*}}\left( z \right)}/{W\left( z \right)}\;$ and ${{W}^{*}}\left( z \right)\,=\,{{z}^{n}}\overline{W\left( {1}/{\overline{z}}\; \right)}$. In the paper we consider the case when $k\,>\,1$ and obtain a sharp result. We also show that

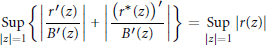$$\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left\{ \left| \frac{{{r}^{\prime }}\left( z \right)}{{{B}^{\prime }}\left( z \right)} \right|+\left| \frac{{{\left( {{r}^{*}}\left( z \right) \right)}^{\prime }}}{{{B}^{\prime }}\left( z \right)} \right| \right\}=\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left| r\left( z \right) \right|$$

where 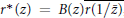${{r}^{*}}\left( z \right)\,=\,B\left( z \right)\overline{r\left( {1}/{\overline{z}}\; \right)}$, and as a consquence of this result, we present a generalization of a theorem of O’Hara and Rodriguez for self-inversive polynomials. Finally, we establish a similar result when supremum is replaced by infimum for a rational function which has all its zeros in the unit circle.

A well-known result, due to Ostrowski, states that if ${{\left\| P-Q \right\|}_{2}}\,<\,\varepsilon $, then the roots $({{x}_{j}})$ of $P$ and $({{y}_{j}})$ of $Q$ satisfy $\left| {{x}_{j}}\,-\,{{y}_{j}} \right|\,\le \,Cn{{\varepsilon }^{1/n}}$, where $n$ is the degree of $P$ and $Q$. Though there are cases where this estimate is sharp, it can still be made more precise in general, in two ways: first by using Bombieri’s norm instead of the classical ${{l}_{1}}$ or ${{l}_{2}}$ norms, and second by taking into account the multiplicity of each root. For instance, if $x$ is a simple root of $P$, we show that $\left| x\,-\,y \right|\,<\,C\varepsilon $ instead of ${{\varepsilon }^{1/n}}$. The proof uses the properties of Bombieri’s scalar product andWalsh Contraction Principle.

Any knot in a 3-dimensional homology sphere is homotopic to a knot with trivial Alexander polynomial.

Hecke operators are used to investigate part of the ${{E}_{2}}$-term of the Adams spectral sequence based on elliptic homology. The main result is a derivation of $\text{Ex}{{\text{t}}^{1}}$ which combines use of classical Hecke operators and $p$-adic Hecke operators due to Serre.

We define generalized Mellin transforms of mixed cusp forms, show their convergence, and prove that the function obtained by such a Mellin transform of a mixed cusp form satisfies a certain functional equation. We also prove that a mixed cusp form can be identified with a holomorphic form of the highest degree on an elliptic variety.

A new infinite product ${{t}_{n}}$ was introduced by S. Ramanujan on the last page of his third notebook. In this paper, we prove Ramanujan’s assertions about ${{t}_{n}}$ by establishing new connections between the modular $j$-invariant and Ramanujan’s cubic theory of elliptic functions to alternative bases. We also show that for certain integers $n$, ${{t}_{n}}$ generates the Hilbert class field of $\mathbb{Q}\left( \sqrt{-n} \right)$. This shows that ${{t}_{n}}$ is a new class invariant according to H. Weber’s definition of class invariants.

A $Q$-set is a set of reals every subset of which is a relative ${{G}_{\delta }}$. We investigate the combinatorics of $Q$-sets and discuss a question of Miller and Zhou on the size $q$ of the smallest set of reals which is not a $Q$-set. We show in particular that various natural lower bounds for $q$ are consistently strictly smaller than $q$.

Every weakly compact composition operator between weighted Banach spaces $H_{v}^{\infty }$ of analytic functions with weighted sup-norms is compact. Lower and upper estimates of the essential norm of continuous composition operators are obtained. The norms of the point evaluation functionals on the Banach space $H_{v}^{\infty }$ are also estimated, thus permitting to get new characterizations of compact composition operators between these spaces.

Let $M$ be a compact, connected, orientable 3-manifold whose boundary is a torus and whose interior admits a complete hyperbolic metric of finite volume. In this paper we show that if theminimal Culler-Shalen norm of a non-zero class in ${{H}_{1}}(\partial M)$ is larger than 8, then the finite surgery conjecture holds for $M$. This means that there are at most 5 Dehn fillings of $M$ which can yieldmanifolds having cyclic or finite fundamental groups and the distance between any slopes yielding such manifolds is at most 3.

A sequence of positive rationals generates a subgroup of finite index in the multiplicative positive rationals, and group product representations by the sequence need only a bounded number of terms, if and only if certain related sequences have densities uniformly bounded from below.

Analogues of van der Waerden’s theorem on arithmetic progressions are considered where the family of all arithmetic progressions, $\text{AP}$, is replaced by some subfamily of $\text{AP}$. Specifically, we want to know for which sets $A$, of positive integers, the following statement holds: for all positive integers $r$ and $k$, there exists a positive integer $n={w}'\text{(}k,r)$ such that for every $r$-coloring of $[1,\,n]$ there exists a monochromatic $k$-term arithmetic progression whose common difference belongs to $A$. We will call any subset of the positive integers that has the above property large. A set having this property for a specific fixed $r$ will be called $r$-large. We give some necessary conditions for a set to be large, including the fact that every large set must contain an infinite number of multiples of each positive integer. Also, no large set $\{{{a}_{n}}\,:\,n\,=\,1,\,2,\ldots \}$ can have $\underset{n\to \infty }{\mathop{\lim \,\inf }}\,\,\frac{{{a}_{n+1}}}{{{a}_{n}}}\,>\,1$. Sufficient conditions for a set to be large are also given. We show that any set containing $n$-cubes for arbitrarily large $n$, is a large set. Results involving the connection between the notions of “large” and “2-large” are given. Several open questions and a conjecture are presented.

We construct two non-isomorphic nuclear, stably finite, real rank zero ${{C}^{*}}$-algebras $E$ and ${{E}^{'}}$ for which there is an isomorphism of ordered groups $\Theta :{{\oplus }_{n\ge 0}}{{K}_{\bullet }}(E;\mathbb{Z}/n)\to {{\oplus }_{n\ge 0}}{{K}_{\bullet }}({E}';\mathbb{Z}/n)$ which is compatible with all the coefficient transformations. The ${{C}^{*}}$-algebras $E$ and ${{E}^{'}}$ are not isomorphic since there is no $\Theta$ as above which is also compatible with the Bockstein operations. By tensoring with Cuntz’s algebra ${{\mathcal{O}}_{\infty }}$ one obtains a pair of non-isomorphic, real rank zero, purely infinite ${{C}^{*}}$-algebras with similar properties.

This paper contains two essentially independent results in the invariant theory of finite groups. First we prove that, for any faithful representation of a non-trivial $p$-group over a field of characteristic $p$, the ring of vector invariants of $m$ copies of that representation is not Cohen-Macaulay for $m\,\ge \,3$. In the second section of the paper we use Poincaré series methods to produce upper bounds for the degrees of the generators for the ring of invariants as long as that ring is Gorenstein. We prove that, for a finite non-trivial group $G$ and a faithful representation of dimension $n$ with $n\,>\,1$, if the ring of invariants is Gorenstein then the ring is generated in degrees less than or equal to $n(\left| G \right|\,-\,1)$. If the ring of invariants is a hypersurface, the upper bound can be improved to $\left| G \right|$.

Let $X$ be a compact nonsingular real algebraic variety and let $Y$ be either the blowup of ${{\mathbb{P}}^{n}}\left( \mathbb{R} \right)$ along a linear subspace or a nonsingular hypersurface of ${{\mathbb{P}}^{m}}\left( \mathbb{R} \right)\,\times \,{{\mathbb{P}}^{n}}\left( \mathbb{R} \right)$ of bidegree (1, 1). It is proved that a ${{\mathcal{C}}^{\infty }}$ map $f:\,X\,\to \,Y$ can be approximated by regular maps if and only if ${{f}^{*}}\left( {{H}^{1}}\left( Y,\,{\mathbb{Z}}/{2}\; \right) \right)\,\subseteq \,H_{a\lg }^{1}\left( X,\,{\mathbb{Z}}/{2}\; \right)$, where $H_{a\lg }^{1}\left( X,\,{\mathbb{Z}}/{2}\; \right)$ is the subgroup of ${{H}^{1}}\left( X,\,{\mathbb{Z}}/{2}\; \right)$ generated by the cohomology classes of algebraic hypersurfaces in $X$. This follows from another result on maps into generalized flag varieties.

In this paper we prove: for any positive integers $a$ and $q$ with $\left( a,\,q \right)\,=\,1$, we have uniformly

$$\sum\limits_{\begin{matrix} n\le N \\ (n,q)=1,n\bar{n}\equiv 1(\,\bmod \,q) \\ \end{matrix}}{\mu (n)e(\frac{a\bar{n}}{q})\ll Nd(q)\left\{ \frac{{{\log }^{\frac{5}{2}}}N}{{{q}^{\frac{1}{2}}}}+\frac{{{q}^{\frac{1}{5}}}{{\log }^{\frac{13}{5}}}N}{{{N}^{\frac{1}{5}}}} \right\}.}$$

This improves the previous bound obtained by D. Hajela, A. Pollington and B. Smith [5].

Recent work of Ding and Huang shows that if we perturb a bounded operator (between Hilbert spaces) which has closed range, then the perturbed operator again has closed range. We extend this result by introducing a weaker perturbation condition, and our result is then used to prove a theorem about the stability of frames for a subspace.

We investigate pointwise domination property in operator spaces generated by Lorentz sequence spaces.

Let $\text{Alg}\left( \mathcal{L} \right)$ be the algebra of all bounded linear operators on a normed linear space $\mathcal{X}$ leaving invariant each member of the complete lattice of closed subspaces $\mathcal{L}$. We discuss when the subalgebra of finite rank operators in $\text{Alg}\left( \mathcal{L} \right)$ is non-zero, and give an example which shows this subalgebra may be zero even for finite lattices. We then give a necessary and sufficient lattice condition for decomposing a finite rank operator $F$ into a sum of a rank one operator and an operator whose range is smaller than that of $F$, each of which lies in $\text{Alg}\left( \mathcal{L} \right)$. This unifies results of Erdos, Longstaff, Lambrou, and Spanoudakis. Finally, we use the existence of finite rank operators in certain algebras to characterize the spectra of Riesz operators (generalizing results of Ringrose and Clauss) and compute the Jacobson radical for closed algebras of Riesz operators and $\text{Alg}\left( \mathcal{L} \right)$ for various types of lattices.

It is shown that under $\text{ZFC}$ almost all planar compacta that meet every line in at most two points are subsets of sets that meet every line in exactly two points. This result was previously obtained by the author jointly with K. Kunen and J. vanMill under the assumption that Martin’s Axiom is valid.

We give a direct proof that the space of Baire quasi-measures on a completely regular space (or the space of Borel quasi-measures on a normal space) is compact Hausdorff. We show that it is possible for the space of Borel quasi-measures on a non-normal space to be non-compact. This result also provides an example of a Baire quasi-measure that has no extension to a Borel quasi-measure. Finally, we give a concise proof of the Wheeler-Shakmatov theorem, which states that if $X$ is normal and $\dim\left( X \right)\,\le \,1$, then every quasi-measure on $X$ extends to a measure.