Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T07:19:59.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Maps and Real Algebraic Morphisms

Published online by Cambridge University Press:  20 November 2018

J. Bochnak  and
W. Kucharz
J. Bochnak
Affiliation:
Department of Mathematics, Vrije Universiteit, De Boelelaan 1081a 1081 HV Amsterdam, The Netherlands, email: [email protected]
W. Kucharz
Affiliation:
University of New Mexico, Department of Mathematics and Statistics Albuquerque, NM 87131-1141 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 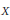$X$ be a compact nonsingular real algebraic variety and let 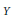$Y$ be either the blowup of 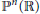${{\mathbb{P}}^{n}}\left( \mathbb{R} \right)$ along a linear subspace or a nonsingular hypersurface of 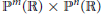${{\mathbb{P}}^{m}}\left( \mathbb{R} \right)\,\times \,{{\mathbb{P}}^{n}}\left( \mathbb{R} \right)$ of bidegree (1, 1). It is proved that a 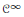${{\mathcal{C}}^{\infty }}$ map 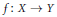$f:\,X\,\to \,Y$ can be approximated by regular maps if and only if ${{f}^{*}}\left( {{H}^{1}}\left( Y,\,{\mathbb{Z}}/{2}\; \right) \right)\,\subseteq \,H_{a\lg }^{1}\left( X,\,{\mathbb{Z}}/{2}\; \right)$, where 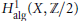$H_{a\lg }^{1}\left( X,\,{\mathbb{Z}}/{2}\; \right)$ is the subgroup of 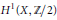${{H}^{1}}\left( X,\,{\mathbb{Z}}/{2}\; \right)$ generated by the cohomology classes of algebraic hypersurfaces in 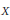$X$. This follows from another result on maps into generalized flag varieties.

Keywords

14P0514P25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 4 , 01 December 1999 , pp. 445 - 451
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Benedetti, R. and Tognoli, A., On real algebraic vector bundles. Bull. Sci. Math. (2) 104 (1980), 89–112.Google Scholar
[2] Bochnak, J., Coste, M. and Roy, M.-F., G´eom´etrie Alg´ebrique R´eelle. Ergeb. Math. Grenzgeb., Berlin-Heidelberg-New York, Springer, 1987.Google Scholar
[3] Bochnak, J. and Kucharz, W., Algebraic approximation of mappings into spheres. Michigan Math. J. 34 (1987), 119–125.Google Scholar
[4] Hirsch, M., Differential Topology. Berlin-Heidelberg-New York, Springer, 1976.Google Scholar
[5] Huisman, J., A real algebraic vector bundle is strongly algebraic whenever its total space is affine. In: Real Algebraic Geometry and Topology, ContemporaryMath. 182 (1995), 117–119.Google Scholar
[6] Kucharz, W., Real algebraic morphisms into flag varieties. Boll. Un. Mat. Ital. A (7) 8 (1994), 345–352.Google Scholar
[7] Kucharz, W. and Rusek, K., Approximation of smooth maps by real algebraic morphisms. Canad. Math. Bull. 40(1997), 456–463.Google Scholar