Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T04:12:12.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Rank Operators in Certain Algebras

Published online by Cambridge University Press:  20 November 2018

Sean Bradley
Sean Bradley*
Affiliation:
Department of Mathematics, Clarke College, Dubuque, Iowa 52001 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 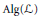$\text{Alg}\left( \mathcal{L} \right)$ be the algebra of all bounded linear operators on a normed linear space 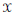$\mathcal{X}$ leaving invariant each member of the complete lattice of closed subspaces 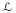$\mathcal{L}$. We discuss when the subalgebra of finite rank operators in 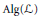$\text{Alg}\left( \mathcal{L} \right)$ is non-zero, and give an example which shows this subalgebra may be zero even for finite lattices. We then give a necessary and sufficient lattice condition for decomposing a finite rank operator 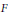$F$ into a sum of a rank one operator and an operator whose range is smaller than that of 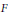$F$, each of which lies in 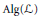$\text{Alg}\left( \mathcal{L} \right)$. This unifies results of Erdos, Longstaff, Lambrou, and Spanoudakis. Finally, we use the existence of finite rank operators in certain algebras to characterize the spectra of Riesz operators (generalizing results of Ringrose and Clauss) and compute the Jacobson radical for closed algebras of Riesz operators and 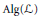$\text{Alg}\left( \mathcal{L} \right)$ for various types of lattices.

Keywords

47D3047A1547A10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 4 , 01 December 1999 , pp. 452 - 462
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Barnes, B. A. and Clauss, J. M., Spectral and Fredholm Properties of Operators in Elementary Nest Algebras. To appear.Google Scholar
[2] Barnes, B. A. and Katavolos, A., Properties of Quasinilpotents in Some Operator Algebras. Proc. Roy. Irish Acad. Sect. A (2) 93 (1993), 155–170.Google Scholar
[3] Clauss, J. M., Elementary Chains of Invariant Subspaces of a Banach Space. Canad. J. Math. (2) 47 (1995), 290–301.Google Scholar
[4] Dowson, H. R., Spectral Theory of Linear Operators. Academic Press, New York, 1978.Google Scholar
[5] Erdos, J. A., Operators of Finite Rank in Nest Algebras. J. LondonMath. Soc. 43 (1968), 391–397.Google Scholar
[6] Fillmore, P. A. and Williams, J. P., On Operator Ranges. Adv. Math. 7 (1971), 254–281.Google Scholar
[7] Gr¨atzer, G., Lattice Theory; First Concepts and Distributivity. Freeman, San Francisco, 1971.Google Scholar
[8] Halmos, P. R., Reflexive Lattices of Subspaces. J. LondonMath. Soc. (2) 4 (1971), 257–265.Google Scholar
[9] Hopenwasser, A. and Moore, R., Finite Rank Operators in Reflexive Operator Algebras. J. London Math. Soc. (2) 27 (1983), 331–338.Google Scholar
[10] Katavolos, A. and Katsoulis, E., Semisimplicity in Operator Algebras and Subspace Lattices. J. London Math. Soc. (2) 42 (1990), 365–372.Google Scholar
[11] Lambrou, M. S., Approximants, Commutants, and Double Commutants in Normed Algebras. J. LondonMath. Soc. (2) 25 (1982), 499–512.Google Scholar
[12] Longstaff, W. E., Remarks on Semi-simple Reflexive Algebras. Proc. Centre Math. Anal. Austral. Nat. Univ. 21, 1989, 273–287.Google Scholar
[13] Longstaff, W. E., Some Problems Concerning ReflexiveOperator Algebras. Proc. Centre Math. Anal. Austral.Nat. Univ. 21, 1989, 260–272.Google Scholar
[14] Longstaff, W. E., Strongly Reflexive Lattices. J. London Math. Soc. (2) 11 (1975), 491–498.Google Scholar
[15] Palmer, T. W., Banach Algebras and the General Theory of *-algebras. Volume I, Cambridge Univ. Press, New York, 1994.Google Scholar
[16] Ringrose, J. R., On Some Algebras of Operators. Proc. LondonMath. Soc. (3) 15 (1965), 61–83.Google Scholar
[17] Ringrose, J. R., Compact Non-Self-Adjoint Operators. Van Nostrand Rheinhold Company, Princeton, New Jersey, 1971.Google Scholar
[18] Spanoudakis, N. K., Generalizations of Certain Nest Algebra Results. Proc. Amer.Math. Soc. 115 (1992), 711–723.Google Scholar
[19] Spanoudakis, N. K., Finite Distributive Lattices. Preprint.Google Scholar