Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T02:04:59.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Non Cohen-Macaulay Vector Invariants and a Noether Bound for a Gorenstein Ring of Invariants

Published online by Cambridge University Press:  20 November 2018

H. E. A. Campbell ,
A. V. Geramita ,
I. P. Hughes ,
R. J. Shank  and
D. L. Wehlau
H. E. A. Campbell
Affiliation:
Department of Mathematics and Statistics Queen’s University Kingston, Ontario K7L 3N6, email: [email protected]
A. V. Geramita
Affiliation:
Department of Mathematics and Statistics Queen’s University Kingston, Ontario K7L 3N6, email: [email protected]
I. P. Hughes
Affiliation:
Department of Mathematics and Statistics Queen’s University Kingston, Ontario K7L 3N6, email: [email protected]
R. J. Shank
Affiliation:
Department of Mathematics and Statistics Queen’s University Kingston, Ontario K7L 3N6, email: [email protected]
D. L. Wehlau
Affiliation:
Department of Mathematics and Statistics Queen’s University Kingston, Ontario K7L 3N6, email: [email protected] Department of Mathematics and Computer Science RoyalMilitary College Kingston, Ontario K7K 7B4, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper contains two essentially independent results in the invariant theory of finite groups. First we prove that, for any faithful representation of a non-trivial $p$-group over a field of characteristic $p$, the ring of vector invariants of 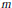$m$ copies of that representation is not Cohen-Macaulay for 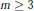$m\,\ge \,3$. In the second section of the paper we use Poincaré series methods to produce upper bounds for the degrees of the generators for the ring of invariants as long as that ring is Gorenstein. We prove that, for a finite non-trivial group 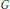$G$ and a faithful representation of dimension $n$ with 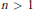$n\,>\,1$, if the ring of invariants is Gorenstein then the ring is generated in degrees less than or equal to 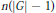$n(\left| G \right|\,-\,1)$. If the ring of invariants is a hypersurface, the upper bound can be improved to 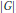$\left| G \right|$.

Keywords

13A50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 155 - 161
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Benson, D. J., Polynomial invariants of finite groups. London Math. Soc. Lecture Note Ser. 190, Cambridge University Press, Cambridge, 1993.Google Scholar
[2] Bruns, W. and Herzog, J., Cohen-Macaulay rings. Cambridge Stud. Adv. Math. 39, Cambridge University Press, Cambridge, 1993.Google Scholar
[3] Eagon, J. A. and Hochster, M., Cohen-Macaulay rings, invariant theory, and the generic perfection of determinantal loci. Amer. J. Math. 93 (1971), 1020–1058.Google Scholar
[4] Noether, E., Der endlichkeitssatz der invarianten endlicher gruppen. Math. Ann. 77 (1916), 89–92.Google Scholar
[5] Smith, L., Polynomial invariants of finite groups. A. K. Peters, Wellesley, MA, 1995.Google Scholar
[6] Smith, L., Polynomial invariants of finite groups—a survey of recent developments. Bull. Amer. Math. Soc. (3) 34 (1997), 211–248.Google Scholar
[7] Springer, T. A., Invariant Theory. Lecture Notes in Math. 585, Springer-Verlag, Berlin, 1977.Google Scholar
[8] Stanley, R. P., Invariants of finite groups and their applications to combinatorics. Bull. Amer. Math. Soc. (3) 1 (1979), 475–511.Google Scholar
[9] Weyl, H., The classical groups. Princeton University Press, Princeton, NJ, 1946.Google Scholar