Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T01:19:28.433Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Finite Dehn Fillings

Published online by Cambridge University Press:  20 November 2018

S. Boyer  and
X. Zhang
S. Boyer
Affiliation:
Département de mathématiques UQAM P.O. Box 8888, Station A Montréal, Québec H3C 3P8, email: [email protected]
X. Zhang
Affiliation:
Department of Mathematics Oklahoma State University Stillwater, Oklahoma 74078-0001 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 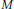$M$ be a compact, connected, orientable 3-manifold whose boundary is a torus and whose interior admits a complete hyperbolic metric of finite volume. In this paper we show that if theminimal Culler-Shalen norm of a non-zero class in 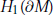${{H}_{1}}(\partial M)$ is larger than 8, then the finite surgery conjecture holds for 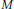$M$. This means that there are at most 5 Dehn fillings of 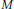$M$ which can yieldmanifolds having cyclic or finite fundamental groups and the distance between any slopes yielding such manifolds is at most 3.

Keywords

57M2557R65
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 149 - 154
Copyright
Copyright © Canadian Mathematical Society 1999

References

[BH] Bleiler, S. and Hodgson, C., Space forms and Dehn fillings. Topology 35 (1996), 809–833.Google Scholar
[BMZ] Boyer, S., Mattman, T. and Zhang, X., The fundamental polygons of twisted knots and the (−2; 3; 7) pretzel knot. Knots ‘96,World Scientific Publishing Co. Pte. Ltd., 1997, 159–172.Google Scholar
[BZ1] Boyer, S. and Zhang, X., Finite Dehn surgery on knots. J. Amer.Math. Soc. 9 (1996), 1005–1050.Google Scholar
[BZ2] Boyer, S. and Zhang, X., On Culler-Shalen seminorms and Dehn filling. Preprint.Google Scholar
[CGLS] Culler, M., Gordon, C., Luecke, J. and Shalen, P., Dehn surgery on knots. Ann. of Math. 125 (1987), 237–300.Google Scholar
[G] Gordon, C., Dehn surgery on knots. Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), 631–642, Math. Soc. Japan, Tokyo, 1991.Google Scholar
[Mi] Milnor, J., Groups which act on Sn without fixed points. Amer. J. Math. 79 (1957), 623–631.Google Scholar
[W] Weeks, J., Ph.D. thesis, Princeton University, 1985.Google Scholar