Published online by Cambridge University Press: 20 November 2018
Let 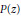 $P\left( z \right)$ be a polynomial of degree not exceeding
$P\left( z \right)$ be a polynomial of degree not exceeding  $n$ and let
$n$ and let 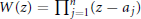 $W\left( z \right)\,=\,\prod\nolimits_{j=1}^{n}{\left( z\,-\,{{a}_{j}} \right)}$ where
$W\left( z \right)\,=\,\prod\nolimits_{j=1}^{n}{\left( z\,-\,{{a}_{j}} \right)}$ where 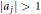 $\left| {{a}_{j}} \right|\,>\,1$,
$\left| {{a}_{j}} \right|\,>\,1$, 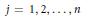 $j\,=\,1,\,2,\,.\,.\,.\,,\,n$. If the rational function
$j\,=\,1,\,2,\,.\,.\,.\,,\,n$. If the rational function 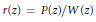 $r\left( z \right)\,=\,{P\left( z \right)}/{W\left( z \right)}\;$ does not vanish in
$r\left( z \right)\,=\,{P\left( z \right)}/{W\left( z \right)}\;$ does not vanish in 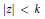 $\left| z \right|\,<\,k$, then for
$\left| z \right|\,<\,k$, then for 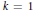 $k\,=\,1$ it is known that
$k\,=\,1$ it is known that
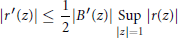 $$\left| {{r}^{'}}\left( z \right) \right|\le \frac{1}{2}\left| {{B}^{'}}(z) \right|_{\left| z \right|=1}^{\text{Sup}}\left| r(z) \right|$$
$$\left| {{r}^{'}}\left( z \right) \right|\le \frac{1}{2}\left| {{B}^{'}}(z) \right|_{\left| z \right|=1}^{\text{Sup}}\left| r(z) \right|$$
where 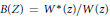 $B\left( Z \right)\,=\,{{{W}^{*}}\left( z \right)}/{W\left( z \right)}\;$ and
$B\left( Z \right)\,=\,{{{W}^{*}}\left( z \right)}/{W\left( z \right)}\;$ and  ${{W}^{*}}\left( z \right)\,=\,{{z}^{n}}\overline{W\left( {1}/{\overline{z}}\; \right)}$. In the paper we consider the case when
${{W}^{*}}\left( z \right)\,=\,{{z}^{n}}\overline{W\left( {1}/{\overline{z}}\; \right)}$. In the paper we consider the case when  $k\,>\,1$ and obtain a sharp result. We also show that
$k\,>\,1$ and obtain a sharp result. We also show that
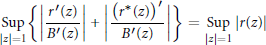 $$\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left\{ \left| \frac{{{r}^{\prime }}\left( z \right)}{{{B}^{\prime }}\left( z \right)} \right|+\left| \frac{{{\left( {{r}^{*}}\left( z \right) \right)}^{\prime }}}{{{B}^{\prime }}\left( z \right)} \right| \right\}=\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left| r\left( z \right) \right|$$
$$\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left\{ \left| \frac{{{r}^{\prime }}\left( z \right)}{{{B}^{\prime }}\left( z \right)} \right|+\left| \frac{{{\left( {{r}^{*}}\left( z \right) \right)}^{\prime }}}{{{B}^{\prime }}\left( z \right)} \right| \right\}=\underset{\left| z \right|=1}{\mathop{\text{Sup}}}\,\left| r\left( z \right) \right|$$
where 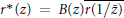 ${{r}^{*}}\left( z \right)\,=\,B\left( z \right)\overline{r\left( {1}/{\overline{z}}\; \right)}$, and as a consquence of this result, we present a generalization of a theorem of O’Hara and Rodriguez for self-inversive polynomials. Finally, we establish a similar result when supremum is replaced by infimum for a rational function which has all its zeros in the unit circle.
${{r}^{*}}\left( z \right)\,=\,B\left( z \right)\overline{r\left( {1}/{\overline{z}}\; \right)}$, and as a consquence of this result, we present a generalization of a theorem of O’Hara and Rodriguez for self-inversive polynomials. Finally, we establish a similar result when supremum is replaced by infimum for a rational function which has all its zeros in the unit circle.