15 results
On tau-tilting subcategories
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-38
-
- Article
-
- You have access
- HTML
- Export citation
Three Schur functors related to pre-Lie algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 441-458
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
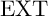 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Pirashvili-type theorem for functors on non-empty finite sets
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1-61
- Print publication:
- January 2023
-
- Article
- Export citation
THE YONEDA EXT AND ARBITRARY COPRODUCTS IN ABELIAN CATEGORIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 277-291
- Print publication:
- May 2022
-
- Article
- Export citation
HOMOLOGY THEORIES FOR COMPLEXES BASED ON FLATS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 02 December 2019, pp. 27-44
- Print publication:
- January 2021
-
- Article
- Export citation
Décomposition de Hodge pour l’homologie stable des groupes d’automorphismes des groupes libres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1794-1844
- Print publication:
- September 2019
-
- Article
- Export citation
DIFFERENTIAL GRADED ENDOMORPHISM ALGEBRAS, COHOMOLOGY RINGS AND DERIVED EQUIVALENCES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 557-573
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Tilting subcategories with respect to cotorsion triples in abelian categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 703-726
- Print publication:
- August 2017
-
- Article
- Export citation
WEAK INJECTIVE AND WEAK FLAT COMPLEXES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 539-557
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Spaces with Noetherian cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 13-25
-
- Article
-
- You have access
- Export citation
A Künneth Theorem for p-Adic Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 3 / 01 September 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 440-446
- Print publication:
- 01 September 2007
-
- Article
-
- You have access
- Export citation
Finite Generation of the Extension Algebra Ext
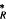 (M, M)
(M, M)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-374
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
The Splitting of the Hochschild-Serre Spectral Sequence for a Product of Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 2 / 01 June 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 181-183
- Print publication:
- 01 June 1990
-
- Article
-
- You have access
- Export citation
On the Criteria of D.D. Anderson for Invertible and Flat Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 1 / 01 March 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 25-32
- Print publication:
- 01 March 1986
-
- Article
-
- You have access
- Export citation

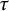
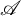
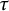
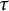
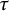
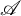
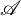
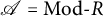
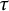
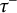
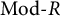
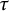
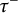
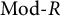
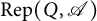
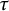
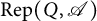
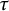
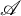
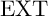
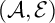
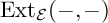





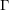
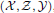 , the notion of
, the notion of 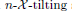 subcategories in an abelian category
subcategories in an abelian category 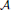 is introduced. It is proved that a virtually Gorenstein ring
is introduced. It is proved that a virtually Gorenstein ring 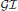 of Gorenstein injective
of Gorenstein injective 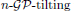 with respect to the cotorsion triple
with respect to the cotorsion triple 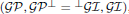 , where
, where 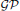 stands for the subcategory of Gorenstein projectives. In the case when a subcategory
stands for the subcategory of Gorenstein projectives. In the case when a subcategory 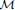 of
of 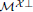 admits a right
admits a right 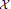 -coresolving covariantly finite and closed under direct summands.
-coresolving covariantly finite and closed under direct summands.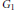
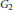
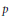
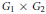
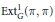
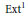
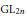
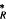 (M, M)
(M, M)
