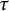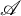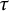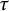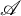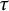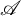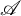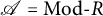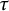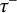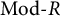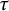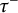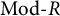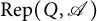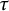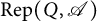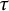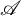1 Introduction
Tilting theory is one of the most prominent tools in the representation theory of Artin algebras. The classical tilting modules were introduced by Brenner and Butler [Reference Brenner and Butler15], and Happel and Ringel [Reference Happel and Ringel23] as an axiomatization of the reflection functors of Bernstein, Gelfand, and Ponomarev [Reference Bernstein, Gelfand and Ponomarev12] and Auslander, Platzek, and Reiten [Reference Auslander, Platzeck and Reiten5]. It has been shown by Bongartz [Reference Bongartz13] that every partial tilting module can be completed to a tilting module and by Happel and Unger [Reference Happel and Unger24] that every almost complete tilting module can be completed in at most two ways. However, there are examples of almost complete tilting modules that have exactly one complement.
Several years later, and inspired by the cluster algebras defined by Fomin and Zelevnisky in [Reference Fomin and Zelevinsky22], Adachi, Iyama, and Reiten introduced
![]() $\tau $
-tilting theory [Reference Adachi, Iyama and Reiten1]. This is a generalization of classical tilting theory in which every almost complete support
$\tau $
-tilting theory [Reference Adachi, Iyama and Reiten1]. This is a generalization of classical tilting theory in which every almost complete support
![]() $\tau $
-tilting module has exactly two complements, allowing to introduce a notion of mutation among these objects. The success of
$\tau $
-tilting module has exactly two complements, allowing to introduce a notion of mutation among these objects. The success of
![]() $\tau $
-tilting theory was immediate, explaining several phenomena in the module category of Artin algebras, as well as new connections between representation theory and other areas of mathematics (see [Reference Treffinger33]).
$\tau $
-tilting theory was immediate, explaining several phenomena in the module category of Artin algebras, as well as new connections between representation theory and other areas of mathematics (see [Reference Treffinger33]).
Due to the effectiveness of
![]() $\tau $
-tilting theory for the study of the categories of finitely presented modules, many mathematicians have introduced theories generalizing
$\tau $
-tilting theory for the study of the categories of finitely presented modules, many mathematicians have introduced theories generalizing
![]() $\tau $
-tilting theory, and its dual, to other contexts. For instance, there are the works of Angeleri Hügel, Marks, and Vitoria [Reference Angeleri Hügel, Marks and Vitória2] and Breaz and Pop [Reference Breaz and Pop14] for the module category of rings; Iyama, Jørgensen, and Yang [Reference Iyama, Jørgensen and Yang26] for functor categories; or Liu and Zhou for Hom-finite abelian categories with enough projective objects [Reference Liu and Zhou28].
$\tau $
-tilting theory, and its dual, to other contexts. For instance, there are the works of Angeleri Hügel, Marks, and Vitoria [Reference Angeleri Hügel, Marks and Vitória2] and Breaz and Pop [Reference Breaz and Pop14] for the module category of rings; Iyama, Jørgensen, and Yang [Reference Iyama, Jørgensen and Yang26] for functor categories; or Liu and Zhou for Hom-finite abelian categories with enough projective objects [Reference Liu and Zhou28].
In this paper, we are interested in studying
![]() $\tau $
-tilting theory in arbitrary abelian categories with enough projective objects. Since there is no notion of Auslander–Reiten translation
$\tau $
-tilting theory in arbitrary abelian categories with enough projective objects. Since there is no notion of Auslander–Reiten translation
![]() $\tau $
in such general categories, the definition of support
$\tau $
in such general categories, the definition of support
![]() $\tau $
-tilting subcategories needs to be made with no mention of it. We follow [Reference Iyama, Jørgensen and Yang26, Reference Liu and Zhou28] to define support
$\tau $
-tilting subcategories needs to be made with no mention of it. We follow [Reference Iyama, Jørgensen and Yang26, Reference Liu and Zhou28] to define support
![]() $\tau $
-tilting subcategories.
$\tau $
-tilting subcategories.
Definition 1.1 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {T}$
be an additive contravariantly finite full subcategory of
$\mathscr {T}$
be an additive contravariantly finite full subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {T}$
is called a support
$\mathscr {T}$
is called a support
![]() $\tau $
-tilting subcategory if:
$\tau $
-tilting subcategory if:
-
1.
 ${\mathrm {Ext}}^1_{\mathscr {A}}(T_1,{\mathrm {Fac}}(T_2))=0,$
for all
${\mathrm {Ext}}^1_{\mathscr {A}}(T_1,{\mathrm {Fac}}(T_2))=0,$
for all
 $T_1, T_2 \in \mathscr {T}$
.
$T_1, T_2 \in \mathscr {T}$
. -
2. For any projective P in
 $\mathscr {A}$
, there exists an exact sequence such that
$\mathscr {A}$
, there exists an exact sequence such that $$\begin{align*}P \stackrel{f}{\longrightarrow} T^0 \longrightarrow T^1 \longrightarrow 0 \end{align*}$$
$$\begin{align*}P \stackrel{f}{\longrightarrow} T^0 \longrightarrow T^1 \longrightarrow 0 \end{align*}$$
 $T^0$
and
$T^0$
and
 $T^1$
are in
$T^1$
are in
 $\mathscr {T}$
and f is a left
$\mathscr {T}$
and f is a left
 $\mathscr {T}$
-approximation of P.
$\mathscr {T}$
-approximation of P.
By
![]() ${\mathrm {Fac}}(T)$
, for an object
${\mathrm {Fac}}(T)$
, for an object
![]() $T \in \mathscr {A}$
, we mean the full subcategory consisting of factor objects of finite direct sums of copies of T.
$T \in \mathscr {A}$
, we mean the full subcategory consisting of factor objects of finite direct sums of copies of T.
The idea of generalizing a well-behaved theory from the category of finitely presented modules of an Artin algebra to more general abelian categories is not exclusive to
![]() $\tau $
-tilting theory. Indeed, Beligiannis introduced tilting theory for arbitrary abelian categories in [Reference Beligiannis10] at the beginning of the millennium (see also [Reference Beligiannis and Reiten11]). In recent years, the work of Bauer, Botnan, Oppermann, and Steen [Reference Bauer, Botnan, Oppermann and Steen7] has found a striking application of this theory of Beligiannis in persistence theory and topological data analysis (TDA). One of the main results in [Reference Bauer, Botnan, Oppermann and Steen7] is a bijection between tilting subcategories of an abelian category with enough projective objects and the collection of cotorsion torsion triples in the same category. The motivation that started this collaboration is to find a version of [Reference Bauer, Botnan, Oppermann and Steen7, Theorem 2.29] for support
$\tau $
-tilting theory. Indeed, Beligiannis introduced tilting theory for arbitrary abelian categories in [Reference Beligiannis10] at the beginning of the millennium (see also [Reference Beligiannis and Reiten11]). In recent years, the work of Bauer, Botnan, Oppermann, and Steen [Reference Bauer, Botnan, Oppermann and Steen7] has found a striking application of this theory of Beligiannis in persistence theory and topological data analysis (TDA). One of the main results in [Reference Bauer, Botnan, Oppermann and Steen7] is a bijection between tilting subcategories of an abelian category with enough projective objects and the collection of cotorsion torsion triples in the same category. The motivation that started this collaboration is to find a version of [Reference Bauer, Botnan, Oppermann and Steen7, Theorem 2.29] for support
![]() $\tau $
-tilting subcategories. To do that, we first need an adequate notion of triple. Inspired by [Reference Beligiannis and Reiten11, Lemma V.3.3], we define
$\tau $
-tilting subcategories. To do that, we first need an adequate notion of triple. Inspired by [Reference Beligiannis and Reiten11, Lemma V.3.3], we define
![]() $\tau $
-cotorsion torsion triple as follows.
$\tau $
-cotorsion torsion triple as follows.
Definition 1.2 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. A triple of full subcategories
$\mathscr {A}$
be an abelian category with enough projective objects. A triple of full subcategories
![]() $(\mathscr {C}, \mathscr {D}, \mathscr {F})$
of
$(\mathscr {C}, \mathscr {D}, \mathscr {F})$
of
![]() $\mathscr {A}$
is called a
$\mathscr {A}$
is called a
![]() $\tau $
-cotorsion torsion triple if:
$\tau $
-cotorsion torsion triple if:
-
1.
 $\mathscr {C} = {}^{\perp _1}\mathscr {D}$
.
$\mathscr {C} = {}^{\perp _1}\mathscr {D}$
. -
2. For every projective object
 $P \in \mathscr {A}$
, there exists an exact sequence where
$P \in \mathscr {A}$
, there exists an exact sequence where $$\begin{align*}P \stackrel{f}\longrightarrow {D}\longrightarrow C \longrightarrow 0, \end{align*}$$
$$\begin{align*}P \stackrel{f}\longrightarrow {D}\longrightarrow C \longrightarrow 0, \end{align*}$$
 $D \in \mathscr {C}\cap \mathscr {D}$
,
$D \in \mathscr {C}\cap \mathscr {D}$
,
 $C \in \mathscr {C}$
, and f is a left
$C \in \mathscr {C}$
, and f is a left
 $\mathscr {D}$
-approximation.
$\mathscr {D}$
-approximation.
-
3.
 $\mathscr {C}\cap \mathscr {D}$
is a contravariantly finite subcategory of
$\mathscr {C}\cap \mathscr {D}$
is a contravariantly finite subcategory of
 $\mathscr {A}$
.
$\mathscr {A}$
. -
4.
 $(\mathscr {D}, \mathscr {F})$
is a torsion pair in
$(\mathscr {D}, \mathscr {F})$
is a torsion pair in
 $\mathscr {A}$
.
$\mathscr {A}$
.
Having the notion of
![]() $\tau $
-cotorsion torsion triple, we can show the desired bijection in an abelian category with enough projective objects.
$\tau $
-cotorsion torsion triple, we can show the desired bijection in an abelian category with enough projective objects.
Theorem 1.3 (Theorem 5.7)
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Then there are bijections
$\mathscr {A}$
be an abelian category with enough projective objects. Then there are bijections
 $$ \begin{align*} \Phi: \{\mbox{support } \tau\mbox{-tilting subcategories}\}& \longrightarrow \{ \tau\mbox{-cotorsion torsion triples}\}\\ \mathscr{T}& \longmapsto ({}^{\perp_1}{(\mathrm{Fac}(\mathscr{T}))}, \mathrm{Fac}(\mathscr{T}), \mathscr{T}^{\perp_0}),\\[5pt] \Psi: \{ \tau\mbox{-cotorsion torsion triples}\} & \longrightarrow \{\mbox{support } \tau\mbox{-tilting subcategories}\}\\ (\mathscr{C}, \mathscr{D}, \mathscr{F}) & \longmapsto \mathscr{C}\cap\mathscr{D} \end{align*} $$
$$ \begin{align*} \Phi: \{\mbox{support } \tau\mbox{-tilting subcategories}\}& \longrightarrow \{ \tau\mbox{-cotorsion torsion triples}\}\\ \mathscr{T}& \longmapsto ({}^{\perp_1}{(\mathrm{Fac}(\mathscr{T}))}, \mathrm{Fac}(\mathscr{T}), \mathscr{T}^{\perp_0}),\\[5pt] \Psi: \{ \tau\mbox{-cotorsion torsion triples}\} & \longrightarrow \{\mbox{support } \tau\mbox{-tilting subcategories}\}\\ (\mathscr{C}, \mathscr{D}, \mathscr{F}) & \longmapsto \mathscr{C}\cap\mathscr{D} \end{align*} $$
which are mutually inverse. Moreover, these bijections restrict to bijections between the collection of tilting subcategories of
![]() $\mathscr {A}$
and the collection of cotorsion torsion triples in
$\mathscr {A}$
and the collection of cotorsion torsion triples in
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
We note that Buan and Zhou [Reference Buan and Zhou16] introduced the notion of left weak cotorsion torsion triple to provide a version of [Reference Bauer, Botnan, Oppermann and Steen7, Theorem 2.29] for support
![]() $\tau $
-tilting modules in
$\tau $
-tilting modules in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
, where
${\mathrm {{mod\mbox {-}}}}\Lambda $
, where
![]() $\Lambda $
is an Artin algebra. In Theorem 4.10, we show that a triple
$\Lambda $
is an Artin algebra. In Theorem 4.10, we show that a triple
![]() $(\mathscr {C}, \mathscr {D}, \mathscr {F})$
of subcategories of
$(\mathscr {C}, \mathscr {D}, \mathscr {F})$
of subcategories of
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
is a left weak cotorsion torsion triple if and only if it is a
${\mathrm {{mod\mbox {-}}}}\Lambda $
is a left weak cotorsion torsion triple if and only if it is a
![]() $\tau $
-cotorsion torsion triple.
$\tau $
-cotorsion torsion triple.
One of the main properties of support
![]() $\tau $
-tilting modules is that they generate functorially finite torsion classes in module categories. As a consequence of our results, we obtain the following corollary (see Theorem 5.7 and Corollary 4.8).
$\tau $
-tilting modules is that they generate functorially finite torsion classes in module categories. As a consequence of our results, we obtain the following corollary (see Theorem 5.7 and Corollary 4.8).
Corollary 1.4 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects, and let
$\mathscr {A}$
be an abelian category with enough projective objects, and let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() ${\mathrm {Fac}}(\mathscr {T})$
is a functorially finite torsion class in
${\mathrm {Fac}}(\mathscr {T})$
is a functorially finite torsion class in
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
For
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
, using results of [Reference Adachi, Iyama and Reiten1], it is shown that a module T in
${\mathrm {{mod\mbox {-}}}}\Lambda $
, using results of [Reference Adachi, Iyama and Reiten1], it is shown that a module T in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
is a support
${\mathrm {{mod\mbox {-}}}}\Lambda $
is a support
![]() $\tau $
-tilting module if and only if
$\tau $
-tilting module if and only if
![]() ${\mathrm {add}}(T)$
is a support
${\mathrm {add}}(T)$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
. On the other hand, T is a support
${\mathrm {{mod\mbox {-}}}} \Lambda $
. On the other hand, T is a support
![]() $\tau ^-$
-tilting module if and only if
$\tau ^-$
-tilting module if and only if
![]() ${\mathrm {add}}(T)$
is a support
${\mathrm {add}}(T)$
is a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
(see Propositions 5.9 and 6.11).
${\mathrm {{mod\mbox {-}}}} \Lambda $
(see Propositions 5.9 and 6.11).
A prominent example of an abelian category with enough projective objects is
![]() $\mathrm{Mod}\mbox {-}R$
, the category of modules over a unitary associative ring R. Angeleri Hügel, Marks, and Vitoria [Reference Angeleri Hügel, Marks and Vitória2] introduced the concept of silting modules in
$\mathrm{Mod}\mbox {-}R$
, the category of modules over a unitary associative ring R. Angeleri Hügel, Marks, and Vitoria [Reference Angeleri Hügel, Marks and Vitória2] introduced the concept of silting modules in
![]() $\mathrm{Mod}\mbox {-}R$
, as a generalization of support
$\mathrm{Mod}\mbox {-}R$
, as a generalization of support
![]() $\tau $
-tilting modules. They showed that if R is an Artin algebra, finitely presented silting modules coincide with the support
$\tau $
-tilting modules. They showed that if R is an Artin algebra, finitely presented silting modules coincide with the support
![]() $\tau $
-tilting modules of [Reference Adachi, Iyama and Reiten1]. As the categorical dual of silting modules, Breaz and Pop [Reference Breaz and Pop14] introduced the notion of cosilting modules in
$\tau $
-tilting modules of [Reference Adachi, Iyama and Reiten1]. As the categorical dual of silting modules, Breaz and Pop [Reference Breaz and Pop14] introduced the notion of cosilting modules in
![]() $\mathrm{Mod}\mbox {-}R$
and showed that over Artin algebras finitely copresented cosilting modules coincide with the support
$\mathrm{Mod}\mbox {-}R$
and showed that over Artin algebras finitely copresented cosilting modules coincide with the support
![]() $\tau ^-$
-tilting modules.
$\tau ^-$
-tilting modules.
We study the connection between silting (resp. cosilting) modules in
![]() $\mathrm{Mod}\mbox {-}R$
with the
$\mathrm{Mod}\mbox {-}R$
with the
![]() $\tau $
-tilting (resp.
$\tau $
-tilting (resp.
![]() $\tau ^-$
-tilting) subcategories of
$\tau ^-$
-tilting) subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
. Furthermore, we characterize all support
$\mathrm{Mod}\mbox {-}R$
. Furthermore, we characterize all support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
. In particular, we provide a bijection between the equivalence classes of all support
$\mathrm{Mod}\mbox {-}R$
. In particular, we provide a bijection between the equivalence classes of all support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
and the collection of all equivalence classes of certain R-modules, the so-called finendo quasitilting R-modules (see Theorem 7.1.10). It is known that all silting modules are finendo quasitilting. Dually, we also characterize all support
$\mathrm{Mod}\mbox {-}R$
and the collection of all equivalence classes of certain R-modules, the so-called finendo quasitilting R-modules (see Theorem 7.1.10). It is known that all silting modules are finendo quasitilting. Dually, we also characterize all support
![]() $\tau ^{-}$
-tilting subcategories of
$\tau ^{-}$
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
by providing a bijection between the equivalence classes of all support
$\mathrm{Mod}\mbox {-}R$
by providing a bijection between the equivalence classes of all support
![]() $\tau ^-$
-tilting subcategories of
$\tau ^-$
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
and the collection of all equivalent classes of the quasicotilting R-modules.
$\mathrm{Mod}\mbox {-}R$
and the collection of all equivalent classes of the quasicotilting R-modules.
Toward the end of the paper, we provide applications of this theory to the category of the representations of a finite and acyclic quiver in an abelian category
![]() $\mathscr {A}$
with enough projective objects. Let Q be such a quiver. It is known that the category
$\mathscr {A}$
with enough projective objects. Let Q be such a quiver. It is known that the category
![]() $\mathrm {Rep}(Q, \mathscr {A})$
of representations of Q over
$\mathrm {Rep}(Q, \mathscr {A})$
of representations of Q over
![]() $\mathscr {A}$
is again an abelian category with enough projective objects. See Section 8 for more details. We give a recipe to construct support
$\mathscr {A}$
is again an abelian category with enough projective objects. See Section 8 for more details. We give a recipe to construct support
![]() $\tau $
-tilting subcategories in
$\tau $
-tilting subcategories in
![]() $\mathrm {Rep}(Q, \mathscr {A})$
from certain support
$\mathrm {Rep}(Q, \mathscr {A})$
from certain support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathscr {A}$
. More explicitly, we have the following result.
$\mathscr {A}$
. More explicitly, we have the following result.
Theorem 1.5 (Theorem 8.2.2)
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects, and let Q be a finite acyclic quiver. Let
$\mathscr {A}$
be an abelian category with enough projective objects, and let Q be a finite acyclic quiver. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
such that the induced torsion pair
$\mathscr {A}$
such that the induced torsion pair
![]() $({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is hereditary. Then
$({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is hereditary. Then
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm {Rep}(Q, \mathscr {A})$
.
$\mathrm {Rep}(Q, \mathscr {A})$
.
Note that
is the right adjoint of the evaluation functor
![]() $e_i: \mathrm {Rep}(Q, \mathscr {A})\longrightarrow \mathscr {A}$
(see Section 8.1 for more details).
$e_i: \mathrm {Rep}(Q, \mathscr {A})\longrightarrow \mathscr {A}$
(see Section 8.1 for more details).
Let
![]() ${\mathrm {Prj}}(\mathscr {A})$
denote the category of all projective objects in
${\mathrm {Prj}}(\mathscr {A})$
denote the category of all projective objects in
![]() $\mathscr {A}$
. In [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9], the authors have shown that
$\mathscr {A}$
. In [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9], the authors have shown that
is a tilting subcategory of
![]() $\mathscr {A}$
. Then the previous result can be seen as a generalization of this result since
$\mathscr {A}$
. Then the previous result can be seen as a generalization of this result since
![]() $\mathscr {A} = {\mathrm {Fac}}({\mathrm {Prj}}(\mathscr {A}))$
is closed under kernels of epimorphisms.
$\mathscr {A} = {\mathrm {Fac}}({\mathrm {Prj}}(\mathscr {A}))$
is closed under kernels of epimorphisms.
Throughout the paper, several examples are provided using the theory of persistent modules, which are central objects of study in TDA. We refer the reader to the survey [Reference Carlsson17] by Carlsson, or the book [Reference Oudot29] by Oudot, for an introduction to TDA and connections to quiver representations.
The paper is structured as follows. In Section 2, we fix the notations and give the necessary background for the rest of the paper. In Section 3, we define support
![]() $\tau $
-tilting subcategories in abelian categories with enough projective objects and we give some of its basic properties. Then, in Section 4, we introduce and study the notion of
$\tau $
-tilting subcategories in abelian categories with enough projective objects and we give some of its basic properties. Then, in Section 4, we introduce and study the notion of
![]() $\tau $
-cotorsion torsion triples. We also compare
$\tau $
-cotorsion torsion triples. We also compare
![]() $\tau $
-cotorsion torsion triples with the left weak cotorsion torsion triples of [Reference Buan and Zhou16]. In Section 5, we show the bijection between support
$\tau $
-cotorsion torsion triples with the left weak cotorsion torsion triples of [Reference Buan and Zhou16]. In Section 5, we show the bijection between support
![]() $\tau $
-tilting subcategories and
$\tau $
-tilting subcategories and
![]() $\tau $
-cotorsion torsion triples. Section 6 is a compilation of dual definitions and results. In Section 7, we study support
$\tau $
-cotorsion torsion triples. Section 6 is a compilation of dual definitions and results. In Section 7, we study support
![]() $\tau $
- and
$\tau $
- and
![]() $\tau ^-$
- tilting subcategories in
$\tau ^-$
- tilting subcategories in
![]() $\mathrm{Mod}\mbox {-}R$
, where R is a unitary associative ring, and show how they are connected to the silting and cosilting theory. We end the paper in Section 8 where we study support
$\mathrm{Mod}\mbox {-}R$
, where R is a unitary associative ring, and show how they are connected to the silting and cosilting theory. We end the paper in Section 8 where we study support
![]() $\tau $
-tilting subcategories and (co)silting objects in the category
$\tau $
-tilting subcategories and (co)silting objects in the category
![]() $\mathrm {Rep}(Q, \mathscr {A})$
of quiver representations over
$\mathrm {Rep}(Q, \mathscr {A})$
of quiver representations over
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
2 Preliminaries
Let
![]() $\mathscr {A}$
be an abelian category. In this paper, by subcategory, we always mean a full subcategory. Let
$\mathscr {A}$
be an abelian category. In this paper, by subcategory, we always mean a full subcategory. Let
![]() $\mathscr {X}$
be a subcategory of
$\mathscr {X}$
be a subcategory of
![]() $\mathscr {A}$
. A morphism
$\mathscr {A}$
. A morphism
![]() $\varphi : X \longrightarrow A$
, where A is an object of
$\varphi : X \longrightarrow A$
, where A is an object of
![]() $\mathscr {A}$
, is called a right
$\mathscr {A}$
, is called a right
![]() $\mathscr {X}$
-approximation of A if,
$\mathscr {X}$
-approximation of A if,
![]() $X \in \mathscr {X}$
and for every
$X \in \mathscr {X}$
and for every
![]() $X' \in \mathscr {X}$
, the induced morphism
$X' \in \mathscr {X}$
, the induced morphism
![]() $\mathscr {A}(X', X) \longrightarrow \mathscr {A}(X', A) \longrightarrow 0$
of abelian groups is exact. We say that
$\mathscr {A}(X', X) \longrightarrow \mathscr {A}(X', A) \longrightarrow 0$
of abelian groups is exact. We say that
![]() $\mathscr {X}$
is a contravariantly finite subcategory of
$\mathscr {X}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
if every object A of
$\mathscr {A}$
if every object A of
![]() $\mathscr {A}$
admits a right
$\mathscr {A}$
admits a right
![]() $\mathscr {X}$
-approximation. The notions of left
$\mathscr {X}$
-approximation. The notions of left
![]() $\mathscr {X}$
-approximations and covariantly finite subcategories are defined dually. Moreover, we say that
$\mathscr {X}$
-approximations and covariantly finite subcategories are defined dually. Moreover, we say that
![]() $\mathscr {X}$
is a functorially finite subcategory of
$\mathscr {X}$
is a functorially finite subcategory of
![]() $\mathscr {A}$
if it is both a contravariantly finite and a covariantly finite subcategory of
$\mathscr {A}$
if it is both a contravariantly finite and a covariantly finite subcategory of
![]() $\mathscr {A}$
. If
$\mathscr {A}$
. If
![]() $\mathscr {X}$
is closed under taking finite direct sums and direct summands, we say that it is additively closed.
$\mathscr {X}$
is closed under taking finite direct sums and direct summands, we say that it is additively closed.
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. For a nonnegative integer n, we set
$\mathscr {A}$
be an abelian category with enough projective objects. For a nonnegative integer n, we set
Note that
![]() ${\mathrm {Ext}}^0$
is just the usual Hom-functor.
${\mathrm {Ext}}^0$
is just the usual Hom-functor.
2.1 (Pointwise finite-dimensional representations)
Let k be a field, and let
![]() $(\mathcal {X} , \leq )$
be a poset. Consider
$(\mathcal {X} , \leq )$
be a poset. Consider
![]() $\mathcal {X} $
as a category. A persistence module is a (covariant and additive) functor
$\mathcal {X} $
as a category. A persistence module is a (covariant and additive) functor
![]() $V: \mathcal {X} \to \mathrm{Mod}\mbox {-}k$
from
$V: \mathcal {X} \to \mathrm{Mod}\mbox {-}k$
from
![]() $\mathcal {X} $
to
$\mathcal {X} $
to
![]() $\mathrm{Mod}\mbox {-}k$
, the category of k-vector spaces. A persistence module V is called a pointwise finite-dimensional representation of
$\mathrm{Mod}\mbox {-}k$
, the category of k-vector spaces. A persistence module V is called a pointwise finite-dimensional representation of
![]() $\mathcal {X} $
if it is a functor from
$\mathcal {X} $
if it is a functor from
![]() $\mathcal {X} $
to
$\mathcal {X} $
to
![]() ${\mathrm {{mod\mbox {-}}}} k$
, the category of finite-dimensional vector spaces.
${\mathrm {{mod\mbox {-}}}} k$
, the category of finite-dimensional vector spaces.
The abelian category of pointwise finite-dimensional representations will be denoted by
![]() $\mathrm { Rep}_k^{\mathrm {pfd}}\mathcal {X} $
. A subset
$\mathrm { Rep}_k^{\mathrm {pfd}}\mathcal {X} $
. A subset
![]() $\mathcal {C} $
of
$\mathcal {C} $
of
![]() $\mathcal {X} $
is called a convex subset if for every
$\mathcal {X} $
is called a convex subset if for every
![]() $x \leq y\in \mathcal {C} $
,
$x \leq y\in \mathcal {C} $
,
![]() $x\leq z\leq y$
implies
$x\leq z\leq y$
implies
![]() $z\in \mathcal {C} $
. Let
$z\in \mathcal {C} $
. Let
![]() $\mathcal {C} $
be a convex subset of
$\mathcal {C} $
be a convex subset of
![]() $\mathcal {X} $
. The constant representation
$\mathcal {X} $
. The constant representation
![]() $k_{\mathcal {C}} $
is defined by
$k_{\mathcal {C}} $
is defined by
![]() $k_{\mathcal {C}} (x)=k$
, for
$k_{\mathcal {C}} (x)=k$
, for
![]() $x\in \mathcal {C} $
,
$x\in \mathcal {C} $
,
![]() $k_{\mathcal {C}} (x)=0$
, for
$k_{\mathcal {C}} (x)=0$
, for
![]() $x\not \in \mathcal {C} $
and
$x\not \in \mathcal {C} $
and
![]() $k_{\mathcal {C}} (x\leq y)=\mathrm {id}_k$
, for
$k_{\mathcal {C}} (x\leq y)=\mathrm {id}_k$
, for
![]() $x\leq y$
in
$x\leq y$
in
![]() $\mathcal {C} $
. Set
$\mathcal {C} $
. Set
![]() $P_x=k_{\lbrace y\in \mathcal {X} \vert \ y\geq x\rbrace }.$
As an application of Yoneda’s lemma, one can see that, for every
$P_x=k_{\lbrace y\in \mathcal {X} \vert \ y\geq x\rbrace }.$
As an application of Yoneda’s lemma, one can see that, for every
![]() $x \in \mathcal {X} $
,
$x \in \mathcal {X} $
,
![]() $P_x$
is a projective object of
$P_x$
is a projective object of
![]() $\mathrm {Rep}_k^{\mathrm {pfd}}\mathcal {X} $
and, vice versa, all projective modules are of this form (see, e.g., [Reference Bauer, Botnan, Oppermann and Steen7, Section 2]). A representation
$\mathrm {Rep}_k^{\mathrm {pfd}}\mathcal {X} $
and, vice versa, all projective modules are of this form (see, e.g., [Reference Bauer, Botnan, Oppermann and Steen7, Section 2]). A representation
![]() $V\in \mathrm {Rep}_k^{\mathrm {pfd}} \mathcal {X} $
is called finitely generated if there exists an epimorphism of functors
$V\in \mathrm {Rep}_k^{\mathrm {pfd}} \mathcal {X} $
is called finitely generated if there exists an epimorphism of functors
![]() $\bigoplus _{i\in J} P_{x_i}\longrightarrow V$
, where J is a finite indexing set. Moreover, if the kernel of this epimorphism is again finitely generated, it is called finitely presented. We denote the full subcategory of
$\bigoplus _{i\in J} P_{x_i}\longrightarrow V$
, where J is a finite indexing set. Moreover, if the kernel of this epimorphism is again finitely generated, it is called finitely presented. We denote the full subcategory of
![]() $\mathrm {Rep}_k^{\mathrm {pfd}} \mathcal {X} $
consisting of finitely presented representations by
$\mathrm {Rep}_k^{\mathrm {pfd}} \mathcal {X} $
consisting of finitely presented representations by
![]() $\mathrm {Rep}_k^{\mathrm {fp}}\mathcal {X} $
.
$\mathrm {Rep}_k^{\mathrm {fp}}\mathcal {X} $
.
One of the most important cases is when we consider the poset of nonnegative real numbers, denoted by
![]() $\mathbb {R}_{\geq 0}.$
It is proved in [Reference Crawley-Boevey18, Theorem 1.1] that the indecomposable objects in
$\mathbb {R}_{\geq 0}.$
It is proved in [Reference Crawley-Boevey18, Theorem 1.1] that the indecomposable objects in
![]() $\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
are classified by the constant representations
$\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
are classified by the constant representations
![]() $k_{ [x, y)}$
, where
$k_{ [x, y)}$
, where
![]() $x< y\leq \infty $
. Moreover, for each
$x< y\leq \infty $
. Moreover, for each
![]() $x\geq 0$
, the constant representations
$x\geq 0$
, the constant representations
![]() $k_{[ x, \infty )}$
and
$k_{[ x, \infty )}$
and
![]() $k_{[ 0, x)}$
are projective and injective objects, respectively.
$k_{[ 0, x)}$
are projective and injective objects, respectively.
2.2 (Cotorsion torsion triple)
Here, we recall the notion of torsion pairs, cotorsion pairs, and cotorsion torsion triples. Let us begin by the following classical definition of Dickson [Reference Dickson19].
Definition 2.3 Let
![]() $\mathscr {A}$
be an abelian category. A pair
$\mathscr {A}$
be an abelian category. A pair
![]() $(\mathscr {T},\mathscr {F})$
of full subcategories of
$(\mathscr {T},\mathscr {F})$
of full subcategories of
![]() $\mathscr {A}$
is called a torsion pair if
$\mathscr {A}$
is called a torsion pair if
![]() ${\mathrm {Hom}}_{\mathscr {A}}(\mathscr {T},\mathscr {F})=0$
and for every
${\mathrm {Hom}}_{\mathscr {A}}(\mathscr {T},\mathscr {F})=0$
and for every
![]() $A \in \mathscr {A}$
there is a short exact sequence
$A \in \mathscr {A}$
there is a short exact sequence
such that
![]() $tA \in \mathscr {T}$
and
$tA \in \mathscr {T}$
and
![]() $fA \in \mathscr {F}$
.
$fA \in \mathscr {F}$
.
In this case,
![]() $\mathscr {T}$
is called the torsion class and
$\mathscr {T}$
is called the torsion class and
![]() $\mathscr {F}$
is called the torsion-free class. A torsion pair
$\mathscr {F}$
is called the torsion-free class. A torsion pair
![]() $(\mathscr {T}, \mathscr {F})$
is called hereditary if
$(\mathscr {T}, \mathscr {F})$
is called hereditary if
![]() $\mathscr {T}$
is closed under subobjects. It is known that
$\mathscr {T}$
is closed under subobjects. It is known that
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
![]() $\mathscr {F}$
determine each other and the short exact sequence is functorial. See, for instance, [Reference Beligiannis and Reiten11, Section I.1].
$\mathscr {F}$
determine each other and the short exact sequence is functorial. See, for instance, [Reference Beligiannis and Reiten11, Section I.1].
Let
![]() $\mathscr {A} = {\mathrm {{mod\mbox {-}}}} \Lambda $
. By [Reference Smalø32, Theorem 1], if
$\mathscr {A} = {\mathrm {{mod\mbox {-}}}} \Lambda $
. By [Reference Smalø32, Theorem 1], if
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair in
$(\mathscr {T}, \mathscr {F})$
is a torsion pair in
![]() $\mathscr {A}$
, then
$\mathscr {A}$
, then
![]() $\mathscr {T}$
is a functorially finite subcategory of
$\mathscr {T}$
is a functorially finite subcategory of
![]() $\mathscr {A}$
if and only if
$\mathscr {A}$
if and only if
![]() $\mathscr {F}$
is so. This is not true in an arbitrary abelian category with enough projective objects, as is shown by the following example.
$\mathscr {F}$
is so. This is not true in an arbitrary abelian category with enough projective objects, as is shown by the following example.
Example 2.4 Let
![]() $\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
. Set
$\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
. Set
 $$ \begin{align*} \mathscr{T}=&{\mathrm{add}}(\lbrace k_{[0, y)} \vert \ 0 < y\leq \infty\rbrace \cup \lbrace k_{[x, y)} \vert \ 1 \leq x< y\leq \infty\rbrace),\\ \mathscr{F}=&{\mathrm{add}}(\lbrace k_{[x, y)} \vert \ 0< x <y \leq 1\rbrace). \end{align*} $$
$$ \begin{align*} \mathscr{T}=&{\mathrm{add}}(\lbrace k_{[0, y)} \vert \ 0 < y\leq \infty\rbrace \cup \lbrace k_{[x, y)} \vert \ 1 \leq x< y\leq \infty\rbrace),\\ \mathscr{F}=&{\mathrm{add}}(\lbrace k_{[x, y)} \vert \ 0< x <y \leq 1\rbrace). \end{align*} $$
Then, by [Reference Bauer, Botnan, Oppermann and Steen7, Example 2.5],
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair. Obviously,
$(\mathscr {T}, \mathscr {F})$
is a torsion pair. Obviously,
![]() $\mathscr {T}$
is a functorially finite subcategory of
$\mathscr {T}$
is a functorially finite subcategory of
![]() $\mathscr {A}$
. We show that
$\mathscr {A}$
. We show that
![]() $\mathscr {F}$
is not a contravariantly finite subcategory of
$\mathscr {F}$
is not a contravariantly finite subcategory of
![]() $\mathscr {A}$
. To see this, note that objects such as
$\mathscr {A}$
. To see this, note that objects such as
![]() $K_{[0, b)}$
, where
$K_{[0, b)}$
, where
![]() $b<1$
, do not have a right
$b<1$
, do not have a right
![]() $\mathscr {F}$
-approximation. In fact, a right
$\mathscr {F}$
-approximation. In fact, a right
![]() $\mathscr {F}$
-approximation of
$\mathscr {F}$
-approximation of
![]() $K_{[0, b)}$
should be of the form
$K_{[0, b)}$
should be of the form
![]() $\theta : k_{[a, b)}\longrightarrow k_{[0, b)}$
, for some
$\theta : k_{[a, b)}\longrightarrow k_{[0, b)}$
, for some
![]() $0< a<b< 1$
. But nonzero morphisms such as
$0< a<b< 1$
. But nonzero morphisms such as
![]() $\eta : k_{[x, y)}\longrightarrow k_{[0, b)}$
, with
$\eta : k_{[x, y)}\longrightarrow k_{[0, b)}$
, with
![]() $0\leq x<a$
and
$0\leq x<a$
and
![]() $b\leq y$
, cannot factor through
$b\leq y$
, cannot factor through
![]() $\theta $
.
$\theta $
.
Definition 2.5 (See [Reference Salce31])
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. A pair
$\mathscr {A}$
be an abelian category with enough projective objects. A pair
![]() $(\mathscr {C}, \mathscr {D})$
of full subcategories of
$(\mathscr {C}, \mathscr {D})$
of full subcategories of
![]() $\mathscr {A}$
is called a cotorsion pair if
$\mathscr {A}$
is called a cotorsion pair if
![]() $\mathscr {C} = {}^{\perp _1}\mathscr {D}$
,
$\mathscr {C} = {}^{\perp _1}\mathscr {D}$
,
![]() $\mathscr {D} = \mathscr {C}^{\perp _1}$
and for every object
$\mathscr {D} = \mathscr {C}^{\perp _1}$
and for every object
![]() $A \in \mathscr {A}$
, there are short exact sequences
$A \in \mathscr {A}$
, there are short exact sequences
where C and
![]() $C'$
are in
$C'$
are in
![]() $\mathscr {C}$
and D and
$\mathscr {C}$
and D and
![]() $D'$
are in
$D'$
are in
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
This notion is sometimes called complete cotorsion pair in the literature. See [Reference Bauer, Botnan, Oppermann and Steen7, Remark 2.7] for more details.
Remark 2.6 It is immediate from the definition that in a cotorsion pair
![]() $(\mathscr {C}, \mathscr {D})$
both
$(\mathscr {C}, \mathscr {D})$
both
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
are closed under extensions.
$\mathscr {D}$
are closed under extensions.
Let
![]() $\mathscr {A}$
be an abelian category with enough projective and enough injective objects. In view of [Reference Beligiannis and Reiten11, Lemma V.3.3], a pair
$\mathscr {A}$
be an abelian category with enough projective and enough injective objects. In view of [Reference Beligiannis and Reiten11, Lemma V.3.3], a pair
![]() $(\mathscr {C}, \mathscr {D})$
of full subcategories of
$(\mathscr {C}, \mathscr {D})$
of full subcategories of
![]() $\mathscr {A}$
is a cotorsion pair if and only if the following conditions are satisfied:
$\mathscr {A}$
is a cotorsion pair if and only if the following conditions are satisfied:
-
1.
 $\mathscr {C} = {}^{\perp _1}\mathscr {D}$
,
$\mathscr {C} = {}^{\perp _1}\mathscr {D}$
, -
2. for every object
 $A \in \mathscr {A}$
, there exists a short exact sequence where
$A \in \mathscr {A}$
, there exists a short exact sequence where $$\begin{align*}0 \longrightarrow A \stackrel{f}\longrightarrow D \longrightarrow C \longrightarrow 0,\end{align*}$$
$$\begin{align*}0 \longrightarrow A \stackrel{f}\longrightarrow D \longrightarrow C \longrightarrow 0,\end{align*}$$
 $D \in \mathscr {D}$
and
$D \in \mathscr {D}$
and
 $C \in \mathscr {C}$
.
$C \in \mathscr {C}$
.
The following proposition shows that when
![]() $\mathscr {D}$
is closed under factors it is enough, in the above definition, to check Condition
$\mathscr {D}$
is closed under factors it is enough, in the above definition, to check Condition
![]() $2$
only for projective objects.
$2$
only for projective objects.
Proposition 2.7 Let
![]() $\mathscr {A}$
be an abelian category with enough projective and enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough projective and enough injective objects. Let
![]() $(\mathscr {C}, \mathscr {D})$
be a pair of full subcategories of
$(\mathscr {C}, \mathscr {D})$
be a pair of full subcategories of
![]() $\mathscr {A}$
such that
$\mathscr {A}$
such that
![]() $\mathscr {D}$
is closed under factors. Then
$\mathscr {D}$
is closed under factors. Then
![]() $(\mathscr {C}, \mathscr {D})$
is a cotorsion pair if and only if:
$(\mathscr {C}, \mathscr {D})$
is a cotorsion pair if and only if:
-
1.
 $\mathscr {C} = {}^{\perp _1}\mathscr {D}$
,
$\mathscr {C} = {}^{\perp _1}\mathscr {D}$
, -
2. for every projective object
 $P \in \mathscr {A}$
, there exists a short exact sequence where
$P \in \mathscr {A}$
, there exists a short exact sequence where $$\begin{align*}0 \longrightarrow P \stackrel{f}\longrightarrow D \longrightarrow C \longrightarrow 0,\end{align*}$$
$$\begin{align*}0 \longrightarrow P \stackrel{f}\longrightarrow D \longrightarrow C \longrightarrow 0,\end{align*}$$
 $D \in \mathscr {D}\cap \mathscr {C}$
and
$D \in \mathscr {D}\cap \mathscr {C}$
and
 $C \in \mathscr {C}$
.
$C \in \mathscr {C}$
.
Proof. We start by showing the necessity. Let A be an arbitrary object of
![]() $\mathscr {A}$
. Since
$\mathscr {A}$
. Since
![]() $\mathscr {A}$
has enough projective objects, we have an epimorphism
$\mathscr {A}$
has enough projective objects, we have an epimorphism
![]() $P \longrightarrow A \longrightarrow 0$
. By assumption, P fits into the short exact sequence
$P \longrightarrow A \longrightarrow 0$
. By assumption, P fits into the short exact sequence
The pushout diagram

induces the short exact sequence
![]() $0 \longrightarrow A \longrightarrow U \longrightarrow C \longrightarrow 0$
, where
$0 \longrightarrow A \longrightarrow U \longrightarrow C \longrightarrow 0$
, where
![]() $U \in {\mathrm {Fac}}(\mathscr {D})$
. Since
$U \in {\mathrm {Fac}}(\mathscr {D})$
. Since
![]() $\mathscr {D}$
is closed under factors, we deduce that
$\mathscr {D}$
is closed under factors, we deduce that
![]() $U \in \mathscr {D}$
, and hence this is the desired short exact sequence for A.
$U \in \mathscr {D}$
, and hence this is the desired short exact sequence for A.
For the sufficiency, let P be a projective object in
![]() $\mathscr {A}$
. Then there exists a short exact sequence
$\mathscr {A}$
. Then there exists a short exact sequence
where
![]() $D \in \mathscr {D}$
and
$D \in \mathscr {D}$
and
![]() $C \in \mathscr {C}$
. Since P is projective,
$C \in \mathscr {C}$
. Since P is projective,
![]() $P \in {}^{\perp _1}\mathscr {D} = \mathscr {C}$
. Hence,
$P \in {}^{\perp _1}\mathscr {D} = \mathscr {C}$
. Hence,
![]() $D \in \mathscr {C}$
because
$D \in \mathscr {C}$
because
![]() $\mathscr {C}$
is closed under extensions and the result follows.
$\mathscr {C}$
is closed under extensions and the result follows.
The proof of the following lemma is included in the proof of [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 2.28], but is restated here for convenience.
Lemma 2.8 Let
![]() $(\mathscr {C}, \mathscr {D})$
be a cotorsion pair in
$(\mathscr {C}, \mathscr {D})$
be a cotorsion pair in
![]() $\mathscr {A}$
such that
$\mathscr {A}$
such that
![]() $\mathscr {D}$
is a torsion class. Then
$\mathscr {D}$
is a torsion class. Then
![]() $\mathscr {C} \cap \mathscr {D}$
is a contravariantly finite subcategory of
$\mathscr {C} \cap \mathscr {D}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. Let
![]() $A \in \mathscr {A}$
be an arbitrary object. Since
$A \in \mathscr {A}$
be an arbitrary object. Since
![]() $\mathscr {D}$
is a torsion class, there exists a monomorphism
$\mathscr {D}$
is a torsion class, there exists a monomorphism
![]() $tA \longrightarrow A$
with
$tA \longrightarrow A$
with
![]() $tA \in \mathscr {D}$
. Since
$tA \in \mathscr {D}$
. Since
![]() $(\mathscr {C}, \mathscr {D})$
is a cotorsion pair, there exists a short exact sequence
$(\mathscr {C}, \mathscr {D})$
is a cotorsion pair, there exists a short exact sequence
such that
![]() $D \in \mathscr {D}$
and
$D \in \mathscr {D}$
and
![]() $C\in \mathscr {C}$
. Since
$C\in \mathscr {C}$
. Since
![]() $D, tA\in \mathscr {D}$
, and
$D, tA\in \mathscr {D}$
, and
![]() $\mathscr {D}$
is closed under extensions,
$\mathscr {D}$
is closed under extensions,
![]() $C \in \mathscr {C} \cap \mathscr {D}$
. We claim that the composition
$C \in \mathscr {C} \cap \mathscr {D}$
. We claim that the composition
![]() $C \stackrel {\imath }\longrightarrow tA\stackrel {\jmath }\longrightarrow A $
is a right
$C \stackrel {\imath }\longrightarrow tA\stackrel {\jmath }\longrightarrow A $
is a right
![]() $\mathscr {C} \cap \mathscr {D}$
-approximation of A. To prove the claim, let
$\mathscr {C} \cap \mathscr {D}$
-approximation of A. To prove the claim, let
![]() $X \stackrel {\ell }\longrightarrow A$
be a morphism with
$X \stackrel {\ell }\longrightarrow A$
be a morphism with
![]() $X \in \mathscr {C}\cap \mathscr {D}$
. Since
$X \in \mathscr {C}\cap \mathscr {D}$
. Since
![]() $X \in \mathscr {D}$
and every map from
$X \in \mathscr {D}$
and every map from
![]() $\mathscr {D}$
to A factors through
$\mathscr {D}$
to A factors through
![]() $tA$
, the morphism
$tA$
, the morphism
![]() $\ell $
factors through
$\ell $
factors through
![]() $\jmath $
. Now since
$\jmath $
. Now since
![]() $X \in \mathscr {C}$
and
$X \in \mathscr {C}$
and
![]() ${\mathrm {Ext}}^1_A(X, D)=0$
, the morphism
${\mathrm {Ext}}^1_A(X, D)=0$
, the morphism
![]() $\ell $
factors through
$\ell $
factors through
![]() $\jmath \imath $
. Hence, the claim is proved.
$\jmath \imath $
. Hence, the claim is proved.
Definition 2.9 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. A triple
$\mathscr {A}$
be an abelian category with enough projective objects. A triple
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
![]() $\mathscr {A}$
is called a cotorsion torsion triple if
$\mathscr {A}$
is called a cotorsion torsion triple if
![]() $(\mathscr {C}, \mathscr {T})$
is a cotorsion pair and
$(\mathscr {C}, \mathscr {T})$
is a cotorsion pair and
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair.
$(\mathscr {T}, \mathscr {F})$
is a torsion pair.
It has been recently shown in [Reference Bauer, Botnan, Oppermann and Steen7] that cotorsion torsion triples and tilting subcategories are closely related. Before stating the explicit relation between these two concepts, let us recall the definition of a tilting subcategory.
Definition 2.10 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. An additively closed subcategory
$\mathscr {A}$
be an abelian category with enough projective objects. An additively closed subcategory
![]() $\mathscr {T}$
of
$\mathscr {T}$
of
![]() $\mathscr {A}$
is called a tilting subcategory if:
$\mathscr {A}$
is called a tilting subcategory if:
-
(i)
 $\mathscr {T}$
is a contravariantly finite subcategory of
$\mathscr {T}$
is a contravariantly finite subcategory of
 $\mathscr {A}$
.
$\mathscr {A}$
. -
(ii)
 ${\mathrm {Ext}}^1_{\mathscr {A}}(T_1, T_2)=0$
, for all
${\mathrm {Ext}}^1_{\mathscr {A}}(T_1, T_2)=0$
, for all
 $T_1, T_2\in \mathscr {T}$
.
$T_1, T_2\in \mathscr {T}$
. -
(iii) Every object
 $T\in \mathscr {T}$
has projective dimension at most
$T\in \mathscr {T}$
has projective dimension at most
 $1$
.
$1$
. -
(iv) For every projective object P in
 $\mathscr {A}$
, there exists a short exact sequence with
$\mathscr {A}$
, there exists a short exact sequence with $$\begin{align*}0\longrightarrow P\stackrel{f}{\longrightarrow}T^0\longrightarrow T^1\longrightarrow 0\end{align*}$$
$$\begin{align*}0\longrightarrow P\stackrel{f}{\longrightarrow}T^0\longrightarrow T^1\longrightarrow 0\end{align*}$$
 $T^i\in \mathscr {T}$
.
$T^i\in \mathscr {T}$
.
If
![]() $\mathscr {T}$
satisfies only Conditions
$\mathscr {T}$
satisfies only Conditions
![]() $(ii)$
–
$(ii)$
–
![]() $(iv)$
, it is called a weak tilting subcategory of
$(iv)$
, it is called a weak tilting subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Theorem 2.11 (See [Reference Bauer, Botnan, Oppermann and Steen7, Theorem 2.29])
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Then there is a bijection
$\mathscr {A}$
be an abelian category with enough projective objects. Then there is a bijection
 $$\begin{align*}\lbrace \mbox{tilting subcategories}\rbrace &~~~~\longleftrightarrow~~~~ \lbrace \mbox{cotorsion torsion triples}\rbrace\\\mathscr {T}&~~~~\longrightarrow ~~~~~({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, \mathrm {Fac}(\mathscr {T}), \mathscr {T}^{\perp _0})\\\mathscr{C}\cap\mathscr{T}&~~~~\longleftarrow ~~~~(\mathscr{C}, \mathscr{T}, \mathscr{F}),\end{align*}$$
$$\begin{align*}\lbrace \mbox{tilting subcategories}\rbrace &~~~~\longleftrightarrow~~~~ \lbrace \mbox{cotorsion torsion triples}\rbrace\\\mathscr {T}&~~~~\longrightarrow ~~~~~({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, \mathrm {Fac}(\mathscr {T}), \mathscr {T}^{\perp _0})\\\mathscr{C}\cap\mathscr{T}&~~~~\longleftarrow ~~~~(\mathscr{C}, \mathscr{T}, \mathscr{F}),\end{align*}$$
where
![]() $\mathrm {Fac}(\mathscr {T})$
is the full subcategory of
$\mathrm {Fac}(\mathscr {T})$
is the full subcategory of
![]() $\mathscr {A}$
consisting of factors of objects in
$\mathscr {A}$
consisting of factors of objects in
![]() $\mathscr {T}$
.
$\mathscr {T}$
.
Remark 2.12 Note, as it is also mentioned in [Reference Bauer, Botnan, Oppermann and Steen7, Remark 1.9], that there is an extensive manuscript by Beligiannis [Reference Beligiannis10], started in 2004, in which he developed a fully general tilting theory in any abelian category without any assumption on enough projective or injective objects. Although the paper is not yet publicly available, the results of this work have been announced at several conferences in the subsequent years. Specifically, he has proved and announced a result similar to the theorem above in the more general setting of an arbitrary abelian category.
3
 $\tau $
-tilting subcategories
$\tau $
-tilting subcategories
In this section, we recall the definition of
![]() $\tau $
-tilting subcategories and study some of their properties. The following definition is motivated by [Reference Iyama, Jørgensen and Yang26, Definition 1.5] and [Reference Liu and Zhou28, Definition 2.1]. Note that for
$\tau $
-tilting subcategories and study some of their properties. The following definition is motivated by [Reference Iyama, Jørgensen and Yang26, Definition 1.5] and [Reference Liu and Zhou28, Definition 2.1]. Note that for
![]() $X\in \mathscr {A}$
, we let
$X\in \mathscr {A}$
, we let
![]() ${\mathrm {add}}(X)$
be the category of all direct summands of finite direct sums of copies of X.
${\mathrm {add}}(X)$
be the category of all direct summands of finite direct sums of copies of X.
Definition 3.1 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {T}$
be an additive full subcategory of
$\mathscr {T}$
be an additive full subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {T}$
is called a weak support
$\mathscr {T}$
is called a weak support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
if:
$\mathscr {A}$
if:
-
(i)
 ${\mathrm {Ext}}^1_{\mathscr {A}}(T_1,{\mathrm {Fac}}(T_2))=0,$
for all
${\mathrm {Ext}}^1_{\mathscr {A}}(T_1,{\mathrm {Fac}}(T_2))=0,$
for all
 $T_1, T_2 \in \mathscr {T}$
.
$T_1, T_2 \in \mathscr {T}$
. -
(ii) For any projective P in
 $\mathscr {A}$
, there exists an exact sequence such that
$\mathscr {A}$
, there exists an exact sequence such that $$\begin{align*}P \stackrel{f}{\longrightarrow} T^0 \longrightarrow T^1 \longrightarrow 0\end{align*}$$
$$\begin{align*}P \stackrel{f}{\longrightarrow} T^0 \longrightarrow T^1 \longrightarrow 0\end{align*}$$
 $T^0$
and
$T^0$
and
 $T^1$
are in
$T^1$
are in
 $\mathscr {T}$
and f is a left
$\mathscr {T}$
and f is a left
 $\mathscr {T}$
-approximation of P.
$\mathscr {T}$
-approximation of P.
If, furthermore,
![]() $\mathscr {T}$
is a contravariantly finite subcategory of
$\mathscr {T}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
, it is called a support
$\mathscr {A}$
, it is called a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. A support
$\mathscr {A}$
. A support
![]() $\tau $
-tilting subcategory is simply called
$\tau $
-tilting subcategory is simply called
![]() $\tau $
-tilting if the approximation
$\tau $
-tilting if the approximation
![]() $f: P \longrightarrow T^0$
is nonzero for every projective object P. An object
$f: P \longrightarrow T^0$
is nonzero for every projective object P. An object
![]() $T\in \mathscr {A}$
is called a support
$T\in \mathscr {A}$
is called a support
![]() $\tau $
-tilting object if
$\tau $
-tilting object if
![]() ${\mathrm {add}}(T)$
is a support
${\mathrm {add}}(T)$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Remark 3.2 We note that the previous definition is not the classical definition of support
![]() $\tau $
-tilting modules in
$\tau $
-tilting modules in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
introduced in [Reference Adachi, Iyama and Reiten1]. However, it follows from [Reference Jasso27, Proposition 2.14] that these two definitions coincide if
${\mathrm {{mod\mbox {-}}}}\Lambda $
introduced in [Reference Adachi, Iyama and Reiten1]. However, it follows from [Reference Jasso27, Proposition 2.14] that these two definitions coincide if
![]() $\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
.
$\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
.
A key difference between tilting and
![]() $\tau $
-tilting subcategories is that the approximations
$\tau $
-tilting subcategories is that the approximations
![]() $f: P \longrightarrow T^0$
are always a monomorphism when
$f: P \longrightarrow T^0$
are always a monomorphism when
![]() $\mathscr {T}$
is a tilting subcategory. It is immediate from the definition that every (weak) tilting subcategory is a (weak)
$\mathscr {T}$
is a tilting subcategory. It is immediate from the definition that every (weak) tilting subcategory is a (weak)
![]() $\tau $
-tilting subcategory. In the following example, we present a support
$\tau $
-tilting subcategory. In the following example, we present a support
![]() $\tau $
-tilting subcategory which is not a tilting subcategory.
$\tau $
-tilting subcategory which is not a tilting subcategory.
Example 3.3 Let
![]() $\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
, and set
$\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
, and set
Then
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory. To see this, first note that
$\tau $
-tilting subcategory. To see this, first note that
and obviously
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))=0$
.
${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))=0$
.
Now let
![]() $k_{[a, \infty )}$
be an indecomposable projective in
$k_{[a, \infty )}$
be an indecomposable projective in
![]() $\mathscr {A}$
. If
$\mathscr {A}$
. If
![]() $a\geq 1$
, the exact sequence
$a\geq 1$
, the exact sequence
and if
![]() $0\leq a< 1$
, the exact sequence
$0\leq a< 1$
, the exact sequence
are the desired exact sequences.
Moreover,
![]() $\mathscr {T}$
is a contravariantly finite subcategory of
$\mathscr {T}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
. Indeed, depending on a and b, for an indecomposable representation
$\mathscr {A}$
. Indeed, depending on a and b, for an indecomposable representation
![]() $k_{[ a, b)}$
, we have the following right
$k_{[ a, b)}$
, we have the following right
![]() $\mathscr {T}$
-approximations:
$\mathscr {T}$
-approximations:
 $$\begin{align*}\left\{ \begin{array}{r@{\ \,}cl} k_{[0, b)}&\longrightarrow k_{[0, b)}, & 0= a< b \leq 1,\\ k_{[1, \infty)}&\longrightarrow k_{[a, b)}, & 0\leq a< 1 < b \leq \infty,\\ 0&\longrightarrow k_{[a, b)}, & 0< a< b \leq 1,\\ k_{[a, \infty)}&\longrightarrow k_{[a, b)}, & 1\leq a < b\leq \infty. \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{r@{\ \,}cl} k_{[0, b)}&\longrightarrow k_{[0, b)}, & 0= a< b \leq 1,\\ k_{[1, \infty)}&\longrightarrow k_{[a, b)}, & 0\leq a< 1 < b \leq \infty,\\ 0&\longrightarrow k_{[a, b)}, & 0< a< b \leq 1,\\ k_{[a, \infty)}&\longrightarrow k_{[a, b)}, & 1\leq a < b\leq \infty. \end{array} \right. \end{align*}$$
It is not a tilting subcategory of
![]() $\mathscr {A}$
, because
$\mathscr {A}$
, because
![]() $k_{[0, \infty )}$
is a projective object, for which we do not have a short exact sequence like Condition
$k_{[0, \infty )}$
is a projective object, for which we do not have a short exact sequence like Condition
![]() $(iv)$
of Definition 2.10.
$(iv)$
of Definition 2.10.
One of the main reasons behind the success of
![]() $\tau $
-tilting theory [Reference Adachi, Iyama and Reiten1] is the formal inclusion of the notion of support from the start (see Definition 5.8). Note that in this definition we are defining objects in
$\tau $
-tilting theory [Reference Adachi, Iyama and Reiten1] is the formal inclusion of the notion of support from the start (see Definition 5.8). Note that in this definition we are defining objects in
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
by using a property of the object in a different category, namely
${\mathrm {{mod\mbox {-}}}} \Lambda $
by using a property of the object in a different category, namely
![]() ${\mathrm {{mod\mbox {-}}}} (\Lambda /\langle e\rangle )$
. So one needs to verify that the good properties of a support
${\mathrm {{mod\mbox {-}}}} (\Lambda /\langle e\rangle )$
. So one needs to verify that the good properties of a support
![]() $\tau $
-tilting object M in
$\tau $
-tilting object M in
![]() ${\mathrm {{mod\mbox {-}}}} (\Lambda /\langle e\rangle )$
can be transported to
${\mathrm {{mod\mbox {-}}}} (\Lambda /\langle e\rangle )$
can be transported to
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
. This was done in [Reference Adachi, Iyama and Reiten1, Lemma 2.1]. Note that
${\mathrm {{mod\mbox {-}}}} \Lambda $
. This was done in [Reference Adachi, Iyama and Reiten1, Lemma 2.1]. Note that
![]() ${\mathrm {{mod\mbox {-}}}} (\Lambda /\langle e\rangle )$
is a functorially finite wide subcategory of
${\mathrm {{mod\mbox {-}}}} (\Lambda /\langle e\rangle )$
is a functorially finite wide subcategory of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
which is at the same time a torsion and a torsion-free class. Recall that a subcategory
${\mathrm {{mod\mbox {-}}}} \Lambda $
which is at the same time a torsion and a torsion-free class. Recall that a subcategory
![]() $\mathscr {X}$
of an abelian category
$\mathscr {X}$
of an abelian category
![]() $\mathscr {A}$
is called a wide subcategory if it is closed under kernels, cokernels, and extensions. In particular, this implies that
$\mathscr {A}$
is called a wide subcategory if it is closed under kernels, cokernels, and extensions. In particular, this implies that
![]() $\mathscr {X}$
itself is an abelian category. It is known that a subcategory
$\mathscr {X}$
itself is an abelian category. It is known that a subcategory
![]() $\mathscr {X}$
of an abelian category
$\mathscr {X}$
of an abelian category
![]() $\mathscr {A}$
is a torsion class if it is a contravariantly finite subcategory of
$\mathscr {A}$
is a torsion class if it is a contravariantly finite subcategory of
![]() $\mathscr {A}$
, closed with respect to quotients and extensions. Similarly,
$\mathscr {A}$
, closed with respect to quotients and extensions. Similarly,
![]() $\mathscr {X}$
is a torsion-free class if it is a covariantly finite subcategory of
$\mathscr {X}$
is a torsion-free class if it is a covariantly finite subcategory of
![]() $\mathscr {A}$
which is furthermore closed under subobjects and extensions (see [Reference Beligiannis9, Proposition 2.1] and [Reference Dickson19, Theorem 2.3]).
$\mathscr {A}$
which is furthermore closed under subobjects and extensions (see [Reference Beligiannis9, Proposition 2.1] and [Reference Dickson19, Theorem 2.3]).
Lemma 3.4 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {X}$
be a wide and functorially finite full subcategory of
$\mathscr {X}$
be a wide and functorially finite full subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {X}$
is a torsion class of
$\mathscr {X}$
is a torsion class of
![]() $\mathscr {A}$
if and only if
$\mathscr {A}$
if and only if
![]() $\mathscr {X}$
is a torsion-free class of
$\mathscr {X}$
is a torsion-free class of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. Let
![]() $\mathscr {X}$
be a torsion class of
$\mathscr {X}$
be a torsion class of
![]() $\mathscr {A}$
. To show that it is a torsion-free class, we need to show that it is covariantly finite, closed under subobjects, and closed under extensions. By the assumption,
$\mathscr {A}$
. To show that it is a torsion-free class, we need to show that it is covariantly finite, closed under subobjects, and closed under extensions. By the assumption,
![]() $\mathscr {X}$
is a covariantly finite subcategory. It is closed under extensions, since
$\mathscr {X}$
is a covariantly finite subcategory. It is closed under extensions, since
![]() $\mathscr {X}$
is a torsion class. Moreover, it is closed under subobjects, since it is a wide subcategory. The other implication follows similarly.
$\mathscr {X}$
is a torsion class. Moreover, it is closed under subobjects, since it is a wide subcategory. The other implication follows similarly.
Our next result is inspired by [Reference Adachi, Iyama and Reiten1, Lemma 2.1], and it justifies the name of support
![]() $\tau $
-tilting subcategories.
$\tau $
-tilting subcategories.
Proposition 3.5 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {X}$
be a wide and functorially finite torsion class of
$\mathscr {X}$
be a wide and functorially finite torsion class of
![]() $\mathscr {A}$
. Then every support
$\mathscr {A}$
. Then every support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {X}$
is a support
$\mathscr {X}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {X}$
. First, we note that, since
$\mathscr {X}$
. First, we note that, since
![]() $\mathscr {X}$
is a wide subcategory, then
$\mathscr {X}$
is a wide subcategory, then
![]() ${\mathrm {Fac}}(\mathscr {T})\subseteq {\mathrm {Fac}}(\mathscr {X})=\mathscr {X}$
. Therefore, since
${\mathrm {Fac}}(\mathscr {T})\subseteq {\mathrm {Fac}}(\mathscr {X})=\mathscr {X}$
. Therefore, since
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {X}$
, we have
$\mathscr {X}$
, we have
![]() ${\mathrm {Ext}}^1_{\mathscr {X}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))=0$
. Hence,
${\mathrm {Ext}}^1_{\mathscr {X}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))=0$
. Hence,
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))=0$
.
${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))=0$
.
Now let P be a projective object in
![]() $\mathscr {A}$
. By Lemma 3.4, there is a subcategory
$\mathscr {A}$
. By Lemma 3.4, there is a subcategory
![]() $\mathscr {Y}$
of
$\mathscr {Y}$
of
![]() $\mathscr {A}$
such that
$\mathscr {A}$
such that
![]() $(\mathscr {Y}, \mathscr {X})$
is a torsion pair of
$(\mathscr {Y}, \mathscr {X})$
is a torsion pair of
![]() $\mathscr {A}$
. Consider the canonical short exact sequence
$\mathscr {A}$
. Consider the canonical short exact sequence
of P with respect to this torsion pair. So
![]() $Y \in \mathscr {Y}$
and
$Y \in \mathscr {Y}$
and
![]() $X \in \mathscr {X}$
. Let
$X \in \mathscr {X}$
. Let
![]() $X'$
be an arbitrary object of
$X'$
be an arbitrary object of
![]() $\mathscr {X}$
. By applying the functor
$\mathscr {X}$
. By applying the functor
![]() ${\mathrm {Hom}}_{\mathscr {A}}(-, X')$
to the above short exact sequence, we get
${\mathrm {Hom}}_{\mathscr {A}}(-, X')$
to the above short exact sequence, we get
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}(X, X')=0$
and therefore
${\mathrm {Ext}}^1_{\mathscr {A}}(X, X')=0$
and therefore
![]() ${\mathrm {Ext}}^1_{\mathscr {X}}(X, X')=0$
. Hence, X is an Ext-projective object in
${\mathrm {Ext}}^1_{\mathscr {X}}(X, X')=0$
. Hence, X is an Ext-projective object in
![]() $\mathscr {X}$
. Since
$\mathscr {X}$
. Since
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {X}$
, there exists an exact sequence
$\mathscr {X}$
, there exists an exact sequence
where
![]() $T^0, T^1\in \mathscr {T}$
and g is a left
$T^0, T^1\in \mathscr {T}$
and g is a left
![]() $\mathscr {T}$
-approximation. Now the exact sequence
$\mathscr {T}$
-approximation. Now the exact sequence
is the desired one. It is easy to see that
![]() $gf$
is a left
$gf$
is a left
![]() $\mathscr {T}$
-approximation of P.
$\mathscr {T}$
-approximation of P.
Finally, we show that
![]() $\mathscr {T}$
is a contravariantly finite subcategory of
$\mathscr {T}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
. Let
$\mathscr {A}$
. Let
![]() $A\in \mathscr {A}$
. Since
$A\in \mathscr {A}$
. Since
![]() $\mathscr {X}$
is a functorially finite subcategory of
$\mathscr {X}$
is a functorially finite subcategory of
![]() $\mathscr {A}$
, there exists a right
$\mathscr {A}$
, there exists a right
![]() $\mathscr {X}$
-approximation
$\mathscr {X}$
-approximation
![]() $X\stackrel {f}\longrightarrow A$
of A. Consider a right
$X\stackrel {f}\longrightarrow A$
of A. Consider a right
![]() $\mathscr {T}$
-approximation
$\mathscr {T}$
-approximation
![]() $T\stackrel {g}\longrightarrow X$
of X, which exists because
$T\stackrel {g}\longrightarrow X$
of X, which exists because
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. Now it is easy to see that
$\mathscr {A}$
. Now it is easy to see that
![]() $T\stackrel {fg}\longrightarrow A$
is a right
$T\stackrel {fg}\longrightarrow A$
is a right
![]() $\mathscr {T}$
-approximation of A.
$\mathscr {T}$
-approximation of A.
We illustrate our previous result with the following example.
Example 3.6 Let
![]() $\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
and
$\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
and
![]() $\mathscr {B}=\mathrm { Rep}^{\mathrm {fp}}_k\mathbb {R}_{\geq 1}$
. On one hand, since
$\mathscr {B}=\mathrm { Rep}^{\mathrm {fp}}_k\mathbb {R}_{\geq 1}$
. On one hand, since
![]() $\mathbb {R}_{\geq 0}$
and
$\mathbb {R}_{\geq 0}$
and
![]() $\mathbb {R}_{\geq 1}$
are isomorphic as posets, it is clear that
$\mathbb {R}_{\geq 1}$
are isomorphic as posets, it is clear that
![]() $\mathscr {A}$
and
$\mathscr {A}$
and
![]() $\mathscr {B}$
are equivalent as categories. On the other hand, the natural inclusion of
$\mathscr {B}$
are equivalent as categories. On the other hand, the natural inclusion of
![]() $\mathbb {R}_{\geq 1}$
into
$\mathbb {R}_{\geq 1}$
into
![]() $\mathbb {R}_{\geq 0}$
induces an embedding of
$\mathbb {R}_{\geq 0}$
induces an embedding of
![]() $\mathscr {B}$
into
$\mathscr {B}$
into
![]() $\mathscr {A}$
. In fact, it is easy to see that
$\mathscr {A}$
. In fact, it is easy to see that
![]() $\mathscr {B}$
is a functorially finite wide subcategory of
$\mathscr {B}$
is a functorially finite wide subcategory of
![]() $\mathscr {A}$
which is both a torsion and a torsion-free class. Set
$\mathscr {A}$
which is both a torsion and a torsion-free class. Set
It is easy to see that
![]() $\mathscr {T}$
is a tilting subcategory of
$\mathscr {T}$
is a tilting subcategory of
![]() $\mathscr {B}$
and hence a support
$\mathscr {B}$
and hence a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {B}$
. So, Proposition 3.5 implies that
$\mathscr {B}$
. So, Proposition 3.5 implies that
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. Note that
$\mathscr {A}$
. Note that
![]() $\mathscr {T}$
is not a tilting subcategory of
$\mathscr {T}$
is not a tilting subcategory of
![]() $\mathscr {A}$
since the
$\mathscr {A}$
since the
![]() $\mathscr {T}$
-approximation
$\mathscr {T}$
-approximation
![]() $f: k_{[0,\infty )} \to k_{[1,\infty )}$
is not a monomorphism; in fact, it is a zero morphism.
$f: k_{[0,\infty )} \to k_{[1,\infty )}$
is not a monomorphism; in fact, it is a zero morphism.
By [Reference Rundsveen30, Proposition 3.42], if
![]() $\mathscr {A}$
is an abelian category with enough projective objects such that
$\mathscr {A}$
is an abelian category with enough projective objects such that
![]() ${\mathrm {Prj}}(\mathscr {A})={\mathrm {add}}(P)$
, then for every tilting subcategory
${\mathrm {Prj}}(\mathscr {A})={\mathrm {add}}(P)$
, then for every tilting subcategory
![]() $\mathscr {T}$
of
$\mathscr {T}$
of
![]() $\mathscr {A}$
, there exists an object
$\mathscr {A}$
, there exists an object
![]() $T \in \mathscr {T}$
such that
$T \in \mathscr {T}$
such that
![]() $\mathscr {T} = {\mathrm {add}}(T)$
. In fact, T is a tilting object. Note that an object
$\mathscr {T} = {\mathrm {add}}(T)$
. In fact, T is a tilting object. Note that an object
![]() $T\in \mathscr {A}$
is called a tilting object if:
$T\in \mathscr {A}$
is called a tilting object if:
-
(i)
 ${\mathrm {Ext}}^1_{\mathscr {A}}(T, T)=0$
.
${\mathrm {Ext}}^1_{\mathscr {A}}(T, T)=0$
. -
(ii) Projective dimension of T is at most 1.
-
(iii) For every projective object
 $P\in \mathscr {A}$
, there exists a short exact sequence such that
$P\in \mathscr {A}$
, there exists a short exact sequence such that $$\begin{align*}0\longrightarrow P\longrightarrow T^0\longrightarrow T^1\longrightarrow 0\end{align*}$$
$$\begin{align*}0\longrightarrow P\longrightarrow T^0\longrightarrow T^1\longrightarrow 0\end{align*}$$
 $T^0, T^1\in {\mathrm {add}}(T)$
.
$T^0, T^1\in {\mathrm {add}}(T)$
.
We prove a version of this fact for
![]() $\tau $
-tilting subcategories.
$\tau $
-tilting subcategories.
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let T be a support
$\mathscr {A}$
be an abelian category with enough projective objects. Let T be a support
![]() $\tau $
-tilting object in
$\tau $
-tilting object in
![]() $\mathscr {A}$
. It follows directly from the definition that
$\mathscr {A}$
. It follows directly from the definition that
![]() ${\mathrm {add}}(T)$
is a weak support
${\mathrm {add}}(T)$
is a weak support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. The next proposition provides a partial converse.
$\mathscr {A}$
. The next proposition provides a partial converse.
Proposition 3.7 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects such that
$\mathscr {A}$
be an abelian category with enough projective objects such that
![]() ${\mathrm {Prj}}(\mathscr {A})={\mathrm {add}}(P)$
, for some object
${\mathrm {Prj}}(\mathscr {A})={\mathrm {add}}(P)$
, for some object
![]() $P\in \mathscr {A}$
. If
$P\in \mathscr {A}$
. If
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
, then there exists a support
$\mathscr {A}$
, then there exists a support
![]() $\tau $
-tilting object
$\tau $
-tilting object
![]() $T\in \mathscr {T}$
such that
$T\in \mathscr {T}$
such that
![]() ${\mathrm {Fac}}(\mathscr {T})={\mathrm {Fac}}(T)$
.
${\mathrm {Fac}}(\mathscr {T})={\mathrm {Fac}}(T)$
.
Proof. Consider the exact sequence
which exists, because
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory. We claim that
$\tau $
-tilting subcategory. We claim that
![]() ${\mathrm {Fac}}(T^0\oplus T^1)={\mathrm {Fac}}(\mathscr {T})$
. First, we prove that
${\mathrm {Fac}}(T^0\oplus T^1)={\mathrm {Fac}}(\mathscr {T})$
. First, we prove that
![]() $T^0\oplus T^1$
is a support
$T^0\oplus T^1$
is a support
![]() $\tau $
-tilting object. To this end, we just need to show that every projective object
$\tau $
-tilting object. To this end, we just need to show that every projective object
![]() $P'\in {\mathrm {Prj}} (\mathscr {A})={\mathrm {add}}(P)$
admits an exact sequence
$P'\in {\mathrm {Prj}} (\mathscr {A})={\mathrm {add}}(P)$
admits an exact sequence
where
![]() $f'$
is a left
$f'$
is a left
![]() ${\mathrm {add}}(T^0\oplus T^1)$
-approximation and
${\mathrm {add}}(T^0\oplus T^1)$
-approximation and
![]() $T^0_{P'} , T^1_{P'}\in {\mathrm {add}}(T^0\oplus T^1)$
. Since
$T^0_{P'} , T^1_{P'}\in {\mathrm {add}}(T^0\oplus T^1)$
. Since
![]() ${\mathrm {Prj}}(\mathscr {A})={\mathrm {add}}(P)$
, there exists a nonnegative integer n and projective object
${\mathrm {Prj}}(\mathscr {A})={\mathrm {add}}(P)$
, there exists a nonnegative integer n and projective object
![]() $Q\in {\mathrm {add}}(P)$
such that
$Q\in {\mathrm {add}}(P)$
such that
![]() $P'\oplus Q=P^n$
. So we get the exact sequence
$P'\oplus Q=P^n$
. So we get the exact sequence
Based on this sequence, we can construct the following commutative diagram:

Since the second vertical short exact sequence splits, both
![]() ${\mathrm {Coker}} g $
and
${\mathrm {Coker}} g $
and
![]() ${\mathrm {Coker}} h $
are in
${\mathrm {Coker}} h $
are in
![]() ${\mathrm {add}}(T_0\oplus T_1)$
. Therefore, the exact sequence
${\mathrm {add}}(T_0\oplus T_1)$
. Therefore, the exact sequence
is the desired one.
Now we show that
![]() ${\mathrm {Fac}}(\mathscr {T}) = {\mathrm {Fac}}(T^0\oplus T^1)$
. It is clear that
${\mathrm {Fac}}(\mathscr {T}) = {\mathrm {Fac}}(T^0\oplus T^1)$
. It is clear that
![]() ${\mathrm {Fac}}(T^0\oplus T^1)\subseteq {\mathrm {Fac}}(\mathscr {T})$
. So it is enough to show the reverse inclusion. To do this, we show that every object
${\mathrm {Fac}}(T^0\oplus T^1)\subseteq {\mathrm {Fac}}(\mathscr {T})$
. So it is enough to show the reverse inclusion. To do this, we show that every object
![]() $\bar {T}\in \mathscr {T}$
lies in
$\bar {T}\in \mathscr {T}$
lies in
![]() ${\mathrm {Fac}}(T^0\oplus T^1)$
. Let
${\mathrm {Fac}}(T^0\oplus T^1)$
. Let
be a projective presentation of
![]() $\bar {T}$
. Since
$\bar {T}$
. Since
![]() $T^0\oplus T^1$
is a support
$T^0\oplus T^1$
is a support
![]() $\tau $
-tilting object, for
$\tau $
-tilting object, for
![]() $i=0, 1$
, there are exact sequences
$i=0, 1$
, there are exact sequences
with
![]() $T^0_i , T^1_i\in {\mathrm {add}}(T_0\oplus T_1)$
. Therefore, since
$T^0_i , T^1_i\in {\mathrm {add}}(T_0\oplus T_1)$
. Therefore, since
![]() $f_i$
is a left
$f_i$
is a left
![]() ${\mathrm {add}}(T^0\oplus T^1)$
-approximation of
${\mathrm {add}}(T^0\oplus T^1)$
-approximation of
![]() $P_i$
, we have the commutative diagram
$P_i$
, we have the commutative diagram

where the first row and the first column are exact. Since
![]() $g_0k_1f_1=0$
and
$g_0k_1f_1=0$
and
![]() $k_0k_1f_1=0$
, by the cokernel property, we have morphisms
$k_0k_1f_1=0$
, by the cokernel property, we have morphisms
![]() $l_1: T^1_1\longrightarrow T^1_0$
and
$l_1: T^1_1\longrightarrow T^1_0$
and
![]() $l_0: T^1_1\longrightarrow \bar {T}$
such that
$l_0: T^1_1\longrightarrow \bar {T}$
such that
![]() $g_0k_1=l_1g_1$
and
$g_0k_1=l_1g_1$
and
![]() $l_0g_1=k_0k_1$
. To finish the proof, we show that the sequence
$l_0g_1=k_0k_1$
. To finish the proof, we show that the sequence

is exact. Indeed, let
![]() $x\oplus y\in T^1_0\oplus \bar {T}$
. Since
$x\oplus y\in T^1_0\oplus \bar {T}$
. Since
![]() $g_0$
is an epimorphism, there exists
$g_0$
is an epimorphism, there exists
![]() $t^{\prime }_0\in T^0_0$
such that
$t^{\prime }_0\in T^0_0$
such that
![]() $g_0(t^{\prime }_0)=x$
. Now since
$g_0(t^{\prime }_0)=x$
. Now since
![]() $h_0$
is an epimorphism, there exists
$h_0$
is an epimorphism, there exists
![]() $p_0\in P_0$
such that
$p_0\in P_0$
such that
![]() $h_0(p_0)=k_0(t^{\prime }_0)-y$
. Consider
$h_0(p_0)=k_0(t^{\prime }_0)-y$
. Consider
![]() $ (t^{\prime }_0-f_0(p_0))\oplus 0\in T^0_0\oplus T^1_1$
. Therefore, it is easy to see that
$ (t^{\prime }_0-f_0(p_0))\oplus 0\in T^0_0\oplus T^1_1$
. Therefore, it is easy to see that
 $$\begin{align*}{\begin{bmatrix} g_0\ l_0\\ k_0 \ l_1 \end{bmatrix}} \begin{bmatrix} t^{\prime}_0-f_0(p_0) \\ 0 \end{bmatrix} =\begin{bmatrix} x\\y \end{bmatrix}.\end{align*}$$
$$\begin{align*}{\begin{bmatrix} g_0\ l_0\\ k_0 \ l_1 \end{bmatrix}} \begin{bmatrix} t^{\prime}_0-f_0(p_0) \\ 0 \end{bmatrix} =\begin{bmatrix} x\\y \end{bmatrix}.\end{align*}$$
Hence,
![]() $\bar {T}\in {\mathrm {Fac}}(T^0_0\oplus T^1_1)\subseteq {\mathrm {Fac}}(T_0\oplus T_1)$
.
$\bar {T}\in {\mathrm {Fac}}(T^0_0\oplus T^1_1)\subseteq {\mathrm {Fac}}(T_0\oplus T_1)$
.
When
![]() $\mathscr {T}$
is a weak tilting subcategory of
$\mathscr {T}$
is a weak tilting subcategory of
![]() $\mathscr {A}$
, then
$\mathscr {A}$
, then
![]() ${\mathrm {Fac}}(\mathscr {T}) = \mathscr {T}^{\perp _1}$
(see [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 2.22]). The following example shows that this equality does not hold in general for
${\mathrm {Fac}}(\mathscr {T}) = \mathscr {T}^{\perp _1}$
(see [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 2.22]). The following example shows that this equality does not hold in general for
![]() $\tau $
-tilting subcategories.
$\tau $
-tilting subcategories.
Example 3.8 Let A be the path algebra of the quiver

modulo the ideal generated by all paths of length 2. The Auslander–Reiten quiver of A is

Let
![]() $\mathscr {T}={\mathrm {add}}({\tiny \begin {matrix}2\\ 3\end {matrix}}\oplus {{\tiny \begin {matrix}2\end {matrix}}} \oplus {{\tiny \begin {matrix}1\\ 2\end {matrix}}})$
. Then
$\mathscr {T}={\mathrm {add}}({\tiny \begin {matrix}2\\ 3\end {matrix}}\oplus {{\tiny \begin {matrix}2\end {matrix}}} \oplus {{\tiny \begin {matrix}1\\ 2\end {matrix}}})$
. Then
![]() $\mathscr {T}$
is a
$\mathscr {T}$
is a
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm {mod}\mbox {-}A$
. It is easy to see that
$\mathrm {mod}\mbox {-}A$
. It is easy to see that
4
 $\tau $
-cotorsion torsion triples
$\tau $
-cotorsion torsion triples
In this section, we introduce a triple of full additive subcategories of
![]() $\mathscr {A}$
, that will be called a
$\mathscr {A}$
, that will be called a
![]() $\tau $
-cotorsion torsion triple, or simply a
$\tau $
-cotorsion torsion triple, or simply a
![]() $\tau $
-triple, and show that there is a bijection between the collection of all
$\tau $
-triple, and show that there is a bijection between the collection of all
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathscr {A}$
and the collection of all
$\mathscr {A}$
and the collection of all
![]() $\tau $
-triples. Proposition 2.7 motivates the following definition.
$\tau $
-triples. Proposition 2.7 motivates the following definition.
Definition 4.1 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. A pair of full subcategories
$\mathscr {A}$
be an abelian category with enough projective objects. A pair of full subcategories
![]() $(\mathscr {C}, \mathscr {D})$
of
$(\mathscr {C}, \mathscr {D})$
of
![]() $\mathscr {A}$
is called a
$\mathscr {A}$
is called a
![]() $\tau $
-cotorsion pair if:
$\tau $
-cotorsion pair if:
-
1.
 $\mathscr {C} = {}^{\perp _1}\mathscr {D}$
.
$\mathscr {C} = {}^{\perp _1}\mathscr {D}$
. -
2. For every projective object
 $P \in \mathscr {A}$
, there exists an exact sequence where
$P \in \mathscr {A}$
, there exists an exact sequence where $$\begin{align*}P \stackrel{f}\longrightarrow {D}\longrightarrow C \longrightarrow 0,\end{align*}$$
$$\begin{align*}P \stackrel{f}\longrightarrow {D}\longrightarrow C \longrightarrow 0,\end{align*}$$
 $D \in \mathscr {C}\cap \mathscr {D}$
,
$D \in \mathscr {C}\cap \mathscr {D}$
,
 $C \in \mathscr {C}$
, and f is a left
$C \in \mathscr {C}$
, and f is a left
 $\mathscr {D}$
-approximation.
$\mathscr {D}$
-approximation.
-
3.
 $\mathscr {C}\cap \mathscr {D}$
is a contravariantly finite subcategory of
$\mathscr {C}\cap \mathscr {D}$
is a contravariantly finite subcategory of
 $\mathscr {A}$
.
$\mathscr {A}$
.
Example 4.2 Let
![]() $\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
and set
$\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
and set
 $$ \begin{align*} \mathscr{C}=&{\mathrm{add}}(\lbrace k_{[x, \infty)} \vert \ 0\leq x < \infty\rbrace \cup \lbrace k_{[x, y)} \vert \ 0 \leq x < y< 1\rbrace)\\ \mathscr{D}=&{\mathrm{add}}(\lbrace k_{[x, y)} \vert \ 1\leq x< y \leq \infty \rbrace). \end{align*} $$
$$ \begin{align*} \mathscr{C}=&{\mathrm{add}}(\lbrace k_{[x, \infty)} \vert \ 0\leq x < \infty\rbrace \cup \lbrace k_{[x, y)} \vert \ 0 \leq x < y< 1\rbrace)\\ \mathscr{D}=&{\mathrm{add}}(\lbrace k_{[x, y)} \vert \ 1\leq x< y \leq \infty \rbrace). \end{align*} $$
Then
![]() $(\mathscr {C}, \mathscr {D})$
is a
$(\mathscr {C}, \mathscr {D})$
is a
![]() $\tau $
-cotorsion pair. Note that it is not a cotorsion pair, because
$\tau $
-cotorsion pair. Note that it is not a cotorsion pair, because
![]() $\mathscr {D}$
does not contain the injective objects. To see it is a
$\mathscr {D}$
does not contain the injective objects. To see it is a
![]() $\tau $
-cotorsion pair, first note that
$\tau $
-cotorsion pair, first note that
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
. Indeed, every indecomposable representation
$\mathscr {A}$
. Indeed, every indecomposable representation
![]() $k_{[ a, b)}$
admits a right
$k_{[ a, b)}$
admits a right
![]() $\mathscr {C}\cap \mathscr {D}$
-approximation as follows:
$\mathscr {C}\cap \mathscr {D}$
-approximation as follows:
 $$\begin{align*}\left\{ \begin{array}{r@{\ \,}cl} k_{[a, \infty)}&\longrightarrow k_{[a, b)}, & 1\leq a < b\leq \infty,\\ k_{[1, \infty)}&\longrightarrow k_{[a, b)}, & 0< a< 1 < b \leq \infty,\\ 0&\longrightarrow k_{[a, b)}, & 0\leq a< b \leq 1. \end{array} \right. \end{align*}$$
$$\begin{align*}\left\{ \begin{array}{r@{\ \,}cl} k_{[a, \infty)}&\longrightarrow k_{[a, b)}, & 1\leq a < b\leq \infty,\\ k_{[1, \infty)}&\longrightarrow k_{[a, b)}, & 0< a< 1 < b \leq \infty,\\ 0&\longrightarrow k_{[a, b)}, & 0\leq a< b \leq 1. \end{array} \right. \end{align*}$$
Now let
![]() $k_{[a, \infty )}$
be an indecomposable projective in
$k_{[a, \infty )}$
be an indecomposable projective in
![]() $\mathscr {A}$
. If
$\mathscr {A}$
. If
![]() $a\geq 1$
, the exact sequence
$a\geq 1$
, the exact sequence
and if
![]() $a< 1$
, the exact sequence
$a< 1$
, the exact sequence
with
![]() $b\geq 1$
, are the desired exact sequences. Finally, it is straightforward to see that
$b\geq 1$
, are the desired exact sequences. Finally, it is straightforward to see that
![]() $\mathscr {C}={}^{\perp _1}\mathscr {D}$
.
$\mathscr {C}={}^{\perp _1}\mathscr {D}$
.
It is shown in [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 2.12] that if
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
are two subcategories of an abelian category
$\mathscr {D}$
are two subcategories of an abelian category
![]() $\mathscr {A}$
such that
$\mathscr {A}$
such that
-
(1)
 ${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {C}, \mathscr {D})=0$
,
${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {C}, \mathscr {D})=0$
, -
(2)
 $\mathscr {D}$
is closed under factor objects,
$\mathscr {D}$
is closed under factor objects, -
(3) for every object
 $A\in \mathscr {A}$
, there exists a short exact sequence
$A\in \mathscr {A}$
, there exists a short exact sequence
 $0 \longrightarrow A \stackrel {\varphi }\longrightarrow D \longrightarrow C \longrightarrow 0$
where
$0 \longrightarrow A \stackrel {\varphi }\longrightarrow D \longrightarrow C \longrightarrow 0$
where
 $D \in \mathscr {D}$
and
$D \in \mathscr {D}$
and
 $C \in \mathscr {C}$
,
$C \in \mathscr {C}$
,
then every object in
![]() $\mathscr {C}$
is of projective dimension at most 1. In particular, a cotorsion pair
$\mathscr {C}$
is of projective dimension at most 1. In particular, a cotorsion pair
![]() $(\mathscr {C}, \mathscr {T})$
satisfies all the above conditions when it is embedded in a cotorsion torsion triple
$(\mathscr {C}, \mathscr {T})$
satisfies all the above conditions when it is embedded in a cotorsion torsion triple
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
. So the projective dimension of every object in
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
. So the projective dimension of every object in
![]() $\mathscr {C}$
is at most 1.
$\mathscr {C}$
is at most 1.
The following example shows that the injectivity of the morphism
![]() $\varphi $
in Condition
$\varphi $
in Condition
![]() $(3)$
is essential. We note that this is implicit in the proof of [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 2.12]. Also, note that it follows automatically from the previous definition that the map
$(3)$
is essential. We note that this is implicit in the proof of [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 2.12]. Also, note that it follows automatically from the previous definition that the map
![]() $\varphi $
is a left
$\varphi $
is a left
![]() $\mathscr {D}$
-approximation.
$\mathscr {D}$
-approximation.
Example 4.3 Let A be the path algebra of the quiver
modulo the ideal generated by the composition of the two arrows. The Auslander–Reiten quiver of A is the following.

Let
![]() $\mathscr {T}={\mathrm {add}}({\tiny \begin {matrix}1\\ 2\end {matrix}}\oplus {\tiny \begin {matrix}1\end {matrix}}\oplus {\tiny \begin {matrix}{3}\end {matrix}})$
. It is easy to see that
$\mathscr {T}={\mathrm {add}}({\tiny \begin {matrix}1\\ 2\end {matrix}}\oplus {\tiny \begin {matrix}1\end {matrix}}\oplus {\tiny \begin {matrix}{3}\end {matrix}})$
. It is easy to see that
![]() $\mathscr {T}$
is a
$\mathscr {T}$
is a
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm {mod}\mbox {-}A$
. Then we have
$\mathrm {mod}\mbox {-}A$
. Then we have
 $$ \begin{align*} \mathscr{D} & = {\mathrm{Fac}}(\mathscr{T})={\mathrm{add}}({\tiny\begin{matrix}1\\ 2\end{matrix}}\oplus {\tiny\begin{matrix}{1}\end{matrix}}\oplus {\tiny\begin{matrix}{3}\end{matrix}}), \\ \mathscr{C} & ={}^{\perp_1}{\mathrm{Fac}}(\mathscr{T})={\mathrm{add}}({\tiny\begin{matrix}1\\ 2\end{matrix}}\oplus {\tiny\begin{matrix}{1}\end{matrix}}\oplus {\tiny\begin{matrix}{3}\end{matrix}}\oplus {\tiny\begin{matrix}2 \\ 3\end{matrix}}). \end{align*} $$
$$ \begin{align*} \mathscr{D} & = {\mathrm{Fac}}(\mathscr{T})={\mathrm{add}}({\tiny\begin{matrix}1\\ 2\end{matrix}}\oplus {\tiny\begin{matrix}{1}\end{matrix}}\oplus {\tiny\begin{matrix}{3}\end{matrix}}), \\ \mathscr{C} & ={}^{\perp_1}{\mathrm{Fac}}(\mathscr{T})={\mathrm{add}}({\tiny\begin{matrix}1\\ 2\end{matrix}}\oplus {\tiny\begin{matrix}{1}\end{matrix}}\oplus {\tiny\begin{matrix}{3}\end{matrix}}\oplus {\tiny\begin{matrix}2 \\ 3\end{matrix}}). \end{align*} $$
It is clear that
![]() ${\mathrm {Fac}}(\mathscr {T})$
is closed under factor modules. However, the object
${\mathrm {Fac}}(\mathscr {T})$
is closed under factor modules. However, the object
![]() ${\tiny \begin {matrix}{1}\end {matrix}} \in \mathscr {C}$
has projective dimension
${\tiny \begin {matrix}{1}\end {matrix}} \in \mathscr {C}$
has projective dimension
![]() $2$
.
$2$
.
Definition 4.4 A triple
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
![]() $\mathscr {A}$
is called a
$\mathscr {A}$
is called a
![]() $\tau $
-cotorsion torsion triple, or simply a
$\tau $
-cotorsion torsion triple, or simply a
![]() $\tau $
-triple, if
$\tau $
-triple, if
![]() $(\mathscr {C}, \mathscr {T})$
is a
$(\mathscr {C}, \mathscr {T})$
is a
![]() $\tau $
-cotorsion pair and
$\tau $
-cotorsion pair and
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair.
$(\mathscr {T}, \mathscr {F})$
is a torsion pair.
Example 4.5 Let
![]() $\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
and
$\mathscr {A}=\mathrm {Rep}^{\mathrm {fp}}_k \mathbb {R}_{\geq 0}$
and
![]() $(\mathscr {C}, \mathscr {D})$
be the
$(\mathscr {C}, \mathscr {D})$
be the
![]() $\tau $
-cotorsion pair as in Example 4.2. Since
$\tau $
-cotorsion pair as in Example 4.2. Since
![]() $\mathscr {D}$
is a contravariantly finite subcategory of
$\mathscr {D}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
which is closed under factors and extensions, it is a torsion class. Hence,
$\mathscr {A}$
which is closed under factors and extensions, it is a torsion class. Hence,
![]() $(\mathscr {C}, \mathscr {D}, \mathscr {D}^{\perp _0})$
is a
$(\mathscr {C}, \mathscr {D}, \mathscr {D}^{\perp _0})$
is a
![]() $\tau $
-triple.
$\tau $
-triple.
Proposition 4.6 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Then every cotorsion torsion triple
$\mathscr {A}$
be an abelian category with enough projective objects. Then every cotorsion torsion triple
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
in
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
in
![]() $\mathscr {A}$
is a
$\mathscr {A}$
is a
![]() $\tau $
-cotorsion torsion triple.
$\tau $
-cotorsion torsion triple.
Proof. Since
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair, it is enough to show that
$(\mathscr {T}, \mathscr {F})$
is a torsion pair, it is enough to show that
![]() $(\mathscr {C}, \mathscr {T})$
is a
$(\mathscr {C}, \mathscr {T})$
is a
![]() $\tau $
-cotorsion pair. Condition
$\tau $
-cotorsion pair. Condition
![]() $1$
of Definition 4.1 holds trivially. Now let P be a projective object in
$1$
of Definition 4.1 holds trivially. Now let P be a projective object in
![]() $\mathscr {A}$
and consider the short exact sequence
$\mathscr {A}$
and consider the short exact sequence
![]() $0\longrightarrow P \stackrel {f}\longrightarrow T \longrightarrow C\longrightarrow 0,$
in which
$0\longrightarrow P \stackrel {f}\longrightarrow T \longrightarrow C\longrightarrow 0,$
in which
![]() $T\in \mathscr {T}, C\in \mathscr {C}$
, and f is a left
$T\in \mathscr {T}, C\in \mathscr {C}$
, and f is a left
![]() $\mathscr {T}$
-approximation. It exists by definition of a cotorsion pair. To show the validity of Condition
$\mathscr {T}$
-approximation. It exists by definition of a cotorsion pair. To show the validity of Condition
![]() $2$
of Definition 4.1, we just need to show that
$2$
of Definition 4.1, we just need to show that
![]() $T\in \mathscr {C}\cap \mathscr {T}$
. This follows using the facts that
$T\in \mathscr {C}\cap \mathscr {T}$
. This follows using the facts that
![]() $P, C \in \mathscr {C}$
and
$P, C \in \mathscr {C}$
and
![]() $\mathscr {C}$
is closed under extensions. The contravariantly finiteness of
$\mathscr {C}$
is closed under extensions. The contravariantly finiteness of
![]() $\mathscr {C} \cap \mathscr {T}$
follows from Lemma 2.8.
$\mathscr {C} \cap \mathscr {T}$
follows from Lemma 2.8.
Proposition 4.7 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
![]() $\tau $
-triple in
$\tau $
-triple in
![]() $\mathscr {A}$
. Then, for every object
$\mathscr {A}$
. Then, for every object
![]() $A\in \mathscr {A}$
, there exists an exact sequence
$A\in \mathscr {A}$
, there exists an exact sequence
where
![]() $T\in \mathscr {T}$
,
$T\in \mathscr {T}$
,
![]() $C\in \mathscr {C}$
, and g is a left
$C\in \mathscr {C}$
, and g is a left
![]() $\mathscr {T}$
-approximation.
$\mathscr {T}$
-approximation.
Proof. Let A be an arbitrary object of
![]() $\mathscr {A}$
. Let
$\mathscr {A}$
. Let
![]() $P\stackrel {\pi }\longrightarrow A\longrightarrow 0$
be an epimorphism from a projective object in
$P\stackrel {\pi }\longrightarrow A\longrightarrow 0$
be an epimorphism from a projective object in
![]() $\mathscr {A}$
. By
$\mathscr {A}$
. By
![]() $(2)$
of Definition 4.1, we can construct the following pushout diagram, where
$(2)$
of Definition 4.1, we can construct the following pushout diagram, where
![]() $C,\tilde {C}\in \mathscr {C}\cap \mathscr {T}$
and f is a left
$C,\tilde {C}\in \mathscr {C}\cap \mathscr {T}$
and f is a left
![]() $\mathscr {T}$
-approximation:
$\mathscr {T}$
-approximation:

We show that the second row in the above diagram is the desired exact sequence. First, we note that
![]() $T\in \mathscr {T}$
, because
$T\in \mathscr {T}$
, because
![]() $T\in {\mathrm {Fac}}(\mathscr {T})$
and
$T\in {\mathrm {Fac}}(\mathscr {T})$
and
![]() $\mathscr {T}$
is closed under quotients. To complete the proof, it remains to show that
$\mathscr {T}$
is closed under quotients. To complete the proof, it remains to show that
![]() $g: A\longrightarrow T$
is a left
$g: A\longrightarrow T$
is a left
![]() $\mathscr {T}$
-approximation. Let
$\mathscr {T}$
-approximation. Let
![]() $h: A\longrightarrow T'$
be a morphism in
$h: A\longrightarrow T'$
be a morphism in
![]() $\mathscr {A}$
with
$\mathscr {A}$
with
![]() $T'\in \mathscr {T}$
. Since f is a left
$T'\in \mathscr {T}$
. Since f is a left
![]() $\mathscr {T}$
-approximation, there exists a morphism
$\mathscr {T}$
-approximation, there exists a morphism
![]() $l: C\longrightarrow T'$
such that
$l: C\longrightarrow T'$
such that
![]() $lf=h\pi $
. Thus, the pushout property implies the existence of the morphism
$lf=h\pi $
. Thus, the pushout property implies the existence of the morphism
![]() $t: T\longrightarrow T'$
such that the diagram
$t: T\longrightarrow T'$
such that the diagram

is commutative. In other words, we have that
![]() $tg\pi = h\pi $
. Since
$tg\pi = h\pi $
. Since
![]() $\pi : P \longrightarrow A$
is an epimorphism, we obtain that
$\pi : P \longrightarrow A$
is an epimorphism, we obtain that
![]() $tg=h$
. Hence, g is a left
$tg=h$
. Hence, g is a left
![]() $\mathscr {T}$
-approximation.
$\mathscr {T}$
-approximation.
Corollary 4.8 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
![]() $\tau $
-triple in
$\tau $
-triple in
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {T}$
is a functorially finite torsion class of
$\mathscr {T}$
is a functorially finite torsion class of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. The contravariantly finiteness of
![]() $\mathscr {T}$
follows from the fact that it is a torsion class and its covariantly finiteness follows from the previous proposition.
$\mathscr {T}$
follows from the fact that it is a torsion class and its covariantly finiteness follows from the previous proposition.
Remark 4.9 In case
![]() $\mathscr {A}={\mathrm {{mod\mbox {-}}}} \Lambda $
, where
$\mathscr {A}={\mathrm {{mod\mbox {-}}}} \Lambda $
, where
![]() $\Lambda $
is an Artin algebra, a generalization of the notion of a cotorsion pair, called a left weak cotorsion pair, is introduced and studied in [Reference Buan and Zhou16]. Based on Definition 0.2 of [Reference Buan and Zhou16], a pair
$\Lambda $
is an Artin algebra, a generalization of the notion of a cotorsion pair, called a left weak cotorsion pair, is introduced and studied in [Reference Buan and Zhou16]. Based on Definition 0.2 of [Reference Buan and Zhou16], a pair
![]() $(\mathscr {C}, \mathscr {D})$
of subcategories of
$(\mathscr {C}, \mathscr {D})$
of subcategories of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
is a left weak cotorsion pair if:
${\mathrm {{mod\mbox {-}}}} \Lambda $
is a left weak cotorsion pair if:
-
(1)
 ${\mathrm {Ext}}^1_{\Lambda }(\mathscr {C}, \mathscr {D})=0$
.
${\mathrm {Ext}}^1_{\Lambda }(\mathscr {C}, \mathscr {D})=0$
. -
(2) For every
 $M \in {\mathrm {{mod\mbox {-}}}} \Lambda $
, there are exact sequences and
$M \in {\mathrm {{mod\mbox {-}}}} \Lambda $
, there are exact sequences and $$\begin{align*}M \stackrel{f}{\longrightarrow} D \longrightarrow C \longrightarrow 0\end{align*}$$
such that
$$\begin{align*}M \stackrel{f}{\longrightarrow} D \longrightarrow C \longrightarrow 0\end{align*}$$
such that $$\begin{align*}0 \longrightarrow D' \longrightarrow C' \stackrel{g}{\longrightarrow} M \longrightarrow 0\end{align*}$$
$$\begin{align*}0 \longrightarrow D' \longrightarrow C' \stackrel{g}{\longrightarrow} M \longrightarrow 0\end{align*}$$
 $C, C' \in \mathscr {C}$
,
$C, C' \in \mathscr {C}$
,
 $D, D' \in \mathscr {D}$
, f is a left
$D, D' \in \mathscr {D}$
, f is a left
 $\mathscr {D}$
-approximation of M, and g is a right
$\mathscr {D}$
-approximation of M, and g is a right
 $\mathscr {C}$
-approximation of M.
$\mathscr {C}$
-approximation of M.
A triple
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
is called a left weak cotorsion torsion triple if
${\mathrm {{mod\mbox {-}}}}\Lambda $
is called a left weak cotorsion torsion triple if
![]() $(\mathscr {C}, \mathscr {T})$
is a left weak cotorsion pair and
$(\mathscr {C}, \mathscr {T})$
is a left weak cotorsion pair and
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair.
$(\mathscr {T}, \mathscr {F})$
is a torsion pair.
In the following theorem, we show that in the module category of an Artin algebra,
![]() $\tau $
-triples are exactly left weak cotorsion torsion triples.
$\tau $
-triples are exactly left weak cotorsion torsion triples.
Theorem 4.10 Let
![]() $\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
, where
$\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
, where
![]() $\Lambda $
is an Artin algebra. Then the triple
$\Lambda $
is an Artin algebra. Then the triple
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
of full subcategories in
![]() $\mathscr {A}$
is a
$\mathscr {A}$
is a
![]() $\tau $
-triple if and only if it is a left weak cotorsion torsion triple.
$\tau $
-triple if and only if it is a left weak cotorsion torsion triple.
Proof. First, let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
![]() $\tau $
-triple. Since
$\tau $
-triple. Since
![]() $(\mathscr {T}, \mathscr {F})$
is already a torsion pair, we just need to show that
$(\mathscr {T}, \mathscr {F})$
is already a torsion pair, we just need to show that
![]() $(\mathscr {C}, \mathscr {T})$
is a left weak cotorsion pair. Condition
$(\mathscr {C}, \mathscr {T})$
is a left weak cotorsion pair. Condition
![]() $(1)$
of the definition of a left weak cotorsion pair is followed by the first condition of the definition of
$(1)$
of the definition of a left weak cotorsion pair is followed by the first condition of the definition of
![]() $\tau $
-cotorsion pair. Also, for
$\tau $
-cotorsion pair. Also, for
![]() $M\in {\mathrm {{mod\mbox {-}}}}\Lambda $
, by Proposition 4.7, there is an exact sequence
$M\in {\mathrm {{mod\mbox {-}}}}\Lambda $
, by Proposition 4.7, there is an exact sequence
where
![]() $T\in \mathscr {T}$
,
$T\in \mathscr {T}$
,
![]() $C\in \mathscr {C}$
, and f is a left
$C\in \mathscr {C}$
, and f is a left
![]() $\mathscr {T}$
-approximation. Now, for
$\mathscr {T}$
-approximation. Now, for
![]() $M\in {\mathrm {{mod\mbox {-}}}}\Lambda $
, we construct a short exact sequence as in Condition
$M\in {\mathrm {{mod\mbox {-}}}}\Lambda $
, we construct a short exact sequence as in Condition
![]() $(2)$
of the definition of left weak cotorsion pairs. Let
$(2)$
of the definition of left weak cotorsion pairs. Let
![]() $P_1\stackrel {\beta }\longrightarrow P_0\longrightarrow M\longrightarrow 0$
be a projective presentation of M. By Condition
$P_1\stackrel {\beta }\longrightarrow P_0\longrightarrow M\longrightarrow 0$
be a projective presentation of M. By Condition
![]() $(2)$
of the definition of a
$(2)$
of the definition of a
![]() $\tau $
-cotorsion pair, for projective module
$\tau $
-cotorsion pair, for projective module
![]() $P_1$
, there exists an exact sequence
$P_1$
, there exists an exact sequence
![]() $P_1\stackrel {\alpha }\longrightarrow T\longrightarrow C\longrightarrow 0$
. Consider the pushout diagram:
$P_1\stackrel {\alpha }\longrightarrow T\longrightarrow C\longrightarrow 0$
. Consider the pushout diagram:

In view of the construction of pushouts in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
, we have the exact sequence
${\mathrm {{mod\mbox {-}}}}\Lambda $
, we have the exact sequence
 $$\begin{align*}P_1\stackrel{\phi=\begin{bmatrix} \alpha\\ \beta \end{bmatrix}}\longrightarrow T\oplus P_0\longrightarrow C'\longrightarrow 0,\end{align*}$$
$$\begin{align*}P_1\stackrel{\phi=\begin{bmatrix} \alpha\\ \beta \end{bmatrix}}\longrightarrow T\oplus P_0\longrightarrow C'\longrightarrow 0,\end{align*}$$
and therefore the short exact sequence
 $$\begin{align*}0\longrightarrow {\mathrm{Im}}\phi\stackrel{\varphi: \begin{bmatrix} \iota\\ \kappa \end{bmatrix}}\longrightarrow T\oplus P_0\longrightarrow C'\longrightarrow 0.\end{align*}$$
$$\begin{align*}0\longrightarrow {\mathrm{Im}}\phi\stackrel{\varphi: \begin{bmatrix} \iota\\ \kappa \end{bmatrix}}\longrightarrow T\oplus P_0\longrightarrow C'\longrightarrow 0.\end{align*}$$
Now let
![]() $\pi : P_1\longrightarrow {\mathrm {Im}}\varphi \longrightarrow 0$
and let
$\pi : P_1\longrightarrow {\mathrm {Im}}\varphi \longrightarrow 0$
and let
![]() $\psi :{\mathrm {Im}}\varphi \longrightarrow T'$
be a morphism with
$\psi :{\mathrm {Im}}\varphi \longrightarrow T'$
be a morphism with
![]() $T'\in \mathscr {T}$
. We show that
$T'\in \mathscr {T}$
. We show that
![]() $\psi $
factors through
$\psi $
factors through
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\alpha $
is a left
$\alpha $
is a left
![]() $\mathscr {T}$
-approximation, then there exists a morphism
$\mathscr {T}$
-approximation, then there exists a morphism
![]() $\gamma : T\longrightarrow T'$
such that
$\gamma : T\longrightarrow T'$
such that
![]() $\psi \pi =\gamma \alpha =\gamma \iota \pi $
. Thus,
$\psi \pi =\gamma \alpha =\gamma \iota \pi $
. Thus,
![]() $\psi =\gamma \iota $
. By applying the functor
$\psi =\gamma \iota $
. By applying the functor
![]() ${\mathrm {Hom}}_\Lambda (-,\mathscr {T})$
on the above short exact sequence and using the fact that
${\mathrm {Hom}}_\Lambda (-,\mathscr {T})$
on the above short exact sequence and using the fact that
![]() $T\oplus P_0\in \mathscr {C}$
, we get
$T\oplus P_0\in \mathscr {C}$
, we get
![]() $C'\in \mathscr {C}$
. Now since
$C'\in \mathscr {C}$
. Now since
![]() $\mathscr {T}$
is a torsion class, it is closed under quotients, and so we have
$\mathscr {T}$
is a torsion class, it is closed under quotients, and so we have
![]() ${\mathrm {Ker}} g\in \mathscr {T}$
. Therefore, the short exact sequence
${\mathrm {Ker}} g\in \mathscr {T}$
. Therefore, the short exact sequence
is the desired one.
Now we show the converse. Let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a left weak cotorsion torsion triple. Again since
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a left weak cotorsion torsion triple. Again since
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair, we just need to show that
$(\mathscr {T}, \mathscr {F})$
is a torsion pair, we just need to show that
![]() $(\mathscr {C}, \mathscr {T})$
is a
$(\mathscr {C}, \mathscr {T})$
is a
![]() $\tau $
-cotorsion pair. By [Reference Buan and Zhou16, Lemma 4.1], we have Condition
$\tau $
-cotorsion pair. By [Reference Buan and Zhou16, Lemma 4.1], we have Condition
![]() $(1)$
of the definition of
$(1)$
of the definition of
![]() $\tau $
-cotorsion pair. To conclude Condition
$\tau $
-cotorsion pair. To conclude Condition
![]() $(2)$
of the definition of
$(2)$
of the definition of
![]() $\tau $
-cotorsion pair, we note that
$\tau $
-cotorsion pair, we note that
![]() $\mathscr {T}$
is a functorially finite torsion class and by [Reference Auslander and Smalø6] there exists an exact sequence
$\mathscr {T}$
is a functorially finite torsion class and by [Reference Auslander and Smalø6] there exists an exact sequence
where f is a left
![]() $\mathscr {T}$
-approximation,
$\mathscr {T}$
-approximation,
![]() $T\in \mathscr {T}\cap \mathscr {C}$
, and
$T\in \mathscr {T}\cap \mathscr {C}$
, and
![]() $C\in \mathscr {C}$
. Finally, Condition
$C\in \mathscr {C}$
. Finally, Condition
![]() $(3)$
of the definition of
$(3)$
of the definition of
![]() $\tau $
-cotorsion pairs follows by [Reference Buan and Zhou16, Theorem 0.4].
$\tau $
-cotorsion pairs follows by [Reference Buan and Zhou16, Theorem 0.4].
5
 $\tau $
-tilting subcategories and
$\tau $
-tilting subcategories and
 $\tau $
-triples
$\tau $
-triples
In this section, we show that there is a bijection between the collection of all support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathscr {A}$
and the collection of all
$\mathscr {A}$
and the collection of all
![]() $\tau $
-cotorsion torsion triples in
$\tau $
-cotorsion torsion triples in
![]() $\mathscr {A}$
. In case we start with a tilting subcategory, this bijection specializes to the one introduced in [Reference Bauer, Botnan, Oppermann and Steen7, Theorem 2.29]. We prepare the ground with some preliminary results.
$\mathscr {A}$
. In case we start with a tilting subcategory, this bijection specializes to the one introduced in [Reference Bauer, Botnan, Oppermann and Steen7, Theorem 2.29]. We prepare the ground with some preliminary results.
Lemma 5.1 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() ${}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}) \cap {\mathrm {Fac}}(\mathscr {T})=\mathscr {T}$
.
${}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}) \cap {\mathrm {Fac}}(\mathscr {T})=\mathscr {T}$
.
Proof. Since
![]() $\mathscr {A}$
is an abelian category with enough projectives
$\mathscr {A}$
is an abelian category with enough projectives
![]() ${\mathrm {Prj}}(\mathscr {A})$
, we have
${\mathrm {Prj}}(\mathscr {A})$
, we have
![]() $\mathscr {A}\simeq {\mathrm {{mod\mbox {-}}}}{\mathrm {Prj}}(\mathscr {A})$
, where
$\mathscr {A}\simeq {\mathrm {{mod\mbox {-}}}}{\mathrm {Prj}}(\mathscr {A})$
, where
![]() ${\mathrm {{mod\mbox {-}}}}{\mathrm {Prj}}(\mathscr {A})$
is the category of finitely presented functors on
${\mathrm {{mod\mbox {-}}}}{\mathrm {Prj}}(\mathscr {A})$
is the category of finitely presented functors on
![]() ${\mathrm {Prj}}(\mathscr {A})$
(see [Reference Beligiannis8, Corollaries 3.9 and 3.10]). Now the result follows by the part
${\mathrm {Prj}}(\mathscr {A})$
(see [Reference Beligiannis8, Corollaries 3.9 and 3.10]). Now the result follows by the part
![]() $(ii)$
of the proof of [Reference Iyama, Jørgensen and Yang26, Proposition 5.3].
$(ii)$
of the proof of [Reference Iyama, Jørgensen and Yang26, Proposition 5.3].
Proposition 5.2 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
is a
![]() $\tau $
-cotorsion pair.
$\tau $
-cotorsion pair.
Proof. The first condition of Definition 4.1 holds trivially. For the second condition, consider the exact sequence
where f is a left
![]() $\mathscr {T}$
-approximation of P and
$\mathscr {T}$
-approximation of P and
![]() $T^0, T^1\in \mathscr {T}$
, which exists for every projective object P. Now, by Lemma 5.1, we observe that
$T^0, T^1\in \mathscr {T}$
, which exists for every projective object P. Now, by Lemma 5.1, we observe that
![]() $T^0, T^1\in {}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}) \cap {\mathrm {Fac}}(\mathscr {T})$
. So it remains to show that f is a left
$T^0, T^1\in {}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}) \cap {\mathrm {Fac}}(\mathscr {T})$
. So it remains to show that f is a left
![]() ${\mathrm {Fac}}(\mathscr {T})$
-approximation of P. To show this, let
${\mathrm {Fac}}(\mathscr {T})$
-approximation of P. To show this, let
![]() $X\in {\mathrm {Fac}}(\mathscr {T})$
and let
$X\in {\mathrm {Fac}}(\mathscr {T})$
and let
![]() $g: P\longrightarrow X$
be a morphism. Consider an epimorphism
$g: P\longrightarrow X$
be a morphism. Consider an epimorphism
![]() $\pi :T\longrightarrow X$
with
$\pi :T\longrightarrow X$
with
![]() $T\in \mathscr {T}$
. Since P is a projective object, there is a morphism
$T\in \mathscr {T}$
. Since P is a projective object, there is a morphism
![]() $h: P\longrightarrow T$
such that
$h: P\longrightarrow T$
such that
![]() $\pi h=g$
. Now, because f is a left
$\pi h=g$
. Now, because f is a left
![]() $\mathscr {T}$
-approximation, there is a morphism
$\mathscr {T}$
-approximation, there is a morphism
![]() $t: T^0\longrightarrow T$
such that
$t: T^0\longrightarrow T$
such that
![]() $tf=h$
. Therefore, a morphism
$tf=h$
. Therefore, a morphism
![]() $\pi t: T^0\longrightarrow X$
exists such that
$\pi t: T^0\longrightarrow X$
exists such that
![]() $\pi t f=\pi h=g$
. Finally, Lemma 5.1 implies that
$\pi t f=\pi h=g$
. Finally, Lemma 5.1 implies that
![]() ${}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}) \cap {\mathrm {Fac}}(\mathscr {T})=\mathscr {T}$
is a contravariantly finite subcategory of
${}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}) \cap {\mathrm {Fac}}(\mathscr {T})=\mathscr {T}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
By [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 2.22], if
![]() $\mathscr {T}$
is a tilting subcategory of
$\mathscr {T}$
is a tilting subcategory of
![]() $\mathscr {A}$
, then the pair
$\mathscr {A}$
, then the pair
![]() $({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a torsion pair. We use the same technique to prove the same result for
$({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a torsion pair. We use the same technique to prove the same result for
![]() $\tau $
-tilting subcategories.
$\tau $
-tilting subcategories.
Proposition 5.3 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. If
$\mathscr {A}$
be an abelian category with enough projective objects. If
![]() ${\mathscr {T}\subseteq \mathscr {A}}$
is a
${\mathscr {T}\subseteq \mathscr {A}}$
is a
![]() $\tau $
-tilting subcategory, then
$\tau $
-tilting subcategory, then
![]() $({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a torsion pair.
$({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a torsion pair.
Proof. Let
![]() $X\in {\mathrm {Fac}}(\mathscr {T})$
. Then there exists an epimorphism
$X\in {\mathrm {Fac}}(\mathscr {T})$
. Then there exists an epimorphism
![]() $\mathscr {T}\longrightarrow X\longrightarrow 0$
with
$\mathscr {T}\longrightarrow X\longrightarrow 0$
with
![]() $T\in \mathscr {T}$
. The exact sequence
$T\in \mathscr {T}$
. The exact sequence
![]() $0\longrightarrow {\mathrm {Hom}}_{\mathscr {A}}(X, Y)\longrightarrow {\mathrm {Hom}}_{\mathscr {A}}(T, Y)$
shows that
$0\longrightarrow {\mathrm {Hom}}_{\mathscr {A}}(X, Y)\longrightarrow {\mathrm {Hom}}_{\mathscr {A}}(T, Y)$
shows that
![]() ${\mathrm {Hom}}_{\mathscr {A}}(X, Y)=0$
whenever
${\mathrm {Hom}}_{\mathscr {A}}(X, Y)=0$
whenever
![]() $Y\in \mathscr {T}^{\perp _0}$
.
$Y\in \mathscr {T}^{\perp _0}$
.
Now let
![]() $A\in \mathscr {A}$
be an arbitrary object. Since
$A\in \mathscr {A}$
be an arbitrary object. Since
![]() $\mathscr {T}$
is contravariantly finite subcategory, there exists a right
$\mathscr {T}$
is contravariantly finite subcategory, there exists a right
![]() $\mathscr {T}$
-approximation
$\mathscr {T}$
-approximation
![]() $\varphi : T\longrightarrow A$
. Consider the short exact sequence
$\varphi : T\longrightarrow A$
. Consider the short exact sequence
where
![]() ${\mathrm {Im}} \varphi \in {\mathrm {Fac}}(\mathscr {T})$
. By applying the functor
${\mathrm {Im}} \varphi \in {\mathrm {Fac}}(\mathscr {T})$
. By applying the functor
![]() ${\mathrm {Hom}}_{\mathscr {A}}(\mathscr {T}, -)$
, we have a long exact sequence
${\mathrm {Hom}}_{\mathscr {A}}(\mathscr {T}, -)$
, we have a long exact sequence
 $$\begin{align*}0&\longrightarrow {\mathrm{Hom}}_{\mathscr{A}}(-, {\mathrm{Im}}\varphi)\vert_{\mathscr{T}}\stackrel{f_*} \longrightarrow {\mathrm{Hom}}_{\mathscr{A}}(-, A)\vert_{\mathscr{T}} \longrightarrow {\mathrm{Hom}}_{\mathscr{A}}(-, {\mathrm{Coker}} \varphi)\vert_{\mathscr{T}}\\&\quad \longrightarrow {\mathrm{Ext}}^1_{\mathscr{A}}(-, {\mathrm{Im}} \varphi)\vert_{\mathscr{T}}.\end{align*}$$
$$\begin{align*}0&\longrightarrow {\mathrm{Hom}}_{\mathscr{A}}(-, {\mathrm{Im}}\varphi)\vert_{\mathscr{T}}\stackrel{f_*} \longrightarrow {\mathrm{Hom}}_{\mathscr{A}}(-, A)\vert_{\mathscr{T}} \longrightarrow {\mathrm{Hom}}_{\mathscr{A}}(-, {\mathrm{Coker}} \varphi)\vert_{\mathscr{T}}\\&\quad \longrightarrow {\mathrm{Ext}}^1_{\mathscr{A}}(-, {\mathrm{Im}} \varphi)\vert_{\mathscr{T}}.\end{align*}$$
Now, since f is a right
![]() $\mathscr {T}$
-approximation,
$\mathscr {T}$
-approximation,
![]() $f_*$
is an epimorphism. Also, since
$f_*$
is an epimorphism. Also, since
![]() $\mathscr {T}$
is
$\mathscr {T}$
is
![]() $\tau $
-tilting and
$\tau $
-tilting and
![]() ${\mathrm {Im}}\varphi \in {\mathrm {Fac}}(\mathscr {T})$
,
${\mathrm {Im}}\varphi \in {\mathrm {Fac}}(\mathscr {T})$
,
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}(-, {\mathrm {Im}} \varphi )\vert _{\mathscr {T}}=0$
. So
${\mathrm {Ext}}^1_{\mathscr {A}}(-, {\mathrm {Im}} \varphi )\vert _{\mathscr {T}}=0$
. So
![]() ${\mathrm {Hom}}_{\mathscr {A}}(-, {\mathrm {Coker}} \varphi )\vert _{\mathscr {T}}=0$
and hence
${\mathrm {Hom}}_{\mathscr {A}}(-, {\mathrm {Coker}} \varphi )\vert _{\mathscr {T}}=0$
and hence
![]() ${\mathrm {Coker}}\varphi \in \mathscr {T}^{\perp _0}$
.
${\mathrm {Coker}}\varphi \in \mathscr {T}^{\perp _0}$
.
As a consequence of this proposition, we obtain the following corollary. This is a generalization of [Reference Adachi, Iyama and Reiten1, Theorem 2.7], which proves the same result for the case when
![]() $\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
, the category of finitely generated modules over an Artin algebra
$\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
, the category of finitely generated modules over an Artin algebra
![]() $\Lambda $
.
$\Lambda $
.
Corollary 5.4 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() ${\mathrm {Fac}}(\mathscr {T})$
is a functorially finite torsion class of
${\mathrm {Fac}}(\mathscr {T})$
is a functorially finite torsion class of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. By Propositions 5.2 and 5.3,
![]() $({}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}), {\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a
$({}^{\perp _1} {\mathrm {Fac}}(\mathscr {T}), {\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a
![]() $\tau $
-cotorsion torsion triple. So the result follows from Corollary 4.8.
$\tau $
-cotorsion torsion triple. So the result follows from Corollary 4.8.
Lemma 5.5 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
![]() $\tau $
-cotorsion torsion triple in
$\tau $
-cotorsion torsion triple in
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {C}\cap \mathscr {T}$
is a support
$\mathscr {C}\cap \mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. First, we observe that, by the definition of
![]() $\tau $
-cotorsion torsion triples,
$\tau $
-cotorsion torsion triples,
![]() $\mathscr {C}\cap \mathscr {T}$
is a contravariantly finite subcategory of
$\mathscr {C}\cap \mathscr {T}$
is a contravariantly finite subcategory of
![]() $\mathscr {A}$
and
$\mathscr {A}$
and
Moreover, for every projective object P, there is an exact sequence
where
![]() $T, T' \in \mathscr {C} \cap \mathscr {T}$
and f is a left
$T, T' \in \mathscr {C} \cap \mathscr {T}$
and f is a left
![]() $\mathscr {T}$
-approximation. To verify the last condition of support
$\mathscr {T}$
-approximation. To verify the last condition of support
![]() $\mathscr {T}$
-tilting subcategories, it is enough to note that the left
$\mathscr {T}$
-tilting subcategories, it is enough to note that the left
![]() $\mathscr {T}$
-approximation f is also a left
$\mathscr {T}$
-approximation f is also a left
![]() $\mathscr {C}\cap \mathscr {T}$
-approximation.
$\mathscr {C}\cap \mathscr {T}$
-approximation.
Lemma 5.6 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
![]() $\tau $
-cotorsion torsion triple in
$\tau $
-cotorsion torsion triple in
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {T}={\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})$
.
$\mathscr {T}={\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})$
.
Proof. Since
![]() $\mathscr {T}$
is closed under factors, we observe that
$\mathscr {T}$
is closed under factors, we observe that
![]() ${\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})\subseteq \mathscr {T}$
. Now let
${\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})\subseteq \mathscr {T}$
. Now let
![]() $T\in \mathscr {T}$
and
$T\in \mathscr {T}$
and
![]() $P\stackrel {\pi }\longrightarrow T\longrightarrow 0$
be an epimorphism with projective object P. By Condition
$P\stackrel {\pi }\longrightarrow T\longrightarrow 0$
be an epimorphism with projective object P. By Condition
![]() $(2)$
of Definition 4.1, there is a left
$(2)$
of Definition 4.1, there is a left
![]() $\mathscr {T}$
-approximation
$\mathscr {T}$
-approximation
![]() $f: P\longrightarrow T'$
, where
$f: P\longrightarrow T'$
, where
![]() $T' \in \mathscr {C}\cap \mathscr {T}$
. So there exists an epimorphism
$T' \in \mathscr {C}\cap \mathscr {T}$
. So there exists an epimorphism
![]() $g: T' \longrightarrow T$
such that
$g: T' \longrightarrow T$
such that
![]() $gf=\pi $
. Hence,
$gf=\pi $
. Hence,
![]() $T \in {\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})$
.
$T \in {\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})$
.
Theorem 5.7 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Then there exists a bijection between the collection of all support
$\mathscr {A}$
be an abelian category with enough projective objects. Then there exists a bijection between the collection of all support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathscr {A}$
and the collections of all
$\mathscr {A}$
and the collections of all
![]() $\tau $
-cotorsion torsion triples in
$\tau $
-cotorsion torsion triples in
![]() $\mathscr {A}$
. This bijection is induced by the following maps:
$\mathscr {A}$
. This bijection is induced by the following maps:
 $$\begin{align*}\lbrace \mbox{support } \tau\mbox{-tilting subcategories}\rbrace ~~~~&\longleftrightarrow~~~~ \lbrace \tau\mbox{-cotorsion torsion triples}\rbrace\\\mathscr {T}~~~~&\stackrel {\Phi }\longrightarrow ~~~~~({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, \mathrm {Fac}(\mathscr {T}), \mathscr {T}^{\perp _0})\\\mathscr{C}\cap\mathscr{T}~~&\stackrel{\Psi}\longleftarrow ~~~(\mathscr{C}, \mathscr{T}, \mathscr{F})\qquad\qquad\qquad\qquad\end{align*}$$
$$\begin{align*}\lbrace \mbox{support } \tau\mbox{-tilting subcategories}\rbrace ~~~~&\longleftrightarrow~~~~ \lbrace \tau\mbox{-cotorsion torsion triples}\rbrace\\\mathscr {T}~~~~&\stackrel {\Phi }\longrightarrow ~~~~~({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, \mathrm {Fac}(\mathscr {T}), \mathscr {T}^{\perp _0})\\\mathscr{C}\cap\mathscr{T}~~&\stackrel{\Psi}\longleftarrow ~~~(\mathscr{C}, \mathscr{T}, \mathscr{F})\qquad\qquad\qquad\qquad\end{align*}$$
that are well-defined and mutually inverse. Moreover, this bijection restricts to the bijection between the collection of all tilting subcategories of
![]() $\mathscr {A}$
and the collections of all cotorsion torsion triples in
$\mathscr {A}$
and the collections of all cotorsion torsion triples in
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proof. It follows from Propositions 5.2 and 5.3 and Lemma 5.5 that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are well defined. We show that they are mutually inverse. Let
$\Psi $
are well defined. We show that they are mutually inverse. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory. We have that
$\tau $
-tilting subcategory. We have that
![]() $\mathscr {T} = {}^{\perp _1}({\mathrm {Fac}}(\mathscr {T}))\cap {\mathrm {Fac}}(\mathscr {T})$
by Lemma 5.1. Thus,
$\mathscr {T} = {}^{\perp _1}({\mathrm {Fac}}(\mathscr {T}))\cap {\mathrm {Fac}}(\mathscr {T})$
by Lemma 5.1. Thus,
![]() $\Psi \Phi \cong 1$
.
$\Psi \Phi \cong 1$
.
Now let
![]() $(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
$(\mathscr {C}, \mathscr {T}, \mathscr {F})$
be a
![]() $\tau $
-cotorsion torsion triple. First, we note that by Lemma 5.6,
$\tau $
-cotorsion torsion triple. First, we note that by Lemma 5.6,
![]() $\mathscr {T}={\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})$
and so
$\mathscr {T}={\mathrm {Fac}}(\mathscr {C}\cap \mathscr {T})$
and so
![]() $\mathscr {C}={}^{\perp _1}{\mathscr {T}}={}^{\perp _1} ({\mathrm {Fac}} (\mathscr {C}\cap \mathscr {T}))$
. Also, we have
$\mathscr {C}={}^{\perp _1}{\mathscr {T}}={}^{\perp _1} ({\mathrm {Fac}} (\mathscr {C}\cap \mathscr {T}))$
. Also, we have
![]() $\mathscr {F}=(\mathscr {C}\cap \mathscr {T})^{\perp _0}$
. Hence,
$\mathscr {F}=(\mathscr {C}\cap \mathscr {T})^{\perp _0}$
. Hence,
![]() $\Phi \Psi \cong 1$
and so the first statement holds.
$\Phi \Psi \cong 1$
and so the first statement holds.
We now prove that this bijection restricts to the bijection between cotorsion torsion triples in
![]() $\mathscr {A}$
and tilting subcategories in
$\mathscr {A}$
and tilting subcategories in
![]() $\mathscr {A}$
. Let
$\mathscr {A}$
. Let
![]() $\mathscr {T}$
be a tilting subcategory. We show that the
$\mathscr {T}$
be a tilting subcategory. We show that the
![]() $\tau $
-triple
$\tau $
-triple
is a cotorsion torsion triple. To see this, it is enough to show that
![]() $({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, \mathrm {Fac}(\mathscr {T}))$
is a cotorsion pair. First, we note that, since
$({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, \mathrm {Fac}(\mathscr {T}))$
is a cotorsion pair. First, we note that, since
![]() $\mathscr {T}$
is a tilting subcategory of
$\mathscr {T}$
is a tilting subcategory of
![]() $\mathscr {A}$
, for every object
$\mathscr {A}$
, for every object
![]() $A\in \mathscr {A}$
, there is a short exact sequence
$A\in \mathscr {A}$
, there is a short exact sequence
where
![]() $X_A\in {\mathrm {Fac}}(\mathscr {T})$
and
$X_A\in {\mathrm {Fac}}(\mathscr {T})$
and
![]() $Y_A\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
. Next, we construct the second short exact sequence in the definition of the cotorsion pair. Let
$Y_A\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
. Next, we construct the second short exact sequence in the definition of the cotorsion pair. Let
![]() $A\in \mathscr {A}$
and let
$A\in \mathscr {A}$
and let
![]() $0\longrightarrow K\longrightarrow P\longrightarrow A\longrightarrow 0$
be a short exact sequence in
$0\longrightarrow K\longrightarrow P\longrightarrow A\longrightarrow 0$
be a short exact sequence in
![]() $\mathscr {A}$
, where P is projective. Let
$\mathscr {A}$
, where P is projective. Let
![]() $0\longrightarrow K\longrightarrow X_K\longrightarrow Y_K\longrightarrow 0$
be a short exact sequence such that
$0\longrightarrow K\longrightarrow X_K\longrightarrow Y_K\longrightarrow 0$
be a short exact sequence such that
![]() $X_K\in {\mathrm {Fac}}(\mathscr {T})$
and
$X_K\in {\mathrm {Fac}}(\mathscr {T})$
and
![]() $Y_K\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
. Consider the following pushout diagram:
$Y_K\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
. Consider the following pushout diagram:

Since
![]() $P, Y_K\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
and
$P, Y_K\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
and
![]() ${}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
is closed under extensions, then
${}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
is closed under extensions, then
![]() $U\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
. Hence, the second row in the diagram is the desired short exact sequence. Finally, it is clear that
$U\in {}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}$
. Hence, the second row in the diagram is the desired short exact sequence. Finally, it is clear that
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, {\mathrm {Fac}}(\mathscr {T}))=0$
. So we have verified all of the conditions of a cotorsion pair.
${\mathrm {Ext}}^1_{\mathscr {A}}({}^{\perp _1}{(\mathrm {Fac}(\mathscr {T}))}, {\mathrm {Fac}}(\mathscr {T}))=0$
. So we have verified all of the conditions of a cotorsion pair.
As a corollary of the above theorem, we can recover one of the main results of [Reference Buan and Zhou16]. For this, we need some preparations. Let us begin by recalling the original definition of a support
![]() $\tau $
-tilting module [Reference Adachi, Iyama and Reiten1]. This definition is based on
$\tau $
-tilting module [Reference Adachi, Iyama and Reiten1]. This definition is based on
![]() $\tau : {\mathrm {{mod\mbox {-}}}} \Lambda \to {\mathrm {{mod\mbox {-}}}} \Lambda $
, the Auslander–Reiten translation in
$\tau : {\mathrm {{mod\mbox {-}}}} \Lambda \to {\mathrm {{mod\mbox {-}}}} \Lambda $
, the Auslander–Reiten translation in
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
(see [Reference Assem, Simson and Skowronski4, Chapter IV]).
${\mathrm {{mod\mbox {-}}}} \Lambda $
(see [Reference Assem, Simson and Skowronski4, Chapter IV]).
Definition 5.8 (See [Reference Adachi, Iyama and Reiten1, Definition 0.1])
Let
![]() $\Lambda $
be an Artin algebra. A module T in
$\Lambda $
be an Artin algebra. A module T in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
is called
${\mathrm {{mod\mbox {-}}}}\Lambda $
is called
![]() $\tau $
-rigid if
$\tau $
-rigid if
![]() ${\mathrm {Hom}}_{\Lambda }(T, \tau T)=0$
. It is called
${\mathrm {Hom}}_{\Lambda }(T, \tau T)=0$
. It is called
![]() $\tau $
-tilting if it is
$\tau $
-tilting if it is
![]() $\tau $
-rigid and
$\tau $
-rigid and
![]() $|T|=|\Lambda |$
. A support
$|T|=|\Lambda |$
. A support
![]() $\tau $
-tilting module T in
$\tau $
-tilting module T in
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
is a module T that is a
${\mathrm {{mod\mbox {-}}}} \Lambda $
is a module T that is a
![]() $\tau $
-tilting module in
$\tau $
-tilting module in
![]() ${\mathrm {{mod\mbox {-}}}}(\Lambda /\langle e\rangle )$
, where
${\mathrm {{mod\mbox {-}}}}(\Lambda /\langle e\rangle )$
, where
![]() $\langle e \rangle $
is the ideal generated by some idempotent
$\langle e \rangle $
is the ideal generated by some idempotent
![]() $e \in \Lambda $
.
$e \in \Lambda $
.
As it is mentioned in Remark 3.2, by [Reference Jasso27, Proposition 2.14], T is a support
![]() $\tau $
-tilting module in
$\tau $
-tilting module in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
if and only if
${\mathrm {{mod\mbox {-}}}}\Lambda $
if and only if
![]() ${\mathrm {add}}(T)$
is a support
${\mathrm {add}}(T)$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
. We now show that every support
${\mathrm {{mod\mbox {-}}}}\Lambda $
. We now show that every support
![]() $\tau $
-tilting subcategory in
$\tau $
-tilting subcategory in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
is of the form
${\mathrm {{mod\mbox {-}}}}\Lambda $
is of the form
![]() ${\mathrm {add}}(T)$
for some
${\mathrm {add}}(T)$
for some
![]() $\tau $
-tilting module T in
$\tau $
-tilting module T in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
.
${\mathrm {{mod\mbox {-}}}}\Lambda $
.
Proposition 5.9 Let
![]() $\Lambda $
be an Artin algebra. Then every support
$\Lambda $
be an Artin algebra. Then every support
![]() $\tau $
-tilting subcategory
$\tau $
-tilting subcategory
![]() $\mathscr {T}$
of
$\mathscr {T}$
of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
is of the form
${\mathrm {{mod\mbox {-}}}} \Lambda $
is of the form
![]() ${\mathrm {add}}(T)$
, where T is a support
${\mathrm {add}}(T)$
, where T is a support
![]() $\tau $
-tilting module in
$\tau $
-tilting module in
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
.
${\mathrm {{mod\mbox {-}}}} \Lambda $
.
Proof. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
. By Proposition 3.7, there exists a support
${\mathrm {{mod\mbox {-}}}} \Lambda $
. By Proposition 3.7, there exists a support
![]() $\tau $
-tilting module T such that
$\tau $
-tilting module T such that
![]() ${\mathrm {Fac}}(T)={\mathrm {Fac}}(\mathscr {T})$
. We show that
${\mathrm {Fac}}(T)={\mathrm {Fac}}(\mathscr {T})$
. We show that
![]() ${\mathscr {T}={\mathrm {add}}(T)}$
. First, we note that by the construction of T in Proposition 3.7, we have
${\mathscr {T}={\mathrm {add}}(T)}$
. First, we note that by the construction of T in Proposition 3.7, we have
![]() $T\in \mathscr {T}$
. Therefore,
$T\in \mathscr {T}$
. Therefore,
![]() ${\mathrm {add}}(T)\subseteq \mathscr {T}$
, since T is additively closed subcategory of
${\mathrm {add}}(T)\subseteq \mathscr {T}$
, since T is additively closed subcategory of
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
. Next, let
${\mathrm {{mod\mbox {-}}}}\Lambda $
. Next, let
![]() $X\in \mathscr {T}$
, then
$X\in \mathscr {T}$
, then
![]() $X\in {\mathrm {Fac}}(T)$
. By Proposition 2.5 of [Reference Zhang36], there exists a short exact sequence
$X\in {\mathrm {Fac}}(T)$
. By Proposition 2.5 of [Reference Zhang36], there exists a short exact sequence
where
![]() $T'\in {\mathrm {add}}(T)$
and
$T'\in {\mathrm {add}}(T)$
and
![]() $K' \in {\mathrm {Fac}}(T)$
. Since T is a support
$K' \in {\mathrm {Fac}}(T)$
. Since T is a support
![]() $\tau $
-tilting module, the above short exact sequence splits and hence
$\tau $
-tilting module, the above short exact sequence splits and hence
![]() $X\in {\mathrm {add}}(T)$
. Thus,
$X\in {\mathrm {add}}(T)$
. Thus,
![]() $\mathscr {T}={\mathrm {add}}(T)$
.
$\mathscr {T}={\mathrm {add}}(T)$
.
Corollary 5.10 (See [Reference Buan and Zhou16, Theorem 4.6])
Let
![]() $\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
, where
$\mathscr {A}={\mathrm {{mod\mbox {-}}}}\Lambda $
, where
![]() $\Lambda $
is an Artin algebra. Then there is a bijection between the collection of all support
$\Lambda $
is an Artin algebra. Then there is a bijection between the collection of all support
![]() $\tau $
-tilting modules and the collection of all left weak cotorsion torsion triples.
$\tau $
-tilting modules and the collection of all left weak cotorsion torsion triples.
6 Summary of dual results
In this section, we collect the dual of our results in the previous sections. Given the similarity in their arguments, we list the results without their corresponding proofs. Throughout this section, we assume that
![]() $\mathscr {A}$
is an abelian category with enough injective objects. For a subcategory
$\mathscr {A}$
is an abelian category with enough injective objects. For a subcategory
![]() $\mathscr {U}$
of
$\mathscr {U}$
of
![]() $\mathscr {A}$
, let
$\mathscr {A}$
, let
![]() ${\mathrm {Sub}} \mathscr {U}$
be the full subcategory of
${\mathrm {Sub}} \mathscr {U}$
be the full subcategory of
![]() $\mathscr {A}$
consisting of all subobjects of finite direct sums of objects in
$\mathscr {A}$
consisting of all subobjects of finite direct sums of objects in
![]() $\mathscr {U}$
.
$\mathscr {U}$
.
We start with the definition of a
![]() $\tau ^{-}$
-tilting subcategory of
$\tau ^{-}$
-tilting subcategory of
![]() $\mathscr {A}$
. Recall [Reference Adachi, Iyama and Reiten1, Section. 2.2] that a
$\mathscr {A}$
. Recall [Reference Adachi, Iyama and Reiten1, Section. 2.2] that a
![]() $\Lambda $
-module M, where
$\Lambda $
-module M, where
![]() $\Lambda $
is an Artin algebra, is called
$\Lambda $
is an Artin algebra, is called
![]() $\tau ^{-}$
-tilting if it is
$\tau ^{-}$
-tilting if it is
![]() $\tau ^{-}$
-rigid, i.e.,
$\tau ^{-}$
-rigid, i.e.,
![]() ${\mathrm {Hom}}_{\Lambda }(\tau ^{-}M, M)=0$
, and
${\mathrm {Hom}}_{\Lambda }(\tau ^{-}M, M)=0$
, and
![]() $|M|=|\Lambda |$
. It follows from [Reference Auslander and Smalø6, Proposition 5.6] that M is
$|M|=|\Lambda |$
. It follows from [Reference Auslander and Smalø6, Proposition 5.6] that M is
![]() $\tau ^{-}$
-rigid if and only if
$\tau ^{-}$
-rigid if and only if
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}({\mathrm {Sub}} M,M)=0.$
Here,
${\mathrm {Ext}}^1_{\mathscr {A}}({\mathrm {Sub}} M,M)=0.$
Here,
![]() ${\mathrm {Sub}} M$
means the subcategory of
${\mathrm {Sub}} M$
means the subcategory of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
consisting of all subobjects of
${\mathrm {{mod\mbox {-}}}} \Lambda $
consisting of all subobjects of
![]() ${\mathrm {add}}(M)$
. This motivates the following definition.
${\mathrm {add}}(M)$
. This motivates the following definition.
Definition 6.1 Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough injective objects. Let
![]() $\mathscr {U}$
be an additive full subcategory of
$\mathscr {U}$
be an additive full subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {U}$
is called a weak support
$\mathscr {U}$
is called a weak support
![]() $\tau ^{-}$
-tilting subcategory if:
$\tau ^{-}$
-tilting subcategory if:
-
1.
 ${\mathrm {Ext}}^1_{\mathscr {A}}({\mathrm {Sub}}\mathscr {U},\mathscr {U})=0.$
${\mathrm {Ext}}^1_{\mathscr {A}}({\mathrm {Sub}}\mathscr {U},\mathscr {U})=0.$
-
2. For every injective object I in
 $\mathscr {A}$
, there exists an exact sequence such that
$\mathscr {A}$
, there exists an exact sequence such that $$\begin{align*}0\longrightarrow U^0\longrightarrow U^1\stackrel{g}\longrightarrow I\end{align*}$$
$$\begin{align*}0\longrightarrow U^0\longrightarrow U^1\stackrel{g}\longrightarrow I\end{align*}$$
 $U^0$
and
$U^0$
and
 $U^1$
are in
$U^1$
are in
 $\mathscr {U}$
and g is a right
$\mathscr {U}$
and g is a right
 $\mathscr {U}$
-approximation of I.
$\mathscr {U}$
-approximation of I.
If, furthermore,
![]() $\mathscr {U}$
is a covariantly finite subcategory of
$\mathscr {U}$
is a covariantly finite subcategory of
![]() $\mathscr {A}$
, it is called a support
$\mathscr {A}$
, it is called a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathscr {A}$
. A support
$\mathscr {A}$
. A support
![]() $\tau ^-$
-tilting subcategory
$\tau ^-$
-tilting subcategory
![]() $\mathscr {U}$
of
$\mathscr {U}$
of
![]() $\mathscr {A}$
is called a
$\mathscr {A}$
is called a
![]() $\tau ^-$
-tilting subcategory if the approximation
$\tau ^-$
-tilting subcategory if the approximation
![]() $g: U^1 \longrightarrow I$
is nonzero for every injective object I.
$g: U^1 \longrightarrow I$
is nonzero for every injective object I.
Definition 6.2 Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. A pair of full subcategories
$\mathscr {A}$
be an abelian category with enough injective objects. A pair of full subcategories
![]() $(\mathscr {C}, \mathscr {D})$
of
$(\mathscr {C}, \mathscr {D})$
of
![]() $\mathscr {A}$
is called a
$\mathscr {A}$
is called a
![]() $\tau ^-$
-cotorsion pair if:
$\tau ^-$
-cotorsion pair if:
-
1.
 $\mathscr {D} = \mathscr {C}^{\perp _1}$
.
$\mathscr {D} = \mathscr {C}^{\perp _1}$
. -
2. For every injective object
 $I \in \mathscr {A}$
, there is an exact sequence where
$I \in \mathscr {A}$
, there is an exact sequence where $$\begin{align*}0\longrightarrow D\longrightarrow C\stackrel{g}\longrightarrow I,\end{align*}$$
$$\begin{align*}0\longrightarrow D\longrightarrow C\stackrel{g}\longrightarrow I,\end{align*}$$
 $C \in \mathscr {C}\cap \mathscr {D}$
,
$C \in \mathscr {C}\cap \mathscr {D}$
,
 $D \in \mathscr {D}$
, and g is a right
$D \in \mathscr {D}$
, and g is a right
 $\mathscr {C}$
-approximation.
$\mathscr {C}$
-approximation.
-
3.
 $\mathscr {C}\cap \mathscr {D}$
is a covariantly finite subcategory of
$\mathscr {C}\cap \mathscr {D}$
is a covariantly finite subcategory of
 $\mathscr {A}$
.
$\mathscr {A}$
.
Definition 6.3 A triple
![]() $(\mathscr {T}, \mathscr {F}, \mathscr {D})$
of full subcategories in
$(\mathscr {T}, \mathscr {F}, \mathscr {D})$
of full subcategories in
![]() $\mathscr {A}$
is called a
$\mathscr {A}$
is called a
![]() $\tau ^-$
-torsion cotorsion triple, or simply a
$\tau ^-$
-torsion cotorsion triple, or simply a
![]() $\tau ^-$
-triple, if
$\tau ^-$
-triple, if
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair and
$(\mathscr {T}, \mathscr {F})$
is a torsion pair and
![]() $(\mathscr {F}, \mathscr {D})$
is a
$(\mathscr {F}, \mathscr {D})$
is a
![]() $\tau ^-$
-cotorsion pair.
$\tau ^-$
-cotorsion pair.
A triple
![]() $(\mathscr {T}, \mathscr {F}, \mathscr {D})$
of subcategories of
$(\mathscr {T}, \mathscr {F}, \mathscr {D})$
of subcategories of
![]() $\mathscr {A}$
is called a torsion cotorsion triple if
$\mathscr {A}$
is called a torsion cotorsion triple if
![]() $(\mathscr {T}, \mathscr {F})$
is a torsion pair and
$(\mathscr {T}, \mathscr {F})$
is a torsion pair and
![]() $(\mathscr {F}, \mathscr {D})$
is a cotorsion pair.
$(\mathscr {F}, \mathscr {D})$
is a cotorsion pair.
Proposition 6.4 (Dual of Proposition 4.6)
Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Then every torsion cotorsion pair
$\mathscr {A}$
be an abelian category with enough injective objects. Then every torsion cotorsion pair
![]() $(\mathscr {T}, \mathscr {F}, \mathscr {D})$
in
$(\mathscr {T}, \mathscr {F}, \mathscr {D})$
in
![]() $\mathscr {A}$
is a
$\mathscr {A}$
is a
![]() $\tau ^-$
-triple.
$\tau ^-$
-triple.
Proposition 6.5 (Dual of Proposition 4.7)
Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough injective objects. Let
![]() $(\mathscr {T}, \mathscr {F}, \mathscr {D})$
be a
$(\mathscr {T}, \mathscr {F}, \mathscr {D})$
be a
![]() $\tau ^-$
-triple in
$\tau ^-$
-triple in
![]() $\mathscr {A}$
. Then, for every object
$\mathscr {A}$
. Then, for every object
![]() $A\in \mathscr {A}$
, there exists an exact sequence
$A\in \mathscr {A}$
, there exists an exact sequence
where
![]() $D\in \mathscr {D}$
,
$D\in \mathscr {D}$
,
![]() $F\in \mathscr {F}$
, and g is a right
$F\in \mathscr {F}$
, and g is a right
![]() $\mathscr {F}$
-approximation.
$\mathscr {F}$
-approximation.
Lemma 6.6 (Dual of Lemma 5.6)
Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough injective objects. Let
![]() $(\mathscr {T}, \mathscr {F}, \mathscr {D})$
be a
$(\mathscr {T}, \mathscr {F}, \mathscr {D})$
be a
![]() $\tau ^-$
-triple in
$\tau ^-$
-triple in
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {F}={\mathrm {Sub}}(\mathscr {F}\cap \mathscr {D})$
.
$\mathscr {F}={\mathrm {Sub}}(\mathscr {F}\cap \mathscr {D})$
.
Proposition 6.7 (Dual of Propositions 5.2 and 5.3 and Lemma 5.1)
Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough injective objects. Let
![]() $\mathscr {U}$
be a support
$\mathscr {U}$
be a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
is a
![]() $\tau ^-$
-cotorsion pair and
$\tau ^-$
-cotorsion pair and
is a torsion pair in
![]() $\mathscr {A}$
. Moreover,
$\mathscr {A}$
. Moreover,
Corollary 6.8 (Dual of Corollary 5.4)
Let
![]() $\mathscr {A}$
be an abelian category with enough injectives. Let
$\mathscr {A}$
be an abelian category with enough injectives. Let
![]() $\mathscr {U}$
be a support
$\mathscr {U}$
be a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() ${\mathrm {Sub}}\mathscr {U}$
is a functorially finite torsion-free class of
${\mathrm {Sub}}\mathscr {U}$
is a functorially finite torsion-free class of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Lemma 6.9 (Dual of Lemma 5.5)
Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough injective objects. Let
![]() $(\mathscr {T}, \mathscr {F}, \mathscr {D})$
be a
$(\mathscr {T}, \mathscr {F}, \mathscr {D})$
be a
![]() $\tau ^-$
-triple in
$\tau ^-$
-triple in
![]() $\mathscr {A}$
. Then
$\mathscr {A}$
. Then
![]() $\mathscr {F}\cap \mathscr {D}$
is a support
$\mathscr {F}\cap \mathscr {D}$
is a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Let
![]() $\mathscr {U}$
be an additively closed full subcategory
$\mathscr {U}$
be an additively closed full subcategory
![]() $\mathscr {A}$
. By [Reference Bauer, Botnan, Oppermann and Steen7, Section 2.3],
$\mathscr {A}$
. By [Reference Bauer, Botnan, Oppermann and Steen7, Section 2.3],
![]() $\mathscr {U}$
is called a cotilting subcategory if it satisfies the following conditions.
$\mathscr {U}$
is called a cotilting subcategory if it satisfies the following conditions.
-
(i)
 $\mathscr {U}$
is a covariantly finite subcategory of
$\mathscr {U}$
is a covariantly finite subcategory of
 $\mathscr {A}$
.
$\mathscr {A}$
. -
(ii)
 ${\mathrm {Ext}}^1_{\mathscr {A}}(U_1, U_2)=0$
, for all
${\mathrm {Ext}}^1_{\mathscr {A}}(U_1, U_2)=0$
, for all
 $U_1, U_2 \in \mathscr {U}$
.
$U_1, U_2 \in \mathscr {U}$
. -
(iii) Every object
 $U \in \mathscr {U}$
has injective dimension at most
$U \in \mathscr {U}$
has injective dimension at most
 $1$
.
$1$
. -
(iv) For every injective object I in
 $\mathscr {A}$
, there exists a short exact sequence with
$\mathscr {A}$
, there exists a short exact sequence with $$\begin{align*}0 \longrightarrow U_1 {\longrightarrow} U_0 \longrightarrow I \longrightarrow 0,\end{align*}$$
$$\begin{align*}0 \longrightarrow U_1 {\longrightarrow} U_0 \longrightarrow I \longrightarrow 0,\end{align*}$$
 $U^i \in \mathscr {U}$
.
$U^i \in \mathscr {U}$
.
If
![]() $\mathscr {U}$
only satisfies the conditions
$\mathscr {U}$
only satisfies the conditions
![]() $(ii)$
–
$(ii)$
–
![]() $(iv)$
, it is called a weak cotilting subcategory of
$(iv)$
, it is called a weak cotilting subcategory of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Theorem 6.10 (Dual of Theorem 5.7)
Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Then there is a bijection
$\mathscr {A}$
be an abelian category with enough injective objects. Then there is a bijection
 $$\begin{align*}\lbrace \mbox{support } \tau^{-}\mbox{-tilting subcategories}\rbrace &~~~~\longleftrightarrow~~~~ \lbrace \tau^{-}\mbox{-torsion cotorsion triples}\rbrace\\\mathscr {U}&~~~~\longrightarrow ~~~~~({}^{\perp _0}{\mathscr {U}}, {\mathrm {Sub}}\mathscr {U}, ({\mathrm {Sub}}\mathscr {U})^{\perp _1})\\\mathscr{F}\cap\mathscr{D}&~~\longleftarrow ~~~(\mathscr{T}, \mathscr{F}, \mathscr{D}).\end{align*}$$
$$\begin{align*}\lbrace \mbox{support } \tau^{-}\mbox{-tilting subcategories}\rbrace &~~~~\longleftrightarrow~~~~ \lbrace \tau^{-}\mbox{-torsion cotorsion triples}\rbrace\\\mathscr {U}&~~~~\longrightarrow ~~~~~({}^{\perp _0}{\mathscr {U}}, {\mathrm {Sub}}\mathscr {U}, ({\mathrm {Sub}}\mathscr {U})^{\perp _1})\\\mathscr{F}\cap\mathscr{D}&~~\longleftarrow ~~~(\mathscr{T}, \mathscr{F}, \mathscr{D}).\end{align*}$$
This bijection restricts to a bijection between the collection of all cotilting subcategories of
![]() $\mathscr {A}$
and the collections of all torsion cotorsion triples in
$\mathscr {A}$
and the collections of all torsion cotorsion triples in
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Proposition 6.11 (Dual of Proposition 5.9)
Let
![]() $\Lambda $
be an Artin algebra. Then every support
$\Lambda $
be an Artin algebra. Then every support
![]() $\tau ^{-}$
-tilting subcategory
$\tau ^{-}$
-tilting subcategory
![]() $\mathscr {T}$
of
$\mathscr {T}$
of
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
is of the form
${\mathrm {{mod\mbox {-}}}} \Lambda $
is of the form
![]() ${\mathrm {add}}(T)$
, where T is a support
${\mathrm {add}}(T)$
, where T is a support
![]() $\tau ^{-}$
-tilting module in
$\tau ^{-}$
-tilting module in
![]() ${\mathrm {{mod\mbox {-}}}} \Lambda $
.
${\mathrm {{mod\mbox {-}}}} \Lambda $
.
7 Connection to silting and cosilting modules
This section is divided into two subsections and is devoted to the study of the connections between support
![]() $\tau $
-tilting and support
$\tau $
-tilting and support
![]() $\tau ^{-}$
-tilting subcategories with silting and cosilting theories in
$\tau ^{-}$
-tilting subcategories with silting and cosilting theories in
![]() $\mathrm{Mod}\mbox {-}R$
, respectively, where R is an associative unitary ring. In particular, we characterize all support
$\mathrm{Mod}\mbox {-}R$
, respectively, where R is an associative unitary ring. In particular, we characterize all support
![]() $\tau $
- and support
$\tau $
- and support
![]() $\tau ^-$
-tilting subcategories of
$\tau ^-$
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
.
$\mathrm{Mod}\mbox {-}R$
.
7.1 Silting modules and support
 $\tau $
-tilting subcategories
$\tau $
-tilting subcategories
Our aim in this subsection is to characterize all support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-} R$
. We do this by providing a bijection between the equivalence classes of all support
$\mathrm{Mod}\mbox {-} R$
. We do this by providing a bijection between the equivalence classes of all support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
and the collection of all equivalent classes of the certain R-modules, the so-called finendo quasitilting R-modules. It is known that all silting modules are finendo quasitilting. As a result, it will be shown that
$\mathrm{Mod}\mbox {-}R$
and the collection of all equivalent classes of the certain R-modules, the so-called finendo quasitilting R-modules. It is known that all silting modules are finendo quasitilting. As a result, it will be shown that
![]() ${\mathrm {Add}}(S)$
is a
${\mathrm {Add}}(S)$
is a
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
, where S is a silting R-module.
$\mathrm{Mod}\mbox {-}R$
, where S is a silting R-module.
For a module M in
![]() $\mathrm{Mod}\mbox {-}R$
, let
$\mathrm{Mod}\mbox {-}R$
, let
![]() ${\mathrm {Add}}(M)$
denote the class of all modules isomorphic to a direct summand of an arbitrary direct sum of copies of M. We also let
${\mathrm {Add}}(M)$
denote the class of all modules isomorphic to a direct summand of an arbitrary direct sum of copies of M. We also let
![]() ${\mathrm {Gen}}(M)$
be the subcategory of
${\mathrm {Gen}}(M)$
be the subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
consisting of all M-generated modules, i.e., all modules isomorphic to epimorphic images of modules in
$\mathrm{Mod}\mbox {-}R$
consisting of all M-generated modules, i.e., all modules isomorphic to epimorphic images of modules in
![]() ${\mathrm {Add}}(M)$
. Moreover, we let
${\mathrm {Add}}(M)$
. Moreover, we let
![]() $\mathrm {Pres}(M)$
be the subcategory of
$\mathrm {Pres}(M)$
be the subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
consisting of all M-presented modules, i.e., all modules that admit an
$\mathrm{Mod}\mbox {-}R$
consisting of all M-presented modules, i.e., all modules that admit an
![]() ${\mathrm {Add}}(M)$
-presentation. Recall that an
${\mathrm {Add}}(M)$
-presentation. Recall that an
![]() ${\mathrm {Add}}(M)$
-presentation of an R-module X is an exact sequence
${\mathrm {Add}}(M)$
-presentation of an R-module X is an exact sequence
with
![]() $M_1$
and
$M_1$
and
![]() $M_0$
in
$M_0$
in
![]() ${\mathrm {Add}}(M)$
.
${\mathrm {Add}}(M)$
.
Let
![]() $\sigma $
be a morphism in
$\sigma $
be a morphism in
![]() ${\mathrm {Prj}}(R) $
. Let
${\mathrm {Prj}}(R) $
. Let
![]() $\mathscr {D}_{\sigma }$
be the class of all modules M in
$\mathscr {D}_{\sigma }$
be the class of all modules M in
![]() $\mathrm{Mod}\mbox {-}R$
such that the induced homomorphism
$\mathrm{Mod}\mbox {-}R$
such that the induced homomorphism
![]() ${\mathrm {Hom}}_R(\sigma , M)$
is surjective.
${\mathrm {Hom}}_R(\sigma , M)$
is surjective.
Definition 7.1.1 (See[Reference Angeleri Hügel, Marks and Vitória2, Definition 3.7])
An R-module S is called a partial silting module if there exists a projective presentation
![]() $\sigma $
of S such that
$\sigma $
of S such that
![]() $\mathscr {D}_{\sigma }$
contains S and is a torsion class in
$\mathscr {D}_{\sigma }$
contains S and is a torsion class in
![]() $\mathrm{Mod}\mbox {-}R$
. S is called a silting module if there is a projective presentation
$\mathrm{Mod}\mbox {-}R$
. S is called a silting module if there is a projective presentation
![]() $\sigma $
of S such that
$\sigma $
of S such that
![]() ${\mathrm {Gen}}(S)=\mathscr {D}_{\sigma }.$
${\mathrm {Gen}}(S)=\mathscr {D}_{\sigma }.$
Remark 7.1.2 By [Reference Angeleri Hügel, Marks and Vitória2, Remark 3.8], every silting module is a partial silting module; hence,
![]() ${\mathrm {Gen}}(S)$
is a torsion class. Support
${\mathrm {Gen}}(S)$
is a torsion class. Support
![]() $\tau $
-tilting modules over a finite-dimensional k-algebra are examples of silting modules (see [Reference Angeleri Hügel, Marks and Vitória2, Proposition 3.15]).
$\tau $
-tilting modules over a finite-dimensional k-algebra are examples of silting modules (see [Reference Angeleri Hügel, Marks and Vitória2, Proposition 3.15]).
Definition 7.1.3 (See [Reference Angeleri Hügel, Marks and Vitória2, Lemdef 3.1])
An R-module T is called quasitilting if
![]() $\mathrm {Pres}(T)={\mathrm {Gen}}(T)$
and T is Ext-projective in
$\mathrm {Pres}(T)={\mathrm {Gen}}(T)$
and T is Ext-projective in
![]() ${\mathrm {Gen}}(T)$
.
${\mathrm {Gen}}(T)$
.
Recall that an R-module T is Ext-projective with respect to a subcategory
![]() $\mathscr {X}$
of
$\mathscr {X}$
of
![]() $\mathrm{Mod}\mbox {-}R$
, if
$\mathrm{Mod}\mbox {-}R$
, if
![]() $T \in \mathscr {X}$
and
$T \in \mathscr {X}$
and
![]() ${\mathrm {Ext}}^1_R(T, \mathscr {X})=0$
.
${\mathrm {Ext}}^1_R(T, \mathscr {X})=0$
.
The following proposition collects some basic properties of quasitilting modules. Their proofs can be found in [Reference Angeleri Hügel, Marks and Vitória2, Lemdef 3.1, Lemma 3.3, and Proposition 3.2]. Recall that an R-modules T is called finendo if it is finitely generated over its endomorphism ring.
Proposition 7.1.4 Let T be a quasitilting R-module. Then the following statements hold.
-
1. If
 $X\in {\mathrm {Gen}}(T)$
then, there exist a set J and a short exact sequence such that
$X\in {\mathrm {Gen}}(T)$
then, there exist a set J and a short exact sequence such that $$\begin{align*}0\longrightarrow{\mathrm{Ker}}\pi\longrightarrow T^{(J)}\stackrel{\pi}\longrightarrow X\longrightarrow 0\end{align*}$$
$$\begin{align*}0\longrightarrow{\mathrm{Ker}}\pi\longrightarrow T^{(J)}\stackrel{\pi}\longrightarrow X\longrightarrow 0\end{align*}$$
 ${\mathrm {Ker}}\pi \in {\mathrm {Gen}}(T)$
and
${\mathrm {Ker}}\pi \in {\mathrm {Gen}}(T)$
and
 $T^{(J)}$
is the coproduct of copies of T indexed by J. That is,
$T^{(J)}$
is the coproduct of copies of T indexed by J. That is,
 ${\mathrm {Gen}}(T)$
is closed with respect to the kernels of epimorphisms.
${\mathrm {Gen}}(T)$
is closed with respect to the kernels of epimorphisms.
-
2.
 ${\mathrm {Add}}(T)$
is the class of
${\mathrm {Add}}(T)$
is the class of
 ${\mathrm {Ext}}$
-projective modules in
${\mathrm {Ext}}$
-projective modules in
 ${\mathrm {Gen}}(T)$
.
${\mathrm {Gen}}(T)$
. -
3. The following are equivalent.
-
(i) T is a finendo quasitilting R-module.
-
(ii)
 ${\mathrm {Gen}}(T)$
is a torsion class and T is a tilting
${\mathrm {Gen}}(T)$
is a torsion class and T is a tilting
 $R/{\mathrm {ann}}(R)$
-module.
$R/{\mathrm {ann}}(R)$
-module. -
(iii) T is an
 ${\mathrm {Ext}}$
-projective module in
${\mathrm {Ext}}$
-projective module in
 ${\mathrm {Gen}}(T)$
and there exists an exact sequence such that
${\mathrm {Gen}}(T)$
and there exists an exact sequence such that $$\begin{align*}R\stackrel{f}\longrightarrow T_0\longrightarrow T_1\longrightarrow 0\end{align*}$$
$$\begin{align*}R\stackrel{f}\longrightarrow T_0\longrightarrow T_1\longrightarrow 0\end{align*}$$
 $T_0, T_1\in {\mathrm {Add}}(T)$
and f is a left
$T_0, T_1\in {\mathrm {Add}}(T)$
and f is a left
 ${\mathrm {Gen}}(T)$
-approximation.
${\mathrm {Gen}}(T)$
-approximation.
-
Proposition 7.1.5 Let T be a finendo quasitilting module in
![]() $\mathrm{Mod}\mbox {-}R$
. Then
$\mathrm{Mod}\mbox {-}R$
. Then
![]() ${\mathrm {Add}}(T)$
is a support
${\mathrm {Add}}(T)$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
.
$\mathrm{Mod}\mbox {-}R$
.
Proof. We show the validity of conditions of Definition 3.1. Note that
![]() ${\mathrm {Fac}}({\mathrm {Add}}(T))={\mathrm {Gen}}(T)$
. Then
${\mathrm {Fac}}({\mathrm {Add}}(T))={\mathrm {Gen}}(T)$
. Then
![]() ${\mathrm {Ext}}^1_R({\mathrm {Add}}(T), {\mathrm {Fac}}({\mathrm {Add}}(T)))=0$
follows from Proposition 7.1.4.2.
${\mathrm {Ext}}^1_R({\mathrm {Add}}(T), {\mathrm {Fac}}({\mathrm {Add}}(T)))=0$
follows from Proposition 7.1.4.2.
By Proposition 7.1.4.3, there exists an exact sequence
where
![]() $T_0, T_1\in {\mathrm {Add}}(T)$
and f is a left
$T_0, T_1\in {\mathrm {Add}}(T)$
and f is a left
![]() ${\mathrm {Gen}}(T)$
-approximation. Since
${\mathrm {Gen}}(T)$
-approximation. Since
![]() $T_0 \in {\mathrm {Add}}(T)$
, f is also a left
$T_0 \in {\mathrm {Add}}(T)$
, f is also a left
![]() ${\mathrm {Add}}(T)$
-approximation. Now let P be a projective R-module. There exists a set J and an epimorphism
${\mathrm {Add}}(T)$
-approximation. Now let P be a projective R-module. There exists a set J and an epimorphism
![]() $R^{(J)}\longrightarrow P\longrightarrow 0$
which is split. Consider the pushout diagram
$R^{(J)}\longrightarrow P\longrightarrow 0$
which is split. Consider the pushout diagram

Since h is a split epimorphism, we get
![]() $\tilde {T}\in {\mathrm {Add}}(T)$
. Also, it follows easily from the universal property of the pushout diagrams that g is a left
$\tilde {T}\in {\mathrm {Add}}(T)$
. Also, it follows easily from the universal property of the pushout diagrams that g is a left
![]() ${\mathrm {Add}}(T)$
-approximation of P.
${\mathrm {Add}}(T)$
-approximation of P.
To complete the proof, we just need to show that
![]() ${\mathrm {Add}}(T)$
is a contravariantly finite subcategory of
${\mathrm {Add}}(T)$
is a contravariantly finite subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. Let
$\mathrm{Mod}\mbox {-}R$
. Let
![]() $M\in \mathrm{Mod}\mbox {-}R$
. Since, by Proposition 7.1.4.3,
$M\in \mathrm{Mod}\mbox {-}R$
. Since, by Proposition 7.1.4.3,
![]() ${\mathrm {Gen}}(T)$
is a torsion class, it is a contravariantly finite subcategory of
${\mathrm {Gen}}(T)$
is a torsion class, it is a contravariantly finite subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. Therefore, there is a monomorphism
$\mathrm{Mod}\mbox {-}R$
. Therefore, there is a monomorphism
![]() $0\longrightarrow X\stackrel {\imath }\longrightarrow M $
such that
$0\longrightarrow X\stackrel {\imath }\longrightarrow M $
such that
![]() $X\in {\mathrm {Gen}}(T)$
. By Proposition 7.1.4.1, there exist a set J and a short exact sequence
$X\in {\mathrm {Gen}}(T)$
. By Proposition 7.1.4.1, there exist a set J and a short exact sequence
such that
![]() ${\mathrm {Ker}} \pi \in {\mathrm {Gen}}(T)$
. We show that
${\mathrm {Ker}} \pi \in {\mathrm {Gen}}(T)$
. We show that
![]() $T^{(J)}\stackrel {\imath \pi }\longrightarrow M$
is a right
$T^{(J)}\stackrel {\imath \pi }\longrightarrow M$
is a right
![]() ${\mathrm {Add}}(T)$
-approximation. To do this, let
${\mathrm {Add}}(T)$
-approximation. To do this, let
![]() $T'\in {\mathrm {Add}}(T)$
and
$T'\in {\mathrm {Add}}(T)$
and
![]() $T'\stackrel {\ell }\longrightarrow M$
be a morphism. Since
$T'\stackrel {\ell }\longrightarrow M$
be a morphism. Since
![]() $\imath $
is a right
$\imath $
is a right
![]() ${\mathrm {Gen}}(T)$
-approximation, there is a morphism
${\mathrm {Gen}}(T)$
-approximation, there is a morphism
![]() $T'\stackrel {\jmath }\longrightarrow X$
such that
$T'\stackrel {\jmath }\longrightarrow X$
such that
![]() $\imath \jmath =\ell $
. By applying
$\imath \jmath =\ell $
. By applying
![]() ${\mathrm {Hom}}_R(T', -)$
on the above short exact sequence and using the fact that
${\mathrm {Hom}}_R(T', -)$
on the above short exact sequence and using the fact that
![]() ${\mathrm {Ker}}\pi \in {\mathrm {Gen}}(T)$
, we conclude that
${\mathrm {Ker}}\pi \in {\mathrm {Gen}}(T)$
, we conclude that
![]() $\jmath $
factors through
$\jmath $
factors through
![]() $\pi $
. Hence,
$\pi $
. Hence,
![]() $\ell $
factors through
$\ell $
factors through
![]() $\imath \pi $
and the result follows.
$\imath \pi $
and the result follows.
As a direct consequence of the above proposition, we have the following.
Corollary 7.1.6 Let S be a silting module in
![]() $\mathrm{Mod}\mbox {-}R$
. Then
$\mathrm{Mod}\mbox {-}R$
. Then
![]() ${\mathrm {Add}}(S)$
is a support
${\mathrm {Add}}(S)$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
.
$\mathrm{Mod}\mbox {-}R$
.
Proof. By [Reference Angeleri Hügel, Marks and Vitória2, Proposition 3.10], every silting R-module is a finendo quasitilting R-module. Now, by the above proposition, the result follows.
We also have a kind of converse to the previous proposition.
Proposition 7.1.7 Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
such that
$\mathrm{Mod}\mbox {-}R$
such that
![]() ${\mathscr {T}={\mathrm {Add}}(T)}$
, for some R-module T. Then T is a finendo quasitilting R-module.
${\mathscr {T}={\mathrm {Add}}(T)}$
, for some R-module T. Then T is a finendo quasitilting R-module.
Proof. Since
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory, there exists a short exact sequence
$\tau $
-tilting subcategory, there exists a short exact sequence
where
![]() $T^0, T^1\in \mathscr {T}$
and f is a left
$T^0, T^1\in \mathscr {T}$
and f is a left
![]() $\mathscr {T}$
-approximation. We note that f also is a left
$\mathscr {T}$
-approximation. We note that f also is a left
![]() ${\mathrm {Fac}}(\mathscr {T})$
-approximation (see, for instance, the proof of Proposition 5.2). On the other hand, since
${\mathrm {Fac}}(\mathscr {T})$
-approximation (see, for instance, the proof of Proposition 5.2). On the other hand, since
![]() ${\mathrm {Fac}}(\mathscr {T})={\mathrm {Fac}}({\mathrm {Add}}(T))={\mathrm {Gen}}(T)$
and
${\mathrm {Fac}}(\mathscr {T})={\mathrm {Fac}}({\mathrm {Add}}(T))={\mathrm {Gen}}(T)$
and
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory, T is Ext-projective in
$\tau $
-tilting subcategory, T is Ext-projective in
![]() ${\mathrm {Gen}}(T)$
. Now Proposition 7.1.4.3 implies that T is a finendo quasitilting module.
${\mathrm {Gen}}(T)$
. Now Proposition 7.1.4.3 implies that T is a finendo quasitilting module.
Let R be a right perfect ring. In this case, it is known that every functorially finite torsion class is generated by a silting module that is constructed by taking an approximation of the ring and then its cokernel [Reference Buan and Zhou16, Theorem 2.4]. In the following, we use a similar idea to provide a version of Proposition 3.7 in
![]() $\mathrm{Mod}\mbox {-}R$
.
$\mathrm{Mod}\mbox {-}R$
.
Proposition 7.1.8 Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. Then there exists a finendo quasitilting module T such that
$\mathrm{Mod}\mbox {-}R$
. Then there exists a finendo quasitilting module T such that
![]() ${\mathrm {Fac}}(\mathscr {T})={\mathrm {Gen}}(T)$
.
${\mathrm {Fac}}(\mathscr {T})={\mathrm {Gen}}(T)$
.
Proof. By Theorem 5.7,
![]() $({}^{\perp _1}{\mathrm {Fac}}(\mathscr {T}), {\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a
$({}^{\perp _1}{\mathrm {Fac}}(\mathscr {T}), {\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is a
![]() $\tau $
-triple. Hence, by Proposition 4.7, for every
$\tau $
-triple. Hence, by Proposition 4.7, for every
![]() $M\in \mathrm{Mod}\mbox {-}R$
, there exists an exact sequence
$M\in \mathrm{Mod}\mbox {-}R$
, there exists an exact sequence
such that
![]() $\phi $
is a left
$\phi $
is a left
![]() ${\mathrm {Fac}}(\mathscr {T})$
-approximation and
${\mathrm {Fac}}(\mathscr {T})$
-approximation and
![]() $C\in {}^{\perp _1}{\mathrm {Fac}}(\mathscr {T})$
, that is, C is an Ext-projective in
$C\in {}^{\perp _1}{\mathrm {Fac}}(\mathscr {T})$
, that is, C is an Ext-projective in
![]() ${\mathrm {Fac}}(\mathscr {T})$
. Hence, by [Reference Angeleri Hügel, Marks and Vitória2, Theorem 3.4], we deduce that there exists a finendo quasitilting R-module T such that
${\mathrm {Fac}}(\mathscr {T})$
. Hence, by [Reference Angeleri Hügel, Marks and Vitória2, Theorem 3.4], we deduce that there exists a finendo quasitilting R-module T such that
![]() ${\mathrm {Fac}}(\mathscr {T})={\mathrm {Gen}}(T)$
.
${\mathrm {Fac}}(\mathscr {T})={\mathrm {Gen}}(T)$
.
Definition 7.1.9 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects. Let
$\mathscr {A}$
be an abelian category with enough projective objects. Let
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
![]() $\mathscr {T}'$
be two support
$\mathscr {T}'$
be two support
![]() $\tau $
-titling subcategories of
$\tau $
-titling subcategories of
![]() $\mathscr {A}$
. We say that
$\mathscr {A}$
. We say that
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
![]() $\mathscr {T}'$
are equivalent if
$\mathscr {T}'$
are equivalent if
![]() ${\mathrm {Fac}}(\mathscr {T})={\mathrm {Fac}}(\mathscr {T}')$
.
${\mathrm {Fac}}(\mathscr {T})={\mathrm {Fac}}(\mathscr {T}')$
.
We now have enough ingredients for the proof of our main theorem. Recall that, by [Reference Angeleri Hügel, Marks and Vitória2, p. 12], two quasitilting modules
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are equivalent if
$T_2$
are equivalent if
![]() ${\mathrm {Add}}(T_1)={\mathrm {Add}}(T_2)$
.
${\mathrm {Add}}(T_1)={\mathrm {Add}}(T_2)$
.
Theorem 7.1.10 There is a bijection between the equivalence classes of support
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
and the equivalence classes of finendo quasitilting R-modules.
$\mathrm{Mod}\mbox {-}R$
and the equivalence classes of finendo quasitilting R-modules.
7.2 Cosilting modules and support
 $\tau ^-$
-tilting subcategories
$\tau ^-$
-tilting subcategories
Our aim in this subsection is to characterize all support
![]() $\tau ^{-}$
-tilting subcategories of
$\tau ^{-}$
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
in terms of cosilting R-modules. Note that cosilting modules coincide with quasicotilting modules coincide (see [Reference Zhang and Wei34, Theorem 4.18]). We show that
$\mathrm{Mod}\mbox {-}R$
in terms of cosilting R-modules. Note that cosilting modules coincide with quasicotilting modules coincide (see [Reference Zhang and Wei34, Theorem 4.18]). We show that
![]() ${\mathrm {Prod}}(T)$
is a
${\mathrm {Prod}}(T)$
is a
![]() $\tau ^{-}$
-tilting subcategory of
$\tau ^{-}$
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
, where T is a quasicotilting R-module, where
$\mathrm{Mod}\mbox {-}R$
, where T is a quasicotilting R-module, where
![]() ${\mathrm {Prod}}(M)$
denotes the class of all modules isomorphic to an arbitrary direct product of copies of M.
${\mathrm {Prod}}(M)$
denotes the class of all modules isomorphic to an arbitrary direct product of copies of M.
For a module M in
![]() $\mathrm{Mod}\mbox {-}R$
, let
$\mathrm{Mod}\mbox {-}R$
, let
![]() ${\mathrm {Cogen}}(M)$
be the subcategory of
${\mathrm {Cogen}}(M)$
be the subcategory of
![]() $\mathrm{Mod}\mbox {-} R$
consisting of all M-cogenerated modules, i.e., all modules isomorphic to a submodule of modules in
$\mathrm{Mod}\mbox {-} R$
consisting of all M-cogenerated modules, i.e., all modules isomorphic to a submodule of modules in
![]() ${\mathrm {Prod}}(M)$
and let
${\mathrm {Prod}}(M)$
and let
![]() $\mathrm {Copres}(M)$
be the subcategory of
$\mathrm {Copres}(M)$
be the subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
consisting of all M-copresented modules, i.e., all modules that admit a
$\mathrm{Mod}\mbox {-}R$
consisting of all M-copresented modules, i.e., all modules that admit a
![]() ${\mathrm {Prod}}(M)$
-copresentation. Recall that a
${\mathrm {Prod}}(M)$
-copresentation. Recall that a
![]() ${\mathrm {Prod}}(M)$
-copresentation of an R-module X is an exact sequence
${\mathrm {Prod}}(M)$
-copresentation of an R-module X is an exact sequence
with
![]() $M_0$
and
$M_0$
and
![]() $M_1$
in
$M_1$
in
![]() ${\mathrm {Prod}}(M)$
.
${\mathrm {Prod}}(M)$
.
Let
![]() $\zeta $
be a morphism in
$\zeta $
be a morphism in
![]() ${\mathrm {Inj}}(R)$
. Let
${\mathrm {Inj}}(R)$
. Let
![]() $\mathscr {B}_{\zeta }$
denote the class of all modules M in
$\mathscr {B}_{\zeta }$
denote the class of all modules M in
![]() $\mathrm{Mod}\mbox {-}R$
such that the induced homomorphism
$\mathrm{Mod}\mbox {-}R$
such that the induced homomorphism
![]() ${\mathrm {Hom}}_R(M, \zeta )$
is surjective.
${\mathrm {Hom}}_R(M, \zeta )$
is surjective.
Definition 7.2.1 (See [Reference Breaz and Pop14, Definition 3.1])
An R-module C is called a partial cosilting module if there is an injective copresentation
![]() $\zeta $
of C such that
$\zeta $
of C such that
![]() $\mathscr {B}_{\zeta }$
contains C and the class
$\mathscr {B}_{\zeta }$
contains C and the class
![]() $\mathscr {B}_\zeta $
is closed under direct products. Moreover, C is called a cosilting module if there is an injective copresentation
$\mathscr {B}_\zeta $
is closed under direct products. Moreover, C is called a cosilting module if there is an injective copresentation
![]() $\zeta $
of C such that
$\zeta $
of C such that
![]() ${\mathrm {Cogen}}(C)=\mathscr {B}_{\zeta }.$
${\mathrm {Cogen}}(C)=\mathscr {B}_{\zeta }.$
By [Reference Breaz and Pop14, Remark 3.2], every cosilting module is a partial cosilting module. In particular, for every cosilting module C,
![]() ${\mathrm {Cogen}}(C)$
is a torsion-free class.
${\mathrm {Cogen}}(C)$
is a torsion-free class.
Definition 7.2.2 (See [Reference Zhang and Wei34, Definition 3.1])
An R-module T is called a quasicotilting module if
![]() ${\mathrm {Cogen}}(T)=\mathrm {Copres}(T)$
and T is
${\mathrm {Cogen}}(T)=\mathrm {Copres}(T)$
and T is
![]() ${\mathrm {Ext}}$
-injective in
${\mathrm {Ext}}$
-injective in
![]() ${\mathrm {Cogen}}(T)$
.
${\mathrm {Cogen}}(T)$
.
Recall that an R-module T is Ext-injective with respect to a subcategory
![]() $\mathscr {X}$
of
$\mathscr {X}$
of
![]() $\mathrm{Mod}\mbox {-}R$
, if
$\mathrm{Mod}\mbox {-}R$
, if
![]() $T \in \mathscr {X}$
and
$T \in \mathscr {X}$
and
![]() ${\mathrm {Ext}}^1_R(\mathscr {X}, T)=0$
.
${\mathrm {Ext}}^1_R(\mathscr {X}, T)=0$
.
By [Reference Zhang and Wei34, Theorem 4.18], quasicotilting modules and cosilting modules coincide, so if T is a quasicotilting R-module, then
![]() ${\mathrm {Cogen}}(T)$
is a torsion-free class. Also, [Reference Zhang and Wei34, Proposition 3.2.2] implies that all quasicotilting R-modules are cofinendo. Recall that R-module T is cofinendo if and only if there exists a right
${\mathrm {Cogen}}(T)$
is a torsion-free class. Also, [Reference Zhang and Wei34, Proposition 3.2.2] implies that all quasicotilting R-modules are cofinendo. Recall that R-module T is cofinendo if and only if there exists a right
![]() ${\mathrm {Prod}}(T)$
-approximation of an injective cogenerator
${\mathrm {Prod}}(T)$
-approximation of an injective cogenerator
![]() $\mathrm{Mod}\mbox {-}R$
(see [Reference Angeleri Hügel, Tonolo and Trlifaj3, Proposition 1.6]).
$\mathrm{Mod}\mbox {-}R$
(see [Reference Angeleri Hügel, Tonolo and Trlifaj3, Proposition 1.6]).
The following proposition collects some of the basic properties of the quasicotilting modules. The proofs can be found in [Reference Zhang and Wei35, Lemma 3.1 and Theorem 3.2].
Proposition 7.2.3 Let E be an injective cogenerator of
![]() $\mathrm{Mod}\mbox {-}R$
. Let T be a quasicoilting R-module. Then the following statements hold.
$\mathrm{Mod}\mbox {-}R$
. Let T be a quasicoilting R-module. Then the following statements hold.
-
1. If
 $X\in {\mathrm {Cogen}}(T)$
, then there exist a set J and a short exact sequence such that
$X\in {\mathrm {Cogen}}(T)$
, then there exist a set J and a short exact sequence such that $$\begin{align*}0\longrightarrow X\stackrel{\imath}\longrightarrow T^J\longrightarrow {\mathrm{Coker}}\imath\longrightarrow 0\end{align*}$$
$$\begin{align*}0\longrightarrow X\stackrel{\imath}\longrightarrow T^J\longrightarrow {\mathrm{Coker}}\imath\longrightarrow 0\end{align*}$$
 ${\mathrm {Coker}}\imath \in {\mathrm {Cogen}}(T)$
and
${\mathrm {Coker}}\imath \in {\mathrm {Cogen}}(T)$
and
 $T^J$
is the product of copies of T indexed by J. That is,
$T^J$
is the product of copies of T indexed by J. That is,
 ${\mathrm {Cogen}}(T)$
is closed with respect to the cokernels of monomorphisms.
${\mathrm {Cogen}}(T)$
is closed with respect to the cokernels of monomorphisms.
-
2.
 ${\mathrm {Prod}}(T)$
is the class of
${\mathrm {Prod}}(T)$
is the class of
 ${\mathrm {Ext}}$
-injective modules in
${\mathrm {Ext}}$
-injective modules in
 ${\mathrm {Cogen}}(T)$
.
${\mathrm {Cogen}}(T)$
. -
3. T is quasicotilting if and only if T is an
 $Ext$
-injective in
$Ext$
-injective in
 ${\mathrm {Cogen}}(T)$
and there exists an exact sequence such that
${\mathrm {Cogen}}(T)$
and there exists an exact sequence such that $$\begin{align*}0\longrightarrow T_0\longrightarrow T_1\stackrel{f}\longrightarrow E \end{align*}$$
$$\begin{align*}0\longrightarrow T_0\longrightarrow T_1\stackrel{f}\longrightarrow E \end{align*}$$
 $T_0, T_1\in {\mathrm {Prod}}(T)$
and f is a right
$T_0, T_1\in {\mathrm {Prod}}(T)$
and f is a right
 ${\mathrm {Cogen}}(T)$
-approximation.
${\mathrm {Cogen}}(T)$
-approximation.
In the following, we show that every quasicotilting module induces a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. The proof is essentially dual to that of Proposition 7.1.5, but we include it for the sake of completeness.
$\mathrm{Mod}\mbox {-}R$
. The proof is essentially dual to that of Proposition 7.1.5, but we include it for the sake of completeness.
Proposition 7.2.4 Let E be an injective cogenerator of
![]() $\mathrm{Mod}\mbox {-}R$
. Let T be a quasicotilting R-module. Then
$\mathrm{Mod}\mbox {-}R$
. Let T be a quasicotilting R-module. Then
![]() ${\mathrm {Prod}}(T)$
is a support
${\mathrm {Prod}}(T)$
is a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
.
$\mathrm{Mod}\mbox {-}R$
.
Proof. We show the validity of the conditions of Definition 6.1. For the first condition, note that
![]() ${\mathrm {Sub}}{\mathrm {Prod}}(T)={\mathrm {Cogen}}(T)$
. The fact that
${\mathrm {Sub}}{\mathrm {Prod}}(T)={\mathrm {Cogen}}(T)$
. The fact that
follows from Proposition 7.2.3(2). For the second condition, consider the exact sequence
of Proposition 7.2.3(3), in which
![]() $T_0, T_1\in {\mathrm {Prod}}(T)$
and f is a right
$T_0, T_1\in {\mathrm {Prod}}(T)$
and f is a right
![]() ${\mathrm {Cogen}}(T)$
-approximation of E. Now let I be an injective R-module. There exists a set J and a monomorphism
${\mathrm {Cogen}}(T)$
-approximation of E. Now let I be an injective R-module. There exists a set J and a monomorphism
![]() $0\longrightarrow I\longrightarrow E^{J}$
which is a split morphism. Consider the pullback diagram
$0\longrightarrow I\longrightarrow E^{J}$
which is a split morphism. Consider the pullback diagram

Since h is a split monomorphism, we get
![]() $\tilde {T}\in {\mathrm {Prod}}(T)$
. Moreover, it follows easily from the universal property of the pullback diagrams that g is a right
$\tilde {T}\in {\mathrm {Prod}}(T)$
. Moreover, it follows easily from the universal property of the pullback diagrams that g is a right
![]() ${\mathrm {Prod}}(T)$
-approximation of I.
${\mathrm {Prod}}(T)$
-approximation of I.
To complete the proof, it remains to show that
![]() ${\mathrm {Prod}}(T)$
is a covariantly finite subcategory of
${\mathrm {Prod}}(T)$
is a covariantly finite subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. Let
$\mathrm{Mod}\mbox {-}R$
. Let
![]() $M\in \mathrm{Mod}\mbox {-}R$
. Since
$M\in \mathrm{Mod}\mbox {-}R$
. Since
![]() ${\mathrm {Cogen}}(T)$
is a torsion-free class, it is a covariantly finite subcategory of
${\mathrm {Cogen}}(T)$
is a torsion-free class, it is a covariantly finite subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. Therefore, there is an epimorphism
$\mathrm{Mod}\mbox {-}R$
. Therefore, there is an epimorphism
![]() $ M\stackrel {\pi }\longrightarrow X\longrightarrow 0$
such that
$ M\stackrel {\pi }\longrightarrow X\longrightarrow 0$
such that
![]() $X\in {\mathrm {Cogen}}(T)$
. By Proposition 7.2.3(1), there exist a set J and a short exact sequence
$X\in {\mathrm {Cogen}}(T)$
. By Proposition 7.2.3(1), there exist a set J and a short exact sequence
such that
![]() ${\mathrm {Coker}} \imath \in {\mathrm {Cogen}}(T)$
. We claim that
${\mathrm {Coker}} \imath \in {\mathrm {Cogen}}(T)$
. We claim that
![]() $M \stackrel {\imath \pi }\longrightarrow T^{J}$
is a left
$M \stackrel {\imath \pi }\longrightarrow T^{J}$
is a left
![]() ${\mathrm {Prod}}(T)$
-approximation. Indeed, let
${\mathrm {Prod}}(T)$
-approximation. Indeed, let
![]() $f: M \longrightarrow \tilde {T}$
be a map with
$f: M \longrightarrow \tilde {T}$
be a map with
![]() $\tilde {T} \in {\mathrm {Prod}}(T)$
. Then f factors through X because
$\tilde {T} \in {\mathrm {Prod}}(T)$
. Then f factors through X because
![]() $\tilde {T} \in {\mathrm {Cogen}}(T)$
. Moreover,
$\tilde {T} \in {\mathrm {Cogen}}(T)$
. Moreover,
![]() ${\mathrm {Cogen}}(T)$
is closed under cokernels of monomorphisms by Proposition 7.2.3(1). Hence, we can lift the factorization f through X using
${\mathrm {Cogen}}(T)$
is closed under cokernels of monomorphisms by Proposition 7.2.3(1). Hence, we can lift the factorization f through X using
![]() $\pi $
and conclude that f factors through
$\pi $
and conclude that f factors through
![]() $\imath \pi $
.
$\imath \pi $
.
The following is a kind of converse to the previous proposition which is also the dual of Proposition 7.1.7.
Proposition 7.2.5 Let E be an injective cogenerator of
![]() $\mathrm{Mod}\mbox {-}R$
. Let
$\mathrm{Mod}\mbox {-}R$
. Let
![]() $\mathscr {U}$
be a support
$\mathscr {U}$
be a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
such that
$\mathrm{Mod}\mbox {-}R$
such that
![]() $\mathscr {U}={\mathrm {Prod}}(T)$
, for some R-module T. Then T is a quasicotilting R-module.
$\mathscr {U}={\mathrm {Prod}}(T)$
, for some R-module T. Then T is a quasicotilting R-module.
Proof. Since
![]() $\mathscr {U}$
is a support
$\mathscr {U}$
is a support
![]() $\tau ^-$
-tilting subcategory, for E there exists an exact sequence
$\tau ^-$
-tilting subcategory, for E there exists an exact sequence
where
![]() $U^0, U^1\in \mathscr {T}$
and f is a right
$U^0, U^1\in \mathscr {T}$
and f is a right
![]() $\mathscr {U}$
-approximation. We note that f is also a right
$\mathscr {U}$
-approximation. We note that f is also a right
![]() ${\mathrm {Sub}}\mathscr {U}$
-approximation. On the other hand, since
${\mathrm {Sub}}\mathscr {U}$
-approximation. On the other hand, since
![]() ${\mathrm {Sub}}\mathscr {U} ={\mathrm {Sub}} {\mathrm {Prod}}(T) ={\mathrm {Cogen}}(T)$
and
${\mathrm {Sub}}\mathscr {U} ={\mathrm {Sub}} {\mathrm {Prod}}(T) ={\mathrm {Cogen}}(T)$
and
![]() $\mathscr {U}$
is a support
$\mathscr {U}$
is a support
![]() $\tau ^-$
-tilting subcategory, T is Ext-injective in
$\tau ^-$
-tilting subcategory, T is Ext-injective in
![]() ${\mathrm {Cogen}}(T)$
. Now Proposition 7.2.3(3) implies that T is a quasicotilting module.
${\mathrm {Cogen}}(T)$
. Now Proposition 7.2.3(3) implies that T is a quasicotilting module.
The following result is a dual of Proposition 7.1.8.
Proposition 7.2.6 Let
![]() $\mathscr {U}$
be a support
$\mathscr {U}$
be a support
![]() $\tau ^-$
-tilting subcategory of
$\tau ^-$
-tilting subcategory of
![]() $\mathrm{Mod}\mbox {-}R$
. Then there exists a quasicotilting module T such that
$\mathrm{Mod}\mbox {-}R$
. Then there exists a quasicotilting module T such that
![]() ${\mathrm {Sub}} \mathscr {U}={\mathrm {Cogen}}(T)$
.
${\mathrm {Sub}} \mathscr {U}={\mathrm {Cogen}}(T)$
.
Proof. By Theorem 6.10,
![]() $({}^{\perp _0}{\mathscr {U}}, {\mathrm {Sub}}\mathscr {U}, ({\mathrm {Sub}}\mathscr {U})^{\perp _1})$
is a
$({}^{\perp _0}{\mathscr {U}}, {\mathrm {Sub}}\mathscr {U}, ({\mathrm {Sub}}\mathscr {U})^{\perp _1})$
is a
![]() $\tau ^-$
-triple. Hence, by Proposition 6.5, for every
$\tau ^-$
-triple. Hence, by Proposition 6.5, for every
![]() $M\in \mathrm{Mod}\mbox {-}R$
, there exists an exact sequence
$M\in \mathrm{Mod}\mbox {-}R$
, there exists an exact sequence
such that
![]() $\phi $
is a right
$\phi $
is a right
![]() ${\mathrm {Sub}} \mathscr {U}$
-approximation and
${\mathrm {Sub}} \mathscr {U}$
-approximation and
![]() $B\in ({\mathrm {Sub}}\mathscr {U})^{\perp _1}$
, that is, B is an
$B\in ({\mathrm {Sub}}\mathscr {U})^{\perp _1}$
, that is, B is an
![]() ${\mathrm {Ext}}$
-injective module in
${\mathrm {Ext}}$
-injective module in
![]() ${\mathrm {Sub}}\mathscr {U}$
. Hence, by [Reference Zhang and Wei35, Theorem 3.5], we deduce that there exists a quasicotilting R-module T such that
${\mathrm {Sub}}\mathscr {U}$
. Hence, by [Reference Zhang and Wei35, Theorem 3.5], we deduce that there exists a quasicotilting R-module T such that
![]() ${\mathrm {Sub}} \mathscr {U}={\mathrm {Cogen}}(T)$
.
${\mathrm {Sub}} \mathscr {U}={\mathrm {Cogen}}(T)$
.
Definition 7.2.7 Let
![]() $\mathscr {A}$
be an abelian category with enough injective objects. Let
$\mathscr {A}$
be an abelian category with enough injective objects. Let
![]() $\mathscr {U}$
and
$\mathscr {U}$
and
![]() $\mathscr {U}'$
be two support
$\mathscr {U}'$
be two support
![]() $\tau ^-$
-titling subcategories of
$\tau ^-$
-titling subcategories of
![]() $\mathscr {A}$
. We say that
$\mathscr {A}$
. We say that
![]() $\mathscr {U}$
and
$\mathscr {U}$
and
![]() $\mathscr {U}'$
are equivalent if
$\mathscr {U}'$
are equivalent if
![]() ${\mathrm {Sub}} \mathscr {U}={\mathrm {Sub}} \mathscr {U}'.$
${\mathrm {Sub}} \mathscr {U}={\mathrm {Sub}} \mathscr {U}'.$
Now we can state the main theorem of this subsection which is the dual of Theorem 7.1.10. Recall that, by [Reference Zhang and Wei35, p. 12], two quasicotilting modules
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are equivalent if
$T_2$
are equivalent if
![]() ${\mathrm {Prod}}(T_1)={\mathrm {Prod}}(T_2)$
.
${\mathrm {Prod}}(T_1)={\mathrm {Prod}}(T_2)$
.
Theorem 7.2.8 There is a bijection between the equivalence classes of support
![]() $\tau ^-$
-tilting subcategories of
$\tau ^-$
-tilting subcategories of
![]() $\mathrm{Mod}\mbox {-}R$
and the equivalence classes of cosilting R-modules.
$\mathrm{Mod}\mbox {-}R$
and the equivalence classes of cosilting R-modules.
Proof. The result follows by Propositions 7.2.6 and 7.2.4 together with [Reference Zhang and Wei34, Theorem 4.18].
8 Applications to quiver representations
This section is devoted to producing support
![]() $\tau $
-tilting subcategories of the category of representation of quivers. We divide the section into three subsections. In the first subsection, we recall some known definitions and properties of the category
$\tau $
-tilting subcategories of the category of representation of quivers. We divide the section into three subsections. In the first subsection, we recall some known definitions and properties of the category
![]() $\mathrm {Rep}(Q, \mathscr {A})$
of representations of a finite acyclic quiver Q over an abelian category
$\mathrm {Rep}(Q, \mathscr {A})$
of representations of a finite acyclic quiver Q over an abelian category
![]() $\mathscr {A}$
with enough projective objects. In the second subsection, we produce support
$\mathscr {A}$
with enough projective objects. In the second subsection, we produce support
![]() $\tau $
-tilting subcategories in
$\tau $
-tilting subcategories in
![]() $\mathrm {Rep}(Q, \mathscr {A})$
from certain
$\mathrm {Rep}(Q, \mathscr {A})$
from certain
![]() $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
![]() $\mathscr {A}$
. Finally, in the last subsection, we construct (co)silting modules in
$\mathscr {A}$
. Finally, in the last subsection, we construct (co)silting modules in
![]() $\mathrm{Mod}\mbox {-}RQ$
from (co)silting modules in
$\mathrm{Mod}\mbox {-}RQ$
from (co)silting modules in
![]() $\mathrm{Mod}\mbox {-}R$
.
$\mathrm{Mod}\mbox {-}R$
.
8.1 Notions on quiver representations
Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects
$\mathscr {A}$
be an abelian category with enough projective objects
![]() ${\mathrm {Prj}}(\mathscr {A})$
and
${\mathrm {Prj}}(\mathscr {A})$
and
![]() $Q=(Q_0, Q_1)$
be a finite acyclic quiver with vertex set
$Q=(Q_0, Q_1)$
be a finite acyclic quiver with vertex set
![]() $Q_0$
of cardinality n and arrow set
$Q_0$
of cardinality n and arrow set
![]() $Q_1$
. An arrow
$Q_1$
. An arrow
![]() $\alpha \in Q_1$
of source
$\alpha \in Q_1$
of source
![]() $i=s(\alpha )$
and target
$i=s(\alpha )$
and target
![]() $j=t(\alpha )$
is usually denoted by
$j=t(\alpha )$
is usually denoted by
![]() $\alpha : i\rightarrow j$
. We denote by
$\alpha : i\rightarrow j$
. We denote by
![]() $\mathrm {Rep}(Q, \mathscr {A})$
the category of representations of Q in
$\mathrm {Rep}(Q, \mathscr {A})$
the category of representations of Q in
![]() $\mathscr {A}$
. An object X in
$\mathscr {A}$
. An object X in
![]() $\mathrm {Rep}(Q, \mathscr {A})$
is defined by the following data:
$\mathrm {Rep}(Q, \mathscr {A})$
is defined by the following data:
-
1. To each vertex,
 $i\in Q_0$
is associated an object
$i\in Q_0$
is associated an object
 $X_i$
in
$X_i$
in
 $\mathscr {A}$
.
$\mathscr {A}$
. -
2. To each arrow,
 $\alpha : i\rightarrow j$
in
$\alpha : i\rightarrow j$
in
 $Q_1$
is associated a morphism
$Q_1$
is associated a morphism
 $X_\alpha : X_i\longrightarrow X_j$
.
$X_\alpha : X_i\longrightarrow X_j$
.
A morphism
![]() $\varphi : X \longrightarrow Y$
in
$\varphi : X \longrightarrow Y$
in
![]() $\mathrm {Rep}(Q,\mathscr {A})$
is a family
$\mathrm {Rep}(Q,\mathscr {A})$
is a family
![]() $\lbrace \varphi _i: X_i\longrightarrow Y_i \rbrace _{ i\in Q_0}$
of morphisms in
$\lbrace \varphi _i: X_i\longrightarrow Y_i \rbrace _{ i\in Q_0}$
of morphisms in
![]() $\mathscr {A}$
such that for each arrow
$\mathscr {A}$
such that for each arrow
![]() $\alpha : i\longrightarrow j$
in
$\alpha : i\longrightarrow j$
in
![]() $Q_1$
, the diagram
$Q_1$
, the diagram

is commutative.
The category
![]() $\mathrm {Rep}(Q, \mathscr {A})$
is an abelian category. Kernels, cokernels, and images in
$\mathrm {Rep}(Q, \mathscr {A})$
is an abelian category. Kernels, cokernels, and images in
![]() $\mathrm { Rep}(Q,\mathscr {A})$
are computed vertexwise in
$\mathrm { Rep}(Q,\mathscr {A})$
are computed vertexwise in
![]() $\mathscr {A}$
. A sequence
$\mathscr {A}$
. A sequence
![]() $X \longrightarrow Y \longrightarrow Z$
in
$X \longrightarrow Y \longrightarrow Z$
in
![]() $\mathrm {Rep}(Q,\mathscr {A})$
is exact if and only if for every vertex
$\mathrm {Rep}(Q,\mathscr {A})$
is exact if and only if for every vertex
![]() $i \in Q_0$
, the sequence
$i \in Q_0$
, the sequence
![]() $X_i\longrightarrow Y_i\longrightarrow Z_i$
is exact in
$X_i\longrightarrow Y_i\longrightarrow Z_i$
is exact in
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
For each vertex
![]() $i\in Q_0$
, there exists the evaluation functor
$i\in Q_0$
, there exists the evaluation functor
 $$\begin{align*}e_i: \mathrm{Rep}(Q, \mathscr{A})&\longrightarrow \mathscr{A}\\X&\mapsto X_i\end{align*}$$
$$\begin{align*}e_i: \mathrm{Rep}(Q, \mathscr{A})&\longrightarrow \mathscr{A}\\X&\mapsto X_i\end{align*}$$
which sends each representation
![]() $X\in \mathrm {Rep}(Q, \mathscr {A})$
to the object
$X\in \mathrm {Rep}(Q, \mathscr {A})$
to the object
![]() $X_i\in \mathscr {A}$
at vertex i. It is clear that the evaluation functor
$X_i\in \mathscr {A}$
at vertex i. It is clear that the evaluation functor
![]() $e_i$
is exact and it has an exact left and also an exact right adjoint, which will be denoted by
$e_i$
is exact and it has an exact left and also an exact right adjoint, which will be denoted by
![]() $e_i^{\lambda }$
and
$e_i^{\lambda }$
and
![]() $e_i^\rho $
, respectively. Let us recall the constructions of
$e_i^\rho $
, respectively. Let us recall the constructions of
![]() $e_i^{\lambda },e_i^\rho : \mathscr {A}\longrightarrow \mathrm {Rep}(Q, \mathscr {A})$
more explicitly (cf. [Reference Holm and Jørgensen25]).
$e_i^{\lambda },e_i^\rho : \mathscr {A}\longrightarrow \mathrm {Rep}(Q, \mathscr {A})$
more explicitly (cf. [Reference Holm and Jørgensen25]).
Let
![]() $A\in \mathscr {A}$
. Then
$A\in \mathscr {A}$
. Then
![]() $e_i^{\lambda }(A)_j= \bigoplus _{Q(i, j)} A$
, where
$e_i^{\lambda }(A)_j= \bigoplus _{Q(i, j)} A$
, where
![]() $Q(i, j)$
denotes the set of paths starting in i and ending in j. The morphisms are natural inclusions, that is, for any arrow
$Q(i, j)$
denotes the set of paths starting in i and ending in j. The morphisms are natural inclusions, that is, for any arrow
![]() $\alpha : j\longrightarrow k$
, we set
$\alpha : j\longrightarrow k$
, we set
![]() $e_i^{\lambda }(A)_\alpha : \bigoplus _{Q(i, j)} A\longrightarrow \bigoplus _{Q(i, k)} A$
.
$e_i^{\lambda }(A)_\alpha : \bigoplus _{Q(i, j)} A\longrightarrow \bigoplus _{Q(i, k)} A$
.
The right adjoint
![]() $e_i^\rho $
is defined dually. Let
$e_i^\rho $
is defined dually. Let
![]() $A\in \mathscr {A}$
. Then
$A\in \mathscr {A}$
. Then
![]() $e_i^\rho (A)_j=\bigoplus _{Q(j, i)} A$
. The morphisms are natural projections. Moreover, the functor
$e_i^\rho (A)_j=\bigoplus _{Q(j, i)} A$
. The morphisms are natural projections. Moreover, the functor
![]() $e_i^\rho $
has a right adjoint, which will be denoted by
$e_i^\rho $
has a right adjoint, which will be denoted by
![]() $Re_i^\rho $
.
$Re_i^\rho $
.
One can show that the sets
are sets of projective generators and injective cogenerators for the category
![]() $\mathrm {Rep}(Q, \mathscr {A})$
, respectively. For details of the proofs, see, e.g., [Reference Enochs and Estrada20, Reference Enochs, Estrada and Rozas21].
$\mathrm {Rep}(Q, \mathscr {A})$
, respectively. For details of the proofs, see, e.g., [Reference Enochs and Estrada20, Reference Enochs, Estrada and Rozas21].
8.2 Constructing
 $\tau $
-tilting subcategories of
$\tau $
-tilting subcategories of
 $\mathrm {Rep}(Q, \mathscr {A})$
$\mathrm {Rep}(Q, \mathscr {A})$
Our aim in this subsection is to provide a systematic technique to construct, starting from a certain
![]() $\tau $
-tilting subcategory
$\tau $
-tilting subcategory
![]() $\mathscr {T}$
of an abelian category
$\mathscr {T}$
of an abelian category
![]() $\mathscr {A}$
, a new
$\mathscr {A}$
, a new
![]() $\tau $
-tilting subcategory in the category
$\tau $
-tilting subcategory in the category
![]() $\mathrm {Rep}(Q, \mathscr {A})$
of representations of a finite and acyclic quiver Q in
$\mathrm {Rep}(Q, \mathscr {A})$
of representations of a finite and acyclic quiver Q in
![]() $\mathscr {A}$
. For the proof of the main result of this subsection, we need the following lemma. Although it seems that it is known to the experts, we could not find a reference. So we provide proof for the sake of completeness.
$\mathscr {A}$
. For the proof of the main result of this subsection, we need the following lemma. Although it seems that it is known to the experts, we could not find a reference. So we provide proof for the sake of completeness.
Lemma 8.2.1 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects, and let
$\mathscr {A}$
be an abelian category with enough projective objects, and let
![]() $Q=(Q_0, Q_1)$
be a finite and acyclic quiver. Then, for every
$Q=(Q_0, Q_1)$
be a finite and acyclic quiver. Then, for every
![]() $X, Y \in \mathrm {Rep}(Q, \mathscr {A})$
, there exists the long exact sequence
$X, Y \in \mathrm {Rep}(Q, \mathscr {A})$
, there exists the long exact sequence
 $$ \begin{align*} 0 \longrightarrow & \ {\mathrm{Hom}}_{\mathscr{R}}(X, Y)\longrightarrow \bigoplus_{r\in Q_0} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_r) \stackrel{\varphi}\longrightarrow \bigoplus_{\alpha: r\rightarrow l} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_l) \\ \longrightarrow & \ {\mathrm{Ext}}^1_{\mathscr{R}}(X, Y) \ \longrightarrow \ \bigoplus_{r\in Q_0}{\mathrm{Ext}}^1_{\mathscr{A}}(X_r, Y_r) \ \longrightarrow \bigoplus_{\alpha: r\rightarrow l}{\mathrm{Ext}}^1_{\mathscr{A}}(X_r, Y_l) \\ \longrightarrow & \ {\mathrm{Ext}}^2_{\mathscr{R}}(X, Y) \ \longrightarrow \cdots, \end{align*} $$
$$ \begin{align*} 0 \longrightarrow & \ {\mathrm{Hom}}_{\mathscr{R}}(X, Y)\longrightarrow \bigoplus_{r\in Q_0} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_r) \stackrel{\varphi}\longrightarrow \bigoplus_{\alpha: r\rightarrow l} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_l) \\ \longrightarrow & \ {\mathrm{Ext}}^1_{\mathscr{R}}(X, Y) \ \longrightarrow \ \bigoplus_{r\in Q_0}{\mathrm{Ext}}^1_{\mathscr{A}}(X_r, Y_r) \ \longrightarrow \bigoplus_{\alpha: r\rightarrow l}{\mathrm{Ext}}^1_{\mathscr{A}}(X_r, Y_l) \\ \longrightarrow & \ {\mathrm{Ext}}^2_{\mathscr{R}}(X, Y) \ \longrightarrow \cdots, \end{align*} $$
where here and throughout we set
![]() $\mathscr {R}:=\mathrm {Rep}(Q, \mathscr {A})$
.
$\mathscr {R}:=\mathrm {Rep}(Q, \mathscr {A})$
.
Proof. Let
![]() $X \in \mathscr {R}:=\mathrm {Rep}(Q, \mathscr {A})$
. By [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 3.5], there exists a short exact sequence
$X \in \mathscr {R}:=\mathrm {Rep}(Q, \mathscr {A})$
. By [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 3.5], there exists a short exact sequence
which is natural in X. By applying the functor
![]() ${\mathrm {Hom}}_{\mathscr {R}}(-,Y)$
to this sequence, we get the following long exact sequence:
${\mathrm {Hom}}_{\mathscr {R}}(-,Y)$
to this sequence, we get the following long exact sequence:
 $$ \begin{align*} 0 \longrightarrow & \ {\mathrm{Hom}}_{\mathscr{R}}(X, Y) \longrightarrow \bigoplus_{r\in Q_0}{\mathrm{Hom}}_{\mathscr{R}}( e_r^{\lambda}(X_r), Y)\longrightarrow \bigoplus_{\alpha:r\rightarrow l}{\mathrm{Hom}}_{\mathscr{R}}(e_l^{\lambda}(X_r), Y)\\ \longrightarrow & \ {\mathrm{Ext}}^1_{\mathscr{R}}(X, Y) \ \ \longrightarrow\bigoplus_{r\in Q_0}{\mathrm{Ext}}^1_{\mathscr{R}}( e_r^{\lambda}(X_r), Y) \ \longrightarrow \bigoplus_{\alpha:r\rightarrow l}{\mathrm{Ext}}^1_{\mathscr{R}}(e_l^{\lambda}(X_r), Y)\\ \longrightarrow & \ {\mathrm{Ext}}^2_{\mathscr{R}}(X, Y) \ \ \longrightarrow \cdots. \end{align*} $$
$$ \begin{align*} 0 \longrightarrow & \ {\mathrm{Hom}}_{\mathscr{R}}(X, Y) \longrightarrow \bigoplus_{r\in Q_0}{\mathrm{Hom}}_{\mathscr{R}}( e_r^{\lambda}(X_r), Y)\longrightarrow \bigoplus_{\alpha:r\rightarrow l}{\mathrm{Hom}}_{\mathscr{R}}(e_l^{\lambda}(X_r), Y)\\ \longrightarrow & \ {\mathrm{Ext}}^1_{\mathscr{R}}(X, Y) \ \ \longrightarrow\bigoplus_{r\in Q_0}{\mathrm{Ext}}^1_{\mathscr{R}}( e_r^{\lambda}(X_r), Y) \ \longrightarrow \bigoplus_{\alpha:r\rightarrow l}{\mathrm{Ext}}^1_{\mathscr{R}}(e_l^{\lambda}(X_r), Y)\\ \longrightarrow & \ {\mathrm{Ext}}^2_{\mathscr{R}}(X, Y) \ \ \longrightarrow \cdots. \end{align*} $$
Now the result follows in view of the adjoint pair
![]() $(e_i^{\lambda }, e_i)$
and using the fact that the adjunction between
$(e_i^{\lambda }, e_i)$
and using the fact that the adjunction between
![]() $e_i^{\lambda }$
and
$e_i^{\lambda }$
and
![]() $e_i$
extends to
$e_i$
extends to
![]() ${\mathrm {Ext}}^t$
, for all
${\mathrm {Ext}}^t$
, for all
![]() $t \geq i$
(see [Reference Holm and Jørgensen25, Proposition 5.2]).
$t \geq i$
(see [Reference Holm and Jørgensen25, Proposition 5.2]).
Now we can state and prove the main result of this part.
Theorem 8.2.2 Let
![]() $\mathscr {A}$
be an abelian category with enough projective objects, and let
$\mathscr {A}$
be an abelian category with enough projective objects, and let
![]() $Q=(Q_0, Q_1)$
be a finite and acyclic quiver. Let
$Q=(Q_0, Q_1)$
be a finite and acyclic quiver. Let
![]() $\mathscr {T}$
be a support
$\mathscr {T}$
be a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
such that the induced torsion pair
$\mathscr {A}$
such that the induced torsion pair
![]() $({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is hereditary. Then
$({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
is hereditary. Then
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm {Rep}(Q, \mathscr {A})$
.
$\mathrm {Rep}(Q, \mathscr {A})$
.
Proof. We show the validity of conditions of Definition 3.1. For the first condition, let
![]() $i, j\in Q_0$
and
$i, j\in Q_0$
and
![]() $T\in \mathscr {T}$
. We show that
$T\in \mathscr {T}$
. We show that
Set
![]() $X:=e_i^{\rho }(T)$
and pick
$X:=e_i^{\rho }(T)$
and pick
![]() $Y\in {\mathrm {Fac}}(e_j^{\rho }(T))$
. Then, for every
$Y\in {\mathrm {Fac}}(e_j^{\rho }(T))$
. Then, for every
![]() $r\in Q_0$
,
$r\in Q_0$
,
![]() $X_r$
is the sum of some finite copies of T, maybe zero, and
$X_r$
is the sum of some finite copies of T, maybe zero, and
![]() $Y_r$
is in
$Y_r$
is in
![]() ${\mathrm {Fac}}(T)$
. Moreover, for every
${\mathrm {Fac}}(T)$
. Moreover, for every
![]() $\alpha : r\rightarrow l\in Q_1$
,
$\alpha : r\rightarrow l\in Q_1$
,
![]() $Y_\alpha : Y_r\longrightarrow Y_l$
is an epimorphism. Hence, since by assumption
$Y_\alpha : Y_r\longrightarrow Y_l$
is an epimorphism. Hence, since by assumption
![]() ${\mathrm {Fac}}(\mathscr {T})$
is closed under subobjects, we deduce that
${\mathrm {Fac}}(\mathscr {T})$
is closed under subobjects, we deduce that
![]() ${\mathrm {Ker}} Y_\alpha \in {\mathrm {Fac}}(T)$
. This, in particular, implies that for every
${\mathrm {Ker}} Y_\alpha \in {\mathrm {Fac}}(T)$
. This, in particular, implies that for every
![]() $T \in \mathscr {T}$
, the induced morphism
$T \in \mathscr {T}$
, the induced morphism
is an epimorphism.
Hence, in the exact sequence
 $$\begin{align*}\bigoplus_{r\in Q_0} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_r) \stackrel{\varphi}\longrightarrow \bigoplus_{\alpha: r\rightarrow l} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_l) \longrightarrow \\ {\mathrm{Ext}}^1_{\mathscr{R}}(X, Y)\longrightarrow \bigoplus_{r\in Q_0}{\mathrm{Ext}}^1_{\mathscr{A}}(X_r, Y_r),\end{align*}$$
$$\begin{align*}\bigoplus_{r\in Q_0} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_r) \stackrel{\varphi}\longrightarrow \bigoplus_{\alpha: r\rightarrow l} {\mathrm{Hom}}_{\mathscr{A}}(X_r, Y_l) \longrightarrow \\ {\mathrm{Ext}}^1_{\mathscr{R}}(X, Y)\longrightarrow \bigoplus_{r\in Q_0}{\mathrm{Ext}}^1_{\mathscr{A}}(X_r, Y_r),\end{align*}$$
of the above lemma, we deduce that
![]() $\varphi $
is an epimorphism. So, to show the result, it is enough to show that
$\varphi $
is an epimorphism. So, to show the result, it is enough to show that
This follows from the fact
![]() ${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))$
, because
${\mathrm {Ext}}^1_{\mathscr {A}}(\mathscr {T}, {\mathrm {Fac}}(\mathscr {T}))$
, because
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
and the fact that
$\mathscr {A}$
and the fact that
Now we show the validity of the second condition. It is enough to show it only for the projective generators of
![]() $\mathrm {Rep}(Q, \mathscr {A})$
, i.e., for representations of the form
$\mathrm {Rep}(Q, \mathscr {A})$
, i.e., for representations of the form
![]() $e_i^{\lambda }(P)$
, where P is a projective object in
$e_i^{\lambda }(P)$
, where P is a projective object in
![]() $\mathscr {A}$
. Let
$\mathscr {A}$
. Let
![]() $\lbrace \rho _1, \ldots , \rho _k \rbrace $
be the set of all longest paths in Q starting from i. Since
$\lbrace \rho _1, \ldots , \rho _k \rbrace $
be the set of all longest paths in Q starting from i. Since
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathscr {A}$
, for P there exists an exact sequence
$\mathscr {A}$
, for P there exists an exact sequence
![]() $P\stackrel {f}\longrightarrow T^0\stackrel {g}\longrightarrow T^1\longrightarrow 0$
, such that
$P\stackrel {f}\longrightarrow T^0\stackrel {g}\longrightarrow T^1\longrightarrow 0$
, such that
![]() $T^0, T^1\in \mathscr {T}$
and f is a left
$T^0, T^1\in \mathscr {T}$
and f is a left
![]() $\mathscr {T}$
-approximation of P. Since
$\mathscr {T}$
-approximation of P. Since
![]() ${\mathrm {Fac}}(\mathscr {T})$
is closed under subobjects,
${\mathrm {Fac}}(\mathscr {T})$
is closed under subobjects,
![]() ${\mathrm {Ker}} g \in {\mathrm {Fac}}(\mathscr {T})$
and so the induced short exact sequence
${\mathrm {Ker}} g \in {\mathrm {Fac}}(\mathscr {T})$
and so the induced short exact sequence
splits and so
![]() ${\mathrm {Ker}} g\in \mathscr {T}$
. Take the exact sequence
${\mathrm {Ker}} g\in \mathscr {T}$
. Take the exact sequence
 $$\begin{align*}e^{\lambda}_{i}(P)\stackrel{\psi}\longrightarrow \bigoplus_{q=1}^ k e^\rho_{t(\rho_q)}(T^0)\longrightarrow \bigoplus_{q=1}^k e^\rho_{t(\rho_q)}(T^1)\oplus \bigoplus_{\alpha \in \mathfrak{I} }e^\rho_{s(\alpha)}({\mathrm{Ker}} g)\longrightarrow 0,\end{align*}$$
$$\begin{align*}e^{\lambda}_{i}(P)\stackrel{\psi}\longrightarrow \bigoplus_{q=1}^ k e^\rho_{t(\rho_q)}(T^0)\longrightarrow \bigoplus_{q=1}^k e^\rho_{t(\rho_q)}(T^1)\oplus \bigoplus_{\alpha \in \mathfrak{I} }e^\rho_{s(\alpha)}({\mathrm{Ker}} g)\longrightarrow 0,\end{align*}$$
where
![]() $\mathfrak {I}\subset Q_1$
is the set of arrows
$\mathfrak {I}\subset Q_1$
is the set of arrows
![]() $\alpha $
of Q such that
$\alpha $
of Q such that
![]() $\alpha $
is not part of any path in the set
$\alpha $
is not part of any path in the set
![]() $\lbrace \rho _1, \ldots , \rho _k \rbrace $
but there is a path in that set passing through
$\lbrace \rho _1, \ldots , \rho _k \rbrace $
but there is a path in that set passing through
![]() $t(\alpha )$
. An easy verification shows that this is the desired sequence for
$t(\alpha )$
. An easy verification shows that this is the desired sequence for
![]() $e^{\lambda }_i(P)$
. In particular,
$e^{\lambda }_i(P)$
. In particular,
![]() $\psi $
is a left
$\psi $
is a left
![]() $\mathbb {T}$
-approximation of
$\mathbb {T}$
-approximation of
![]() $e^{\lambda }_{i}(P)$
.
$e^{\lambda }_{i}(P)$
.
To complete the proof, we have to show that
![]() $\mathbb {T}$
is a contravariantly finite subcategory of
$\mathbb {T}$
is a contravariantly finite subcategory of
![]() $\mathrm { Rep}(Q, \mathscr {A})$
. Let
$\mathrm { Rep}(Q, \mathscr {A})$
. Let
![]() $X \in \mathrm {Rep}(Q, \mathscr {A})$
. For each i, consider a right
$X \in \mathrm {Rep}(Q, \mathscr {A})$
. For each i, consider a right
![]() $\mathscr {T}$
-approximation
$\mathscr {T}$
-approximation
![]() $\pi ^i: T^i \longrightarrow Re_i^\rho (X)$
, where
$\pi ^i: T^i \longrightarrow Re_i^\rho (X)$
, where
![]() $Re_i^\rho $
is the right adjoint of
$Re_i^\rho $
is the right adjoint of
![]() $e_i^\rho $
. Following the same argument as in [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9], one can show that
$e_i^\rho $
. Following the same argument as in [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9], one can show that
is a right
![]() $\mathbb {T}$
-approximation of X.
$\mathbb {T}$
-approximation of X.
The examples below provide situations where the torsion pair
![]() $({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
induced by the support
$({\mathrm {Fac}}(\mathscr {T}), \mathscr {T}^{\perp _0})$
induced by the support
![]() $\tau $
-tilting subcategory
$\tau $
-tilting subcategory
![]() $\mathscr {T}$
of
$\mathscr {T}$
of
![]() $\mathscr {A}$
is hereditary.
$\mathscr {A}$
is hereditary.
Example 8.2.3 Let
![]() $\Lambda $
be an Artin algebra, and let S be a simple injective object in
$\Lambda $
be an Artin algebra, and let S be a simple injective object in
![]() ${\mathrm {{mod\mbox {-}}}}\Lambda $
. Then
${\mathrm {{mod\mbox {-}}}}\Lambda $
. Then
![]() ${\mathrm {add}}(S)$
is a support
${\mathrm {add}}(S)$
is a support
![]() $\tau $
-tilting subcategory such that
$\tau $
-tilting subcategory such that
![]() ${\mathrm {Fac}}(S)={\mathrm {add}}(S)$
is closed under subobjects.
${\mathrm {Fac}}(S)={\mathrm {add}}(S)$
is closed under subobjects.
Example 8.2.4 Let A be a finite-dimensional algebra, let e be an idempotent of A, and let
![]() $B=A/AeA$
. Let
$B=A/AeA$
. Let
![]() $Q=(Q_0, Q_1)$
be a finite and acyclic quiver. By [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9], we have
$Q=(Q_0, Q_1)$
be a finite and acyclic quiver. By [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9], we have
![]() $\mathscr {T}={\mathrm {add}} (\lbrace e_i^\rho (B) \vert i\in Q_0\rbrace )$
is a tilting subcategory in
$\mathscr {T}={\mathrm {add}} (\lbrace e_i^\rho (B) \vert i\in Q_0\rbrace )$
is a tilting subcategory in
![]() $\mathrm {Rep}(Q, {\mathrm {{mod\mbox {-}}}} B)$
. On the other hand, it is obvious that
$\mathrm {Rep}(Q, {\mathrm {{mod\mbox {-}}}} B)$
. On the other hand, it is obvious that
![]() ${\mathrm {add}}(B)$
is a support
${\mathrm {add}}(B)$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() ${\mathrm {{mod\mbox {-}}}} A$
and
${\mathrm {{mod\mbox {-}}}} A$
and
![]() ${\mathrm {Fac}}({\mathrm {add}}(B))={\mathrm {{mod\mbox {-}}}} B$
is closed under subobjects. So, by Theorem 8.2.2,
${\mathrm {Fac}}({\mathrm {add}}(B))={\mathrm {{mod\mbox {-}}}} B$
is closed under subobjects. So, by Theorem 8.2.2,
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting of
$\tau $
-tilting of
![]() $\mathrm {Rep}(Q, {\mathrm {{mod\mbox {-}}}} A)$
.
$\mathrm {Rep}(Q, {\mathrm {{mod\mbox {-}}}} A)$
.
We end this subsection with the following example which is also an application of Theorem 3.5.
Example 8.2.5 Let Q be a finite and acyclic quiver, and let
![]() $Q'$
be a full subquiver of Q. Then it is easy to see that
$Q'$
be a full subquiver of Q. Then it is easy to see that
![]() $\mathrm {Rep}(Q', \mathscr {A})$
is a wide and functorially finite torsion class of
$\mathrm {Rep}(Q', \mathscr {A})$
is a wide and functorially finite torsion class of
![]() $\mathrm {Rep}(Q, A)$
. By [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9],
$\mathrm {Rep}(Q, A)$
. By [Reference Bauer, Botnan, Oppermann and Steen7, Proposition 3.9],
![]() $\mathscr {T}={\mathrm {add}}(\lbrace e_i^\rho (P)\ \vert i\in Q^{\prime }_0, P\in {\mathrm {Prj}}(\mathscr {A})\rbrace )$
is a tilting subcategory of
$\mathscr {T}={\mathrm {add}}(\lbrace e_i^\rho (P)\ \vert i\in Q^{\prime }_0, P\in {\mathrm {Prj}}(\mathscr {A})\rbrace )$
is a tilting subcategory of
![]() $\mathrm { Rep}(Q', \mathscr {A})$
. So, by Theorem 3.5,
$\mathrm { Rep}(Q', \mathscr {A})$
. So, by Theorem 3.5,
![]() $\mathscr {T}$
is a support
$\mathscr {T}$
is a support
![]() $\tau $
-tilting subcategory of
$\tau $
-tilting subcategory of
![]() $\mathrm {Rep}(Q, \mathscr {A})$
.
$\mathrm {Rep}(Q, \mathscr {A})$
.
8.3 (Co)silting objects in
 $\mathrm {Rep}(Q, \mathscr {A})$
$\mathrm {Rep}(Q, \mathscr {A})$
Let R be an associative ring with unity, and let Q be a finite and acyclic quiver. In this subsection, we construct silting (resp. cosilting) objects in the category of representations of Q in
![]() $\mathrm{Mod}\mbox {-} R$
,
$\mathrm{Mod}\mbox {-} R$
,
![]() $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
, from silting (resp. cosilting) modules in
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
, from silting (resp. cosilting) modules in
![]() $\mathrm{Mod}\mbox {-} R$
. Note that
$\mathrm{Mod}\mbox {-} R$
. Note that
![]() $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
is equivalent to the
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
is equivalent to the
![]() $\mathrm{Mod}\mbox {-}RQ$
, where
$\mathrm{Mod}\mbox {-}RQ$
, where
![]() $RQ$
denotes the path algebra of Q over R. So, by a silting (resp. cosilting) object in
$RQ$
denotes the path algebra of Q over R. So, by a silting (resp. cosilting) object in
![]() $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
, we mean a silting (resp. cosilting) module in
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
, we mean a silting (resp. cosilting) module in
![]() $\mathrm{Mod}\mbox {-}RQ$
.
$\mathrm{Mod}\mbox {-}RQ$
.
Theorem 8.3.1 Let
![]() $Q=(Q_0, Q_1)$
be a finite and acyclic quiver.
$Q=(Q_0, Q_1)$
be a finite and acyclic quiver.
-
(i) Let S be a silting module in
 $\mathrm{Mod}\mbox {-}R$
. Let
$\mathrm{Mod}\mbox {-}R$
. Let
 $i\in Q_0$
be an arbitrary vertex of Q. Then
$i\in Q_0$
be an arbitrary vertex of Q. Then
 $e_i^{\lambda }(S)$
is a silting object in
$e_i^{\lambda }(S)$
is a silting object in
 $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
.
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. -
(ii) Let C be a cosilting module in
 $\mathrm{Mod}\mbox {-}R$
. Let
$\mathrm{Mod}\mbox {-}R$
. Let
 $i\in Q_0$
be an arbitrary vertex of Q. Then
$i\in Q_0$
be an arbitrary vertex of Q. Then
 $e_i^\rho (C)$
is a cosilting object in
$e_i^\rho (C)$
is a cosilting object in
 $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
.
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
.
Proof.
![]() $(i)$
Let S be a silting R-module. By definition, there exists a projective presentation
$(i)$
Let S be a silting R-module. By definition, there exists a projective presentation
of S such that
![]() $\mathscr {D}_\sigma ={\mathrm {Gen}}(S)$
. By applying the exact functor
$\mathscr {D}_\sigma ={\mathrm {Gen}}(S)$
. By applying the exact functor
![]() $e_i^{\lambda }$
on the projective presentation of S and using the fact that
$e_i^{\lambda }$
on the projective presentation of S and using the fact that
![]() $e_i^{\lambda }$
is an exact functor that preserves projectives, we get the projective presentation
$e_i^{\lambda }$
is an exact functor that preserves projectives, we get the projective presentation
of
![]() $e_i^{\lambda }(S)$
. To complete the proof, we show that
$e_i^{\lambda }(S)$
. To complete the proof, we show that
![]() $\mathscr {D}_{e_i^{\lambda }(\sigma )}={\mathrm {Gen}}(e_i^{\lambda }(S))$
.
$\mathscr {D}_{e_i^{\lambda }(\sigma )}={\mathrm {Gen}}(e_i^{\lambda }(S))$
.
Let
![]() $X \in \mathscr {D}_{e_i^{\lambda }(\sigma )}$
. So there exists an epimorphism
$X \in \mathscr {D}_{e_i^{\lambda }(\sigma )}$
. So there exists an epimorphism
where
![]() $\mathscr {R}$
means
$\mathscr {R}$
means
![]() $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. The adjoint pair
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. The adjoint pair
![]() $(e_i^{\lambda }, e_i)$
induces the epimorphism
$(e_i^{\lambda }, e_i)$
induces the epimorphism
This, in turn, implies that
![]() $X_i \in \mathscr {D}_\sigma ={\mathrm {Gen}}(S)$
. Therefore,
$X_i \in \mathscr {D}_\sigma ={\mathrm {Gen}}(S)$
. Therefore,
![]() $e_i^{\lambda }(X_i) \in e_i^{\lambda }({\mathrm {Gen}}(S))$
. On the other hand, by [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 3.5], there exists an epimorphism
$e_i^{\lambda }(X_i) \in e_i^{\lambda }({\mathrm {Gen}}(S))$
. On the other hand, by [Reference Bauer, Botnan, Oppermann and Steen7, Lemma 3.5], there exists an epimorphism
![]() $\bigoplus _{i\in Q_0} e_i^{\lambda }(X_i)\longrightarrow X\longrightarrow 0$
which shows that
$\bigoplus _{i\in Q_0} e_i^{\lambda }(X_i)\longrightarrow X\longrightarrow 0$
which shows that
![]() $X\in e_i^{\lambda }({\mathrm {Gen}}(S))$
. But it follows directly from the definition of
$X\in e_i^{\lambda }({\mathrm {Gen}}(S))$
. But it follows directly from the definition of
![]() $e_i^{\lambda }$
that
$e_i^{\lambda }$
that
![]() $e_i^{\lambda }({\mathrm {Gen}}(S)) = {\mathrm {Gen}}(e_i^{\lambda }(S))$
. Thus,
$e_i^{\lambda }({\mathrm {Gen}}(S)) = {\mathrm {Gen}}(e_i^{\lambda }(S))$
. Thus,
![]() $\mathscr {D}_{e_i^{\lambda }(\sigma )}\subseteq {\mathrm {Gen}}(e_i^{\lambda }(S))$
.
$\mathscr {D}_{e_i^{\lambda }(\sigma )}\subseteq {\mathrm {Gen}}(e_i^{\lambda }(S))$
.
To see the reverse inclusion, let
![]() $X\in e_i^{\lambda }({\mathrm {Gen}}(S))$
. So
$X\in e_i^{\lambda }({\mathrm {Gen}}(S))$
. So
![]() $X=e_i^{\lambda }(U)$
such that
$X=e_i^{\lambda }(U)$
such that
![]() $U\in {\mathrm {Gen}}(S)$
. Since
$U\in {\mathrm {Gen}}(S)$
. Since
![]() ${\mathrm {Gen}}(S)=\mathscr {D}_\sigma $
, we have
${\mathrm {Gen}}(S)=\mathscr {D}_\sigma $
, we have
![]() $U\in \mathscr {D}_\sigma $
. Therefore, there exists an epimorphism
$U\in \mathscr {D}_\sigma $
. Therefore, there exists an epimorphism
By the using of adjoint properties of adjoint pair
![]() $(e_i^{\lambda }, e_i)$
, we have an epimorphism
$(e_i^{\lambda }, e_i)$
, we have an epimorphism
which shows that
![]() $X\in \mathscr {D}_{e_i^{\lambda }(\sigma )}$
. So we show that
$X\in \mathscr {D}_{e_i^{\lambda }(\sigma )}$
. So we show that
![]() $e_i^{\lambda }({\mathrm {Gen}}(S))= {\mathrm {Gen}}(e_i^{\lambda }(S)) \subseteq \mathscr {D}_{e_i^{\lambda }(\sigma )}$
. Hence, the proof is complete.
$e_i^{\lambda }({\mathrm {Gen}}(S))= {\mathrm {Gen}}(e_i^{\lambda }(S)) \subseteq \mathscr {D}_{e_i^{\lambda }(\sigma )}$
. Hence, the proof is complete.
![]() $(ii)$
The proof is just dual of the proof of part
$(ii)$
The proof is just dual of the proof of part
![]() $(i)$
, so we skip the proof.
$(i)$
, so we skip the proof.
The following result provides a partial converse to the above theorem. Recall that a vertex
![]() $i\in Q_0$
is called a source (resp. a sink) of Q if there are no arrows
$i\in Q_0$
is called a source (resp. a sink) of Q if there are no arrows
![]() $\alpha \in Q_1$
such that
$\alpha \in Q_1$
such that
![]() $t(\alpha )=i$
(resp.
$t(\alpha )=i$
(resp.
![]() $s(\alpha )=i$
).
$s(\alpha )=i$
).
Theorem 8.3.2 Let
![]() $Q=(Q_0, Q_1)$
be a finite and acyclic quiver.
$Q=(Q_0, Q_1)$
be a finite and acyclic quiver.
-
(i) Let X be a silting object in
 $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. Then
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. Then
 $e_i(X)$
is a silting module in
$e_i(X)$
is a silting module in
 $\mathrm{Mod}\mbox {-}R$
, provided
$\mathrm{Mod}\mbox {-}R$
, provided
 $i\in Q_0$
is a source of Q.
$i\in Q_0$
is a source of Q. -
(ii) Let Y be a cosilting object in
 $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. Then
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. Then
 $e_i(Y)$
is a cosilting module in
$e_i(Y)$
is a cosilting module in
 $\mathrm{Mod}\mbox {-}R$
, provided
$\mathrm{Mod}\mbox {-}R$
, provided
 $i\in Q_0$
is a sink of Q.
$i\in Q_0$
is a sink of Q.
Proof.
![]() $(i)$
Since X is a silting object in
$(i)$
Since X is a silting object in
![]() $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
, there exists a projective presentation
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
, there exists a projective presentation
of X such that
![]() $\mathscr {D}_\sigma ={\mathrm {Gen}}(X)$
. By applying the exact functor
$\mathscr {D}_\sigma ={\mathrm {Gen}}(X)$
. By applying the exact functor
![]() $e_i$
on this exact sequence, we get the exact sequence
$e_i$
on this exact sequence, we get the exact sequence
which is a projective presentation of
![]() $e_i(X)=X_i$
.
$e_i(X)=X_i$
.
To complete the proof, we have to show that
![]() $\mathscr {D}_{\sigma _i}={\mathrm {Gen}}(X_i)$
. First, let
$\mathscr {D}_{\sigma _i}={\mathrm {Gen}}(X_i)$
. First, let
![]() $M\in \mathscr {D}_{\sigma _i}$
. Then there exists an epimorphism
$M\in \mathscr {D}_{\sigma _i}$
. Then there exists an epimorphism
By using the adjoint pair
![]() $(e_i, e_i^\rho )$
, we get the epimorphism
$(e_i, e_i^\rho )$
, we get the epimorphism
where
![]() $\mathscr {R}$
means
$\mathscr {R}$
means
![]() $\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. So
$\mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
. So
![]() $e_i^\rho (M)\in \mathscr {D}_\sigma ={\mathrm {Gen}}(X)$
. Therefore,
$e_i^\rho (M)\in \mathscr {D}_\sigma ={\mathrm {Gen}}(X)$
. Therefore,
![]() $M=e_i e_i^\rho (M)\in e_i({\mathrm {Gen}}(X))$
. But
$M=e_i e_i^\rho (M)\in e_i({\mathrm {Gen}}(X))$
. But
![]() $e_i({\mathrm {Gen}}(X))={\mathrm {Gen}}(e_i(X))={\mathrm {Gen}}(X_i)$
. Hence,
$e_i({\mathrm {Gen}}(X))={\mathrm {Gen}}(e_i(X))={\mathrm {Gen}}(X_i)$
. Hence,
![]() $\mathscr {D}_{\sigma _i}\subseteq {\mathrm {Gen}}(X_i)$
.
$\mathscr {D}_{\sigma _i}\subseteq {\mathrm {Gen}}(X_i)$
.
For the reverse inclusion, let
![]() $Y_i\in {\mathrm {Gen}}(X_i)$
. We define
$Y_i\in {\mathrm {Gen}}(X_i)$
. We define
![]() $Y\in \mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
by setting
$Y\in \mathrm {Rep}(Q, \mathrm{Mod}\mbox {-}R)$
by setting
![]() $Y_i$
at source vertex i, and
$Y_i$
at source vertex i, and
![]() $0$
elsewhere. Since i is a source, it follows easily that
$0$
elsewhere. Since i is a source, it follows easily that
![]() $Y \in {\mathrm {Gen}}(X)$
. Therefore,
$Y \in {\mathrm {Gen}}(X)$
. Therefore,
![]() $Y \in \mathscr {D}_\sigma $
, which implies that
$Y \in \mathscr {D}_\sigma $
, which implies that
![]() $Y_i \in \mathscr {D}_{\sigma _i}$
. Hence, we have the equality
$Y_i \in \mathscr {D}_{\sigma _i}$
. Hence, we have the equality
![]() $\mathscr {D}_{\sigma _i}={\mathrm {Gen}}(X_i)$
and the proof is complete.
$\mathscr {D}_{\sigma _i}={\mathrm {Gen}}(X_i)$
and the proof is complete.
![]() $(ii)$
The proof is just dual of the proof of part
$(ii)$
The proof is just dual of the proof of part
![]() $(i)$
. So we skip the proof.
$(i)$
. So we skip the proof.
Acknowledgements
The authors wish to thank the referee for the helpful comments and suggestions that have improved the paper. They also thank Bernhard Keller for pointing out Lemma 8.2.1 and Lidia Angeleri Hügel for the helpful discussions. This work was partly done during a visit of the authors to the Institut des Hautes Études Scientifiques (IHES), Paris, France. The authors would like to thank the support and excellent atmosphere at IHES.