Published online by Cambridge University Press: 07 August 2019
On établit une décomposition de l’homologie stable des groupes d’automorphismes des groupes libres à coefficients polynomiaux contravariants en termes d’homologie des foncteurs. Elle permet plusieurs calculs explicites, qui recoupent des résultats établis de manière indépendante par O. Randal-Williams et généralisent certains d’entre eux. Nos méthodes reposent sur l’examen d’extensions de Kan dérivées associées à plusieurs catégories de groupes libres, la généralisation d’un critère d’annulation homologique à coefficients polynomiaux dû à Scorichenko, le théorème de Galatius identifiant l’homologie stable des groupes d’automorphismes des groupes libres à celle des groupes symétriques, la machinerie des 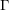 $\unicode[STIX]{x1D6E4}$-espaces et le scindement de Snaith.
$\unicode[STIX]{x1D6E4}$-espaces et le scindement de Snaith.
We establish a decomposition of stable homology of automorphism groups of free groups with polynomial contravariant coefficients in terms of functor homology. This allows several explicit computations, intersecting results obtained by independent methods by O. Randal-Williams and extending some of them. Our methods rely on the investigation of Kan extensions associated to several categories of free groups, the extension of a cancellation criterion for homology with polynomial coefficients due to Scorichenko, Galatius’s theorem identifying the stable homology of automorphism groups of free groups to that of symmetric groups, the machinery of 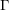 $\unicode[STIX]{x1D6E4}$-spaces and the Snaith splitting.
$\unicode[STIX]{x1D6E4}$-spaces and the Snaith splitting.