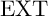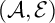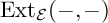1 Introduction
The Yoneda characterization of
![]() ${\operatorname{Ext}}$
is familiar to most students of homological algebra. Let
${\operatorname{Ext}}$
is familiar to most students of homological algebra. Let
![]() $A,B$
be two objects in an abelian category
$A,B$
be two objects in an abelian category
![]() $\cal{A}$
. Then
$\cal{A}$
. Then
![]() ${\operatorname{Ext}}_{\cal{A}}(A,B)$
is the set of all equivalence classes of sequences of the form
${\operatorname{Ext}}_{\cal{A}}(A,B)$
is the set of all equivalence classes of sequences of the form
![]() $0\to B\to C\to A\to 0$
, where two sequences
$0\to B\to C\to A\to 0$
, where two sequences
![]() $\alpha ,\beta $
are equivalent if we have the following commutative diagram:
$\alpha ,\beta $
are equivalent if we have the following commutative diagram:

Now,
![]() ${\operatorname{Ext}}_{\cal{A}}(A,B)$
can be given an abelian group structure by the well-known Baer sum as described in, for instance, [38, Tag 010I]. This consideration can be carried out more generally in any exact category (see [Reference Dräxler, Reiten, Smalø and Solberg14, §1.2]).
${\operatorname{Ext}}_{\cal{A}}(A,B)$
can be given an abelian group structure by the well-known Baer sum as described in, for instance, [38, Tag 010I]. This consideration can be carried out more generally in any exact category (see [Reference Dräxler, Reiten, Smalø and Solberg14, §1.2]).
The purpose of this note is to study the following rather natural questions: what if we place additional constraints on the short exact sequences? When do we get a subfunctor of
![]() ${\operatorname{Ext}}^1$
? Can one apply such functors to study ring and module theory, similar to the ways homological algebra has been very successfully applied in the last decades?
${\operatorname{Ext}}^1$
? Can one apply such functors to study ring and module theory, similar to the ways homological algebra has been very successfully applied in the last decades?
Let us elucidate our goals with a concrete example. Let
![]() $(R,\mathfrak {m},k)$
be a Noetherian local ring. Let
$(R,\mathfrak {m},k)$
be a Noetherian local ring. Let
![]() $A,B$
be finitely generated R-modules. We consider exact sequences
$A,B$
be finitely generated R-modules. We consider exact sequences
![]() $0\to B\to C\to A\to 0$
of R-modules, with the added condition that
$0\to B\to C\to A\to 0$
of R-modules, with the added condition that
![]() $\mu (C)=\mu (A)+\mu (B)$
, where
$\mu (C)=\mu (A)+\mu (B)$
, where
![]() $\mu (-)$
denotes the minimal number of generators. As we shall see later, the equivalence classes of such sequences do form a subfunctor of
$\mu (-)$
denotes the minimal number of generators. As we shall see later, the equivalence classes of such sequences do form a subfunctor of
![]() ${\operatorname{Ext}}^1_R$
, which we denote by
${\operatorname{Ext}}^1_R$
, which we denote by
![]() ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
. More surprisingly, the vanishing of a single module
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
. More surprisingly, the vanishing of a single module
![]() ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
can be used to characterize the regularity of R, a feature that is lacking with the classical
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
can be used to characterize the regularity of R, a feature that is lacking with the classical
![]() ${\operatorname{Ext}}^1$
.
${\operatorname{Ext}}^1$
.
Analogous versions of classical homological functors have been studied by various authors, notably starting with Hochschild [Reference Hochschild23] who studied relative
![]() ${\operatorname{Ext}}$
and
${\operatorname{Ext}}$
and
![]() $\operatorname{Tor}$
groups of modules over a ring with respect to subrings of the original ring. This work is further developed by Butler–Horrocks as well as Auslander–Solberg, where the point of view is switched to allowable exact sequences that give rise to sub(bi)functors of
$\operatorname{Tor}$
groups of modules over a ring with respect to subrings of the original ring. This work is further developed by Butler–Horrocks as well as Auslander–Solberg, where the point of view is switched to allowable exact sequences that give rise to sub(bi)functors of
![]() ${\operatorname{Ext}}^1$
. The whole circle of ideas is now thriving on its own under the name relative homological algebra, with exact structures playing a fundamental role (see [Reference Brüstle, Hassoun, Langford and Roy4], [Reference Buan5], [Reference Crivei8], [Reference Dräxler, Reiten, Smalø and Solberg14], [Reference Enochs and Jenda16]–[Reference Enomoto18], [Reference Matsui28], [Reference Rump33], [Reference Zhu and Zhuang40]] for an incomplete list of literature and [Reference Bühler6], [Reference Solberg34] for some excellent surveys). In commutative algebra, as far as we know, this line of inquiry has not been exploited thoroughly; however, traces of it can be found in [Reference Puthenpurakal31], [Reference Striuli35], and [Reference Eisenbud and Schreyer15, §§1 and 2].
${\operatorname{Ext}}^1$
. The whole circle of ideas is now thriving on its own under the name relative homological algebra, with exact structures playing a fundamental role (see [Reference Brüstle, Hassoun, Langford and Roy4], [Reference Buan5], [Reference Crivei8], [Reference Dräxler, Reiten, Smalø and Solberg14], [Reference Enochs and Jenda16]–[Reference Enomoto18], [Reference Matsui28], [Reference Rump33], [Reference Zhu and Zhuang40]] for an incomplete list of literature and [Reference Bühler6], [Reference Solberg34] for some excellent surveys). In commutative algebra, as far as we know, this line of inquiry has not been exploited thoroughly; however, traces of it can be found in [Reference Puthenpurakal31], [Reference Striuli35], and [Reference Eisenbud and Schreyer15, §§1 and 2].
Although the existing literature provides excellent starting points and inspiring ideas for this present work, it is not always easy to extract the precise results needed for our intended applications. For instance, while the connections between subfunctors of
![]() ${\operatorname{Ext}}^1$
and certain sub-exact structures on a fixed category are well known [Reference Dräxler, Reiten, Smalø and Solberg14, §1.2], checking the conditions of substructures in each case can be time-consuming.
${\operatorname{Ext}}^1$
and certain sub-exact structures on a fixed category are well known [Reference Dräxler, Reiten, Smalø and Solberg14, §1.2], checking the conditions of substructures in each case can be time-consuming.
We are able to find criteria that can be applied in broad settings to identify exact subcategories and subfunctors. Here is a sample result applicable to our motivating example above, which follows from Theorem 4.8 and Proposition 3.8.
Theorem 1.1. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\phi :{\cal{A}} \to \mathbb Z$
be a function such that
$\phi :{\cal{A}} \to \mathbb Z$
be a function such that
![]() $\phi $
is constant on isomorphism classes of objects in
$\phi $
is constant on isomorphism classes of objects in
![]() $\cal{A}$
,
$\cal{A}$
,
![]() $\phi $
is additive on finite biproducts, and
$\phi $
is additive on finite biproducts, and
![]() $\phi $
is sub-additive on kernel–cokernel pairs in
$\phi $
is sub-additive on kernel–cokernel pairs in
![]() $\cal{E}$
(i.e., if
$\cal{E}$
(i.e., if
![]() is in
is in
![]() $\cal{E}$
, then
$\cal{E}$
, then
![]() $\phi (N)\le \phi (M)+\phi (L)$
). Set
$\phi (N)\le \phi (M)+\phi (L)$
). Set
![]() ${\cal{E}}^{\phi }:=\{\text {kernel--cokernel pairs in } {\cal{E}} \text { on which } \phi \text { is additive} \}$
. Then
${\cal{E}}^{\phi }:=\{\text {kernel--cokernel pairs in } {\cal{E}} \text { on which } \phi \text { is additive} \}$
. Then
![]() ${\cal{E}}^{\phi }$
gives rise, via the Yoneda construction, to a subfunctor of
${\cal{E}}^{\phi }$
gives rise, via the Yoneda construction, to a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)$
.
${\operatorname{Ext}}_{\cal{E}}(-,-)$
.
Our above theorem is partly motivated by, and can be used to recover and extend, recent interesting work of Puthenpurakal in [Reference Puthenpurakal31] (see Theorem 4.17).
Another situation we would like to have convenient criteria for subfunctors is when one restricts to a certain subcategory. A concrete example we have in mind concerns Ulrich modules and their recent generalizations. These modules form a subcategory of Cohen–Macaulay modules over a commutative ring and have been receiving increasing attention over the years due to very interesting and useful algebraic and geometric properties that their existence or abundance imply. We are able to show that even the generalized notion of I-Ulrich modules, recently introduced in [Reference Dao, Maitra and Sridhar11], induces subfunctors of
![]() ${\operatorname{Ext}}^1_R(-,-)$
. See Proposition 4.1 and Corollary 4.7 in this regard.
${\operatorname{Ext}}^1_R(-,-)$
. See Proposition 4.1 and Corollary 4.7 in this regard.
While this work is mainly concerned with foundational results, we also study the properties of some chosen new subfunctors, just to see if they are worth our efforts to show their existence! The early returns seem promising: these functors can be used to detect a wide range of ring and module-theoretic properties. Below we shall describe the organization of the paper and describe the most interesting findings in more detail.
Section 2 is devoted to preliminary results on subfunctors of additive functors. While these results are perhaps not new, we were unable to locate convenient references, hence their inclusion.
Section 3 establishes various foundational results on exact subcategories, which form the cornerstone of the theory. As mentioned above, our applications require some extra care in preparation, and we try to give complete proofs whenever possible.
Section 4 concerns our first main application. We study sub-additive numerical functions
![]() $\phi $
on an exact category and show that under mild conditions they induce exact subcategories and hence subfunctors of
$\phi $
on an exact category and show that under mild conditions they induce exact subcategories and hence subfunctors of
![]() ${\operatorname{Ext}}^1(-,-)$
, which we denote by
${\operatorname{Ext}}^1(-,-)$
, which we denote by
![]() ${\operatorname{Ext}}^1(-,-)^{\phi }$
. See Theorem 4.8. A key consequence, Theorem 4.17, is inspired by, as well as extends, [Reference Puthenpurakal31, Ths. 3.11 and 3.13]. We also give similar results about subfunctors of
${\operatorname{Ext}}^1(-,-)^{\phi }$
. See Theorem 4.8. A key consequence, Theorem 4.17, is inspired by, as well as extends, [Reference Puthenpurakal31, Ths. 3.11 and 3.13]. We also give similar results about subfunctors of
![]() ${\operatorname{Ext}}^1$
induced by half-exact functors, in the spirit of [Reference Auslander and Solberg1] (see Corollaries 4.13 and 4.14).
${\operatorname{Ext}}^1$
induced by half-exact functors, in the spirit of [Reference Auslander and Solberg1] (see Corollaries 4.13 and 4.14).
In §5, we focus on two special types of subfunctors, which arise from simple applications of previous sections. Already these cases appear to be interesting and useful. The first one is
![]() ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
, where
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
, where
![]() $\mu $
is the minimal number of generators function mentioned above. We compute the values of this subfunctor on all (pair of) finitely generated modules over a discrete valuation ring, i.e., DVR (Corollary 5.1.14), as well as for certain pairs of modules over a Cohen–Macaulay ring of minimal multiplicity (Proposition 5.1.22).
$\mu $
is the minimal number of generators function mentioned above. We compute the values of this subfunctor on all (pair of) finitely generated modules over a discrete valuation ring, i.e., DVR (Corollary 5.1.14), as well as for certain pairs of modules over a Cohen–Macaulay ring of minimal multiplicity (Proposition 5.1.22).
Using this subfunctor, we prove the following characterization of the regularity of local rings, which is the combination of Theorems 5.1.1 and 5.1.12, Proposition 5.1.14, and Corollary 5.2.7. Note that the regularity can be detected by the vanishing of a single
![]() ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
-module. In the following statement, we mention that for a finitely generated module M over the local ring R,
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
-module. In the following statement, we mention that for a finitely generated module M over the local ring R,
![]() $\Omega ^i_R M$
denotes the ith syzygy in a minimal free resolution of M.
$\Omega ^i_R M$
denotes the ith syzygy in a minimal free resolution of M.
Theorem 1.2. Let
![]() $(R,\mathfrak {m},k)$
be a local ring of depth
$(R,\mathfrak {m},k)$
be a local ring of depth
![]() $t>0$
. Then, the following are equivalent:
$t>0$
. Then, the following are equivalent:
-
(1) R is regular.
-
(2)
 ${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)^{\mu }=0$
for some R-regular sequence
${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)^{\mu }=0$
for some R-regular sequence
 $x_1,...,x_{t-1}$
.
$x_1,...,x_{t-1}$
. -
(3)
 ${\operatorname{Ext}}^1_R(k,M)^{\mu }=0$
for some finitely generated R-module M of projective dimension
${\operatorname{Ext}}^1_R(k,M)^{\mu }=0$
for some finitely generated R-module M of projective dimension
 $t-1$
.
$t-1$
. -
(4) R is Cohen–Macaulay, and
 ${\operatorname{Ext}}^1_R(\Omega ^{t-1}_R k,N)^{\mu }=0$
for some finitely generated nonzero R-module N of finite injective dimension.
${\operatorname{Ext}}^1_R(\Omega ^{t-1}_R k,N)^{\mu }=0$
for some finitely generated nonzero R-module N of finite injective dimension.Moreover, if
 $t=1$
, then the above are also equivalent to each of the following.
$t=1$
, then the above are also equivalent to each of the following. -
(5)
 ${\operatorname{Ext}}^1_R(M,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
for all finitely generated R-modules M and N.
${\operatorname{Ext}}^1_R(M,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
for all finitely generated R-modules M and N. -
(6) R is Cohen–Macaulay, and there exist Ulrich modules
 $M,N$
such that N is faithful,
$M,N$
such that N is faithful,
 $M\ne 0$
, and for every R-module X that fits into a short exact sequence
$M\ne 0$
, and for every R-module X that fits into a short exact sequence
 $0\to N\to X\to M \to 0 $
, one has X is also an Ulrich module.
$0\to N\to X\to M \to 0 $
, one has X is also an Ulrich module.
We note here that the usual
![]() ${\operatorname{Ext}}$
-modules (without the
${\operatorname{Ext}}$
-modules (without the
![]() $\mu $
) in (2)–(4) of the above theorem are always nonzero. Moreover, the statement of part (6) of Theorem 1.2 apparently has nothing to do with subfunctor of
$\mu $
) in (2)–(4) of the above theorem are always nonzero. Moreover, the statement of part (6) of Theorem 1.2 apparently has nothing to do with subfunctor of
![]() ${\operatorname{Ext}}^1$
, but we do not know a proof of
${\operatorname{Ext}}^1$
, but we do not know a proof of
![]() $(1)\iff (6)$
(which is contained in Corollary 5.2.7) without resorting to
$(1)\iff (6)$
(which is contained in Corollary 5.2.7) without resorting to
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(-,-): \operatorname{Ul}(R)^{op}\times \operatorname{Ul}(R)\to {\operatorname{mod}}\ R$
.
${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(-,-): \operatorname{Ul}(R)^{op}\times \operatorname{Ul}(R)\to {\operatorname{mod}}\ R$
.
It is worth mentioning that one can also use
![]() ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
to detect the property of R being a hypersurface of minimal multiplicity (Corollary 5.1.23) or the weak
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
to detect the property of R being a hypersurface of minimal multiplicity (Corollary 5.1.23) or the weak
![]() $\mathfrak {m}$
-fullness of a submodule (Proposition 5.1.11).
$\mathfrak {m}$
-fullness of a submodule (Proposition 5.1.11).
The second type arises from I-Ulrich modules, where I is any
![]() $\mathfrak {m}$
-primary ideal in a Noetherian local ring
$\mathfrak {m}$
-primary ideal in a Noetherian local ring
![]() $(R,\mathfrak {m})$
. See Definition 4.5 and Corollary 4.7 for the definition of I-Ulrich modules and the fact that they form an exact category. In Theorem 5.2.14, using a subfunctor of
$(R,\mathfrak {m})$
. See Definition 4.5 and Corollary 4.7 for the definition of I-Ulrich modules and the fact that they form an exact category. In Theorem 5.2.14, using a subfunctor of
![]() ${\operatorname{Ext}}^1$
corresponding to Ulrich modules over one-dimensional local Cohen–Macaulay rings, we give some characterizations of modules belonging to
${\operatorname{Ext}}^1$
corresponding to Ulrich modules over one-dimensional local Cohen–Macaulay rings, we give some characterizations of modules belonging to
![]() $\operatorname{add}_R(B(\mathfrak {m}))$
and also characterize when
$\operatorname{add}_R(B(\mathfrak {m}))$
and also characterize when
![]() $B(\mathfrak {m})$
is a Gorenstein ring in terms of annihilator of
$B(\mathfrak {m})$
is a Gorenstein ring in terms of annihilator of
![]() ${\operatorname{Ext}}^1_R$
of Ulrich modules. Here,
${\operatorname{Ext}}^1_R$
of Ulrich modules. Here,
![]() $B(-)$
denotes the blow-up. We give some applications of Theorem 5.2.14, one of which relates annihilation of
$B(-)$
denotes the blow-up. We give some applications of Theorem 5.2.14, one of which relates annihilation of
![]() ${\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})$
with that of
${\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})$
with that of
![]() ${\operatorname{Ext}}^1_R\left (\operatorname{Ul}_{\omega }(R),B(\omega )\right )$
(see Corollary 5.2.17).
${\operatorname{Ext}}^1_R\left (\operatorname{Ul}_{\omega }(R),B(\omega )\right )$
(see Corollary 5.2.17).
Finally, we should mention that one of the main applications of our results has appeared in a separate work, where we study the splitting of short exact sequences of Ulrich modules and connections to other properties of singularities (see [Reference Dao, Dey and Dutta9]).
2 Preliminaries on subfunctors of additive functors
Unless otherwise stated, all rings in this paper are assumed to be commutative, Noetherian, and with unity. For a ring R,
![]() $Q(R)$
will denote its total ring of fractions. For an R-module M,
$Q(R)$
will denote its total ring of fractions. For an R-module M,
![]() $\lambda _R(M)$
will denote its length. For a finitely generated R-module M, and
$\lambda _R(M)$
will denote its length. For a finitely generated R-module M, and
![]() $i\geq 1$
, by
$i\geq 1$
, by
![]() $\Omega ^i_R M$
we mean
$\Omega ^i_R M$
we mean
![]() $\text {Im} f_{i}$
, where we have an exact sequence
$\text {Im} f_{i}$
, where we have an exact sequence
![]() $F_{i}\xrightarrow {f_{i}} F_{i-1}\xrightarrow {f_{i-1}}\cdots \to F_0\to M \to 0$
, with each
$F_{i}\xrightarrow {f_{i}} F_{i-1}\xrightarrow {f_{i-1}}\cdots \to F_0\to M \to 0$
, with each
![]() $F_j$
being a finitely generated projective R-module. When R is moreover local, we choose this so that
$F_j$
being a finitely generated projective R-module. When R is moreover local, we choose this so that
![]() $\text {Im}(f_j)\subseteq \mathfrak {m} F_{j-1}$
for each j (see [Reference Bruns and Herzog3, Prop. 1.3.1]).
$\text {Im}(f_j)\subseteq \mathfrak {m} F_{j-1}$
for each j (see [Reference Bruns and Herzog3, Prop. 1.3.1]).
For definitions, and basic properties of additive categories, additive functors, R-linear categories, and R-linear functors, we refer the reader to [38, Tags 09SE, 010M, and 09MI]. We now recall the definition of subfunctors as in [29].
Definition 2.1. Let
![]() ${\cal{A}},{\cal{B}}$
be two categories. Let
${\cal{A}},{\cal{B}}$
be two categories. Let
![]() $F: {\cal{A}} \to {\cal{B}}$
be a covariant (resp. contravariant) functor. A covariant (resp. contravariant) functor
$F: {\cal{A}} \to {\cal{B}}$
be a covariant (resp. contravariant) functor. A covariant (resp. contravariant) functor
![]() $G: {\cal{A}} \to {\cal{B}}$
is called a subfunctor of F if for every
$G: {\cal{A}} \to {\cal{B}}$
is called a subfunctor of F if for every
![]() $M\in {\cal{A}}$
, there exists a monomorphism
$M\in {\cal{A}}$
, there exists a monomorphism
![]() $j_M:G(M)\to F(M)$
, and moreover, for every
$j_M:G(M)\to F(M)$
, and moreover, for every
![]() $M,N\in {\cal{A}}$
, and
$M,N\in {\cal{A}}$
, and
![]() $f\in \operatorname{Mor}_{\cal{A}}(M,N)$
, the following diagrams are commutative, where the left one stands for the covariant case and the right one for the contravariant case:
$f\in \operatorname{Mor}_{\cal{A}}(M,N)$
, the following diagrams are commutative, where the left one stands for the covariant case and the right one for the contravariant case:

2.2. For our purposes, we will always take
![]() $\cal{B}$
to be either the category of abelian groups
$\cal{B}$
to be either the category of abelian groups
![]() $\mathbf {Ab}$
,
$\mathbf {Ab}$
,
![]() ${\operatorname{Mod}}\ R$
or
${\operatorname{Mod}}\ R$
or
![]() ${\operatorname{mod}}\ R$
(hence monomorphisms are just injective morphisms) for some commutative ring R, and
${\operatorname{mod}}\ R$
(hence monomorphisms are just injective morphisms) for some commutative ring R, and
![]() $j_M$
will usually be just the inclusion map.
$j_M$
will usually be just the inclusion map.
The following lemma is probably well known, but we could not find an appropriate reference; hence, we include a proof. This will be used throughout the remainder of the article, possibly without further reference.
Lemma 2.3.
-
(1) Subfunctor of an additive functor, between two additive categories, is additive.
-
(2) Subfunctor of an R-linear functor, between two R-linear categories, is R-linear.
Proof. We will only prove the covariant case of both, since the contravariant case is similar.
(1) Let
![]() ${\cal{A}},{\cal{B}}$
be two additive categories, and let
${\cal{A}},{\cal{B}}$
be two additive categories, and let
![]() $F:{\cal{A}}\to {\cal{B}}$
be an additive functor. Also, let
$F:{\cal{A}}\to {\cal{B}}$
be an additive functor. Also, let
![]() $G: {\cal{A}} \to {\cal{B}}$
be a subfunctor of F. Then we have to show that the map
$G: {\cal{A}} \to {\cal{B}}$
be a subfunctor of F. Then we have to show that the map
![]() $G:\operatorname{Mor}_{\cal{A}}(X,Y)\to \operatorname{Mor}_{\cal{B}}(G(X),G(Y))$
is a homomorphism of abelian groups for all
$G:\operatorname{Mor}_{\cal{A}}(X,Y)\to \operatorname{Mor}_{\cal{B}}(G(X),G(Y))$
is a homomorphism of abelian groups for all
![]() $X,Y\in {\cal{A}}$
. Fix two objects
$X,Y\in {\cal{A}}$
. Fix two objects
![]() $X,Y\in {\cal{A}}$
. Then we need to prove that
$X,Y\in {\cal{A}}$
. Then we need to prove that
![]() $G(f+g)=G(f)+G(g)$
for all
$G(f+g)=G(f)+G(g)$
for all
![]() $f,g\in \operatorname{Mor}_{\cal{A}}(X,Y)$
. Since G is a subfunctor of F, we have the following commutative diagrams:
$f,g\in \operatorname{Mor}_{\cal{A}}(X,Y)$
. Since G is a subfunctor of F, we have the following commutative diagrams:

Then we get
 $$ \begin{align*} j_Y\circ G(f+g) &=F(f+g)\circ j_X\\ &= (F(f)+F(g))\circ j_X\text{ [Since }F\text{ is additive]}\\ &=F(f)\circ j_X+F(g)\circ j_X\\ &=j_Y\circ G(f)+j_Y\circ G(g)\\ &=j_Y\circ (G(f)+G(g)), \end{align*} $$
$$ \begin{align*} j_Y\circ G(f+g) &=F(f+g)\circ j_X\\ &= (F(f)+F(g))\circ j_X\text{ [Since }F\text{ is additive]}\\ &=F(f)\circ j_X+F(g)\circ j_X\\ &=j_Y\circ G(f)+j_Y\circ G(g)\\ &=j_Y\circ (G(f)+G(g)), \end{align*} $$
where the third and fifth equalities follow from the fact that
![]() $\cal{B}$
is an additive category. Now, since
$\cal{B}$
is an additive category. Now, since
![]() $j_Y$
is a monomorphism, so
$j_Y$
is a monomorphism, so
![]() $j_Y\circ G(f+g)=j_Y\circ (G(f)+G(g))$
implies that
$j_Y\circ G(f+g)=j_Y\circ (G(f)+G(g))$
implies that
![]() $G(f+g)=G(f)+G(g)$
. Hence, G is additive.
$G(f+g)=G(f)+G(g)$
. Hence, G is additive.
(2) Let
![]() ${\cal{A}},{\cal{B}}$
be two R-linear categories, and let
${\cal{A}},{\cal{B}}$
be two R-linear categories, and let
![]() $F:{\cal{A}}\to {\cal{B}}$
be an R-linear functor. Also, let
$F:{\cal{A}}\to {\cal{B}}$
be an R-linear functor. Also, let
![]() $G: {\cal{A}} \to {\cal{B}}$
be a subfunctor of F. Then we have to show that the map
$G: {\cal{A}} \to {\cal{B}}$
be a subfunctor of F. Then we have to show that the map
![]() $G:\operatorname{Mor}_{\cal{A}}(X,Y)\to \operatorname{Mor}_{\cal{B}}(G(X),G(Y))$
is an R-linear map for all
$G:\operatorname{Mor}_{\cal{A}}(X,Y)\to \operatorname{Mor}_{\cal{B}}(G(X),G(Y))$
is an R-linear map for all
![]() $X,Y\in {\cal{A}}$
. Fix two objects
$X,Y\in {\cal{A}}$
. Fix two objects
![]() $X, Y\in {\cal{A}}$
. Then, by part (1), we already have the additivity of G, so we only need to prove that
$X, Y\in {\cal{A}}$
. Then, by part (1), we already have the additivity of G, so we only need to prove that
![]() $G(rf)=rG(f)$
for all
$G(rf)=rG(f)$
for all
![]() $f\in \operatorname{Mor}_{\cal{A}}(X,Y)$
and for all
$f\in \operatorname{Mor}_{\cal{A}}(X,Y)$
and for all
![]() $r\in R$
. Since G is a subfunctor of F, we have the following commutative diagrams:
$r\in R$
. Since G is a subfunctor of F, we have the following commutative diagrams:

Then we get
 $$ \begin{align*} j_Y\circ G(rf) &=F(rf)\circ j_X\\ &= (rF(f))\circ j_X\text{ [Since }F\text{ is }R\text{-linear]}\\ &=r(F(f)\circ j_X)\\ &=r(j_Y\circ G(f))\\ &=j_Y\circ (rG(f)), \end{align*} $$
$$ \begin{align*} j_Y\circ G(rf) &=F(rf)\circ j_X\\ &= (rF(f))\circ j_X\text{ [Since }F\text{ is }R\text{-linear]}\\ &=r(F(f)\circ j_X)\\ &=r(j_Y\circ G(f))\\ &=j_Y\circ (rG(f)), \end{align*} $$
where the third and fifth equalities follow from the fact that
![]() $\cal{B}$
is an R-linear category. Now, since
$\cal{B}$
is an R-linear category. Now, since
![]() $j_Y$
is a monomorphism, so
$j_Y$
is a monomorphism, so
![]() $j_Y\circ G(rf)=j_Y\circ (rG(f))$
implies that
$j_Y\circ G(rf)=j_Y\circ (rG(f))$
implies that
![]() $G(rf)=rG(f)$
. Hence, G is R-linear.
$G(rf)=rG(f)$
. Hence, G is R-linear.
We finish this section with a submodule inclusion result relating subfunctors of R-linear functors which will be applied in §5.
Lemma 2.4. Let
![]() $\cal{A}$
be an additive R-linear category, and let
$\cal{A}$
be an additive R-linear category, and let
![]() $G:{\cal{A}}\to {\operatorname{mod}}\ R$
be a subfunctor of an R-linear functor
$G:{\cal{A}}\to {\operatorname{mod}}\ R$
be a subfunctor of an R-linear functor
![]() $F:{\cal{A}} \to {\operatorname{Mod}}\ R$
, and for every object
$F:{\cal{A}} \to {\operatorname{Mod}}\ R$
, and for every object
![]() $A\in {\cal{A}}$
, let
$A\in {\cal{A}}$
, let
![]() $j_A:G(A)\to F(A)$
be the monomorphism as in the definition of a subfunctor. Let I be an ideal of R. Let
$j_A:G(A)\to F(A)$
be the monomorphism as in the definition of a subfunctor. Let I be an ideal of R. Let
![]() $\{A_i\}_{i=1}^n$
be objects in
$\{A_i\}_{i=1}^n$
be objects in
![]() $\cal{A}$
such that
$\cal{A}$
such that
![]() $j_{A_i}\left (G(A_i)\right )\subseteq IF(A_i)$
(resp.
$j_{A_i}\left (G(A_i)\right )\subseteq IF(A_i)$
(resp.
![]() $j_{A_i}\left (G(A_i)\right )\supseteq IF(A_i)$
) for all
$j_{A_i}\left (G(A_i)\right )\supseteq IF(A_i)$
) for all
![]() $i=1,...,n$
. Let
$i=1,...,n$
. Let
![]() $X:=\oplus _{i=1}^nA_i$
. Then, it holds that
$X:=\oplus _{i=1}^nA_i$
. Then, it holds that
![]() $j_{X} \left (G(X)\right )\subseteq IF(X)$
(resp.
$j_{X} \left (G(X)\right )\subseteq IF(X)$
(resp.
![]() $j_{X} \left (G(X)\right )\supseteq IF(X)$
).
$j_{X} \left (G(X)\right )\supseteq IF(X)$
).
Proof. We will only do the covariant case, the contravariant case being similar. For every i, we have
![]() $\pi _i:X \to A_i$
, which gives rise to the following commutative diagram:
$\pi _i:X \to A_i$
, which gives rise to the following commutative diagram:

Consequently, we get the following commutative diagram:

where the horizontal arrows are isomorphisms, since F and consequently G are additive functors (see Lemma 2.3). Call the top horizontal map
![]() $\theta $
, and the bottom one
$\theta $
, and the bottom one
![]() $\alpha $
, so that
$\alpha $
, so that
![]() $\alpha \circ j_X=(\oplus _{i=1}^nj_{A_i})\circ \theta $
; hence,
$\alpha \circ j_X=(\oplus _{i=1}^nj_{A_i})\circ \theta $
; hence,
![]() $j_X\circ \theta ^{-1}=\alpha ^{-1}\circ (\oplus _{i=1}^nj_{A_i})$
. So, now, we get
$j_X\circ \theta ^{-1}=\alpha ^{-1}\circ (\oplus _{i=1}^nj_{A_i})$
. So, now, we get
 $$ \begin{align*} j_X(G(X))=(j_X \circ \theta^{-1}) (\theta(G(X)))=(j_X\circ \theta^{-1})(\oplus_{i=1}^nG(A_i)) &=(\alpha^{-1}\circ (\oplus_{i=1}^nj_{A_i}\kern-1pt))(\oplus_{i=1}^nG(A_i)\kern-1pt)\\ &=\alpha^{-1}(\oplus_{i=1}^n j_{A_i}(G(A_i))). \end{align*} $$
$$ \begin{align*} j_X(G(X))=(j_X \circ \theta^{-1}) (\theta(G(X)))=(j_X\circ \theta^{-1})(\oplus_{i=1}^nG(A_i)) &=(\alpha^{-1}\circ (\oplus_{i=1}^nj_{A_i}\kern-1pt))(\oplus_{i=1}^nG(A_i)\kern-1pt)\\ &=\alpha^{-1}(\oplus_{i=1}^n j_{A_i}(G(A_i))). \end{align*} $$
So, if
![]() $j_{A_i}\left (G(A_i)\right )\subseteq IF(A_i)$
(resp.
$j_{A_i}\left (G(A_i)\right )\subseteq IF(A_i)$
(resp.
![]() $j_{A_i}\left (G(A_i)\right )\supseteq IF(A_i)$
) for all
$j_{A_i}\left (G(A_i)\right )\supseteq IF(A_i)$
) for all
![]() $i=1,...,n$
, then
$i=1,...,n$
, then
(resp.
![]() $j_X(G(X))\supseteq \alpha ^{-1}(\oplus _{i=1}^n IF(A_i))=\alpha ^{-1}(I\left (\oplus _{i=1}^n F(A_i)\right ))=I\alpha ^{-1}(\oplus _{i=1}^n F(A_i))=IF(X)$
),
$j_X(G(X))\supseteq \alpha ^{-1}(\oplus _{i=1}^n IF(A_i))=\alpha ^{-1}(I\left (\oplus _{i=1}^n F(A_i)\right ))=I\alpha ^{-1}(\oplus _{i=1}^n F(A_i))=IF(X)$
),
where we have used
![]() $\alpha ^{-1}(IM)=I\alpha ^{-1}(M)$
, since
$\alpha ^{-1}(IM)=I\alpha ^{-1}(M)$
, since
![]() $\alpha $
is an R-linear map.
$\alpha $
is an R-linear map.
3 Some generalities about exact subcategories
In this section, we record some generalities about exact subcategories of an exact category that we will later use for subcategories of
![]() ${\operatorname{mod}}\ R$
when R is a commutative Noetherian ring. All our subcategories are strict (closed under isomorphism classes) and full, and we often abbreviate this as strictly full. We will follow the definition of an exact category described in [Reference Bühler6, Def. 2.1]. We try to provide complete proofs whenever possible.
${\operatorname{mod}}\ R$
when R is a commutative Noetherian ring. All our subcategories are strict (closed under isomorphism classes) and full, and we often abbreviate this as strictly full. We will follow the definition of an exact category described in [Reference Bühler6, Def. 2.1]. We try to provide complete proofs whenever possible.
Given an exact category
![]() $({\cal{A}},{\cal{E}})$
, we call a monomorphism
$({\cal{A}},{\cal{E}})$
, we call a monomorphism
![]() $X\xrightarrow {i} Y$
to be an
$X\xrightarrow {i} Y$
to be an
![]() $\cal{E}$
-inflation (also, called an admissible monic) if it is the part of a kernel–cokernel pair
$\cal{E}$
-inflation (also, called an admissible monic) if it is the part of a kernel–cokernel pair
![]() $X\xrightarrow {i} Y\xrightarrow {} Z$
, which lies in
$X\xrightarrow {i} Y\xrightarrow {} Z$
, which lies in
![]() $\cal{E}$
. Dually, we call an epimorphism
$\cal{E}$
. Dually, we call an epimorphism
![]() $Y\xrightarrow {p} Z$
to be an
$Y\xrightarrow {p} Z$
to be an
![]() $\cal{E}$
-deflation (also, called an admissible epic) if it is the part of a kernel–cokernel pair
$\cal{E}$
-deflation (also, called an admissible epic) if it is the part of a kernel–cokernel pair
![]() $X\xrightarrow {} Y\xrightarrow {p} Z$
, which lies in
$X\xrightarrow {} Y\xrightarrow {p} Z$
, which lies in
![]() $\cal{E}$
. We will often denote an admissible monic (resp. an admissible epic) by
$\cal{E}$
. We will often denote an admissible monic (resp. an admissible epic) by
![]() (resp.
(resp.
![]() ).
).
We begin by stating a lemma on morphisms and kernel–cokernel pairs, which we will use frequently while proving that certain structures are closed under isomorphism classes of kernel–cokernel pairs. This should be standard and well known, but we could not find an appropriate reference; hence, we include a proof.
Lemma 3.1. Let
![]() $\cal{A}$
be an additive category. Let
$\cal{A}$
be an additive category. Let
![]() $M,N,L\in {\cal{A}}$
be such that
$M,N,L\in {\cal{A}}$
be such that
![]() $M\xrightarrow {i} N\xrightarrow {d} L$
is a kernel–cokernel pair in
$M\xrightarrow {i} N\xrightarrow {d} L$
is a kernel–cokernel pair in
![]() $\cal{A}$
. Also, let
$\cal{A}$
. Also, let
![]() $M',N',L'\in {\cal{A}}$
. Consider morphisms
$M',N',L'\in {\cal{A}}$
. Consider morphisms
![]() $M'\xrightarrow {i'} N'$
,
$M'\xrightarrow {i'} N'$
,
![]() $N'\xrightarrow {d'} L'$
. If we have the following diagram with commutative squares:
$N'\xrightarrow {d'} L'$
. If we have the following diagram with commutative squares:

where the vertical arrows
![]() $\phi _1,\phi _2,\phi _3$
are isomorphisms, then
$\phi _1,\phi _2,\phi _3$
are isomorphisms, then
![]() $M'\xrightarrow {i'} N'\xrightarrow {d'} L'$
is a kernel–cokernel pair in
$M'\xrightarrow {i'} N'\xrightarrow {d'} L'$
is a kernel–cokernel pair in
![]() $\cal{A}$
.
$\cal{A}$
.
Proof. We will only prove that
![]() $\ker (d')=i'$
, since the proof of
$\ker (d')=i'$
, since the proof of
![]() $\operatorname{Coker}(i')=d'$
can be given by a dual argument. From the above commutative diagram, we have
$\operatorname{Coker}(i')=d'$
can be given by a dual argument. From the above commutative diagram, we have
Since
![]() $M\xrightarrow {i} N\xrightarrow {d} L$
is a kernel–cokernel pair in
$M\xrightarrow {i} N\xrightarrow {d} L$
is a kernel–cokernel pair in
![]() $\cal{A}$
, we get
$\cal{A}$
, we get
![]() $d\circ i=0$
. Then, by Equation (3.1), we have
$d\circ i=0$
. Then, by Equation (3.1), we have
![]() $d'\circ i'=(\phi _3\circ d\circ \phi _2^{-1})\circ (\phi _2\circ i\circ \phi _1^{-1})=\phi _3\circ d\circ i\circ \phi _1^{-1}=\phi _3\circ 0\circ \phi _1^{-1}=0$
. Now, let
$d'\circ i'=(\phi _3\circ d\circ \phi _2^{-1})\circ (\phi _2\circ i\circ \phi _1^{-1})=\phi _3\circ d\circ i\circ \phi _1^{-1}=\phi _3\circ 0\circ \phi _1^{-1}=0$
. Now, let
![]() $K\in {\cal{A}}$
and consider a morphism
$K\in {\cal{A}}$
and consider a morphism
![]() $f':K\to N'$
such that
$f':K\to N'$
such that
![]() $d'\circ f'=0$
. Define
$d'\circ f'=0$
. Define
![]() $f:=\phi _2^{-1}\circ f':K\to N$
. Then, by Equation (3.1), we get that
$f:=\phi _2^{-1}\circ f':K\to N$
. Then, by Equation (3.1), we get that
![]() $d\circ f=d\circ (\phi _2^{-1}\circ f')=(d\circ \phi _2^{-1})\circ f'=(\phi _3^{-1}\circ d')\circ f'=\phi _3^{-1}\circ (d'\circ f')=\phi _3^{-1}\circ 0=0$
. Now, since
$d\circ f=d\circ (\phi _2^{-1}\circ f')=(d\circ \phi _2^{-1})\circ f'=(\phi _3^{-1}\circ d')\circ f'=\phi _3^{-1}\circ (d'\circ f')=\phi _3^{-1}\circ 0=0$
. Now, since
![]() $\ker (d)=i$
, by the universal property of a kernel of a map, there exists a morphism
$\ker (d)=i$
, by the universal property of a kernel of a map, there exists a morphism
![]() $u:K\to M$
such that
$u:K\to M$
such that
![]() $i\circ u=f$
. Now, define
$i\circ u=f$
. Now, define
![]() $u':=\phi _1\circ u:K\to M'$
. Then, by Equation (3.1), we get that
$u':=\phi _1\circ u:K\to M'$
. Then, by Equation (3.1), we get that
![]() $i'\circ u'=i'\circ (\phi _1\circ u)=(i'\circ \phi _1)\circ u=(\phi _2\circ i)\circ u=\phi _2\circ f=\phi _2\circ (\phi _2^{-1}\circ f')=f'$
. This implies that
$i'\circ u'=i'\circ (\phi _1\circ u)=(i'\circ \phi _1)\circ u=(\phi _2\circ i)\circ u=\phi _2\circ f=\phi _2\circ (\phi _2^{-1}\circ f')=f'$
. This implies that
![]() $\ker (d')=i'$
.
$\ker (d')=i'$
.
We now record a lemma on the intersection of exact subcategories. Note that this is slightly different (and in view of [Reference Rump33, Cor. 2], more general) than [Reference Brüstle, Hassoun, Langford and Roy4, Lem. 5.2].
Lemma 3.2. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Also, let
$({\cal{A}},{\cal{E}})$
be an exact category. Also, let
![]() $({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
be an arbitrary family of exact subcategories of
$({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
be an arbitrary family of exact subcategories of
![]() $({\cal{A}},{\cal{E}})$
. Then
$({\cal{A}},{\cal{E}})$
. Then
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
is exact subcategory of
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
is exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Proof. Clearly,
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
is a strictly full additive subcategory of
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
is a strictly full additive subcategory of
![]() $({\cal{A}},{\cal{E}})$
. By [Reference Bühler6, Def. 2.1] and [Reference Bühler6, Rem. 2.4], it is enough to show that
$({\cal{A}},{\cal{E}})$
. By [Reference Bühler6, Def. 2.1] and [Reference Bühler6, Rem. 2.4], it is enough to show that
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs and
$\cap _{\lambda }{\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs and
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axioms [E0], [E0
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axioms [E0], [E0
![]() $^{\text {op}}$
], [E1
$^{\text {op}}$
], [E1
![]() $^{\text {op}}$
], [E2], and [E2
$^{\text {op}}$
], [E2], and [E2
![]() $^{\text {op}}$
] of [Reference Bühler6, Def. 2.1]. First, we will show that
$^{\text {op}}$
] of [Reference Bühler6, Def. 2.1]. First, we will show that
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs. Let
$\cap _{\lambda }{\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs. Let
be a kernel–cokernel pair in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
, so
$\cap _{\lambda }{\cal{E}}_{\lambda }$
, so
![]() $M,N,L\in {\cal{A}}_{\lambda }$
and
$M,N,L\in {\cal{A}}_{\lambda }$
and
is a kernel–cokernel pair in
![]() ${\cal{A}}_{\lambda }$
for all
${\cal{A}}_{\lambda }$
for all
![]() $\lambda $
. Also, let
$\lambda $
. Also, let
![]() $M'\to N'\to L'$
be a kernel–cokernel pair in
$M'\to N'\to L'$
be a kernel–cokernel pair in
![]() $\cap _{\lambda }{\cal{A}}_{\lambda }$
such that it is isomorphic to
$\cap _{\lambda }{\cal{A}}_{\lambda }$
such that it is isomorphic to
. So,
![]() $M',N',L'\in {\cal{A}}_{\lambda }$
and
$M',N',L'\in {\cal{A}}_{\lambda }$
and
![]() $M'\to N'$
,
$M'\to N'$
,
![]() $N'\to L'$
are two morphisms in
$N'\to L'$
are two morphisms in
![]() ${\cal{A}}_{\lambda }$
for all
${\cal{A}}_{\lambda }$
for all
![]() $\lambda $
. Hence, by Lemma 3.1, we get that
$\lambda $
. Hence, by Lemma 3.1, we get that
![]() $M'\to N'\to L'$
is a kernel–cokernel pair in
$M'\to N'\to L'$
is a kernel–cokernel pair in
![]() ${\cal{A}}_{\lambda }$
for all
${\cal{A}}_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() $({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact category and
$({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact category and
is in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
, we have
$\lambda $
, we have
is in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. So,
$\lambda $
. So,
is in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. Thus,
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. Thus,
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
is closed under isomorphisms. Next, we will show that
$\cap _{\lambda }{\cal{E}}_{\lambda }$
is closed under isomorphisms. Next, we will show that
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0]. Let
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0]. Let
![]() $A\in \cap _{\lambda } {\cal{A}}_{\lambda }$
. Since
$A\in \cap _{\lambda } {\cal{A}}_{\lambda }$
. Since
![]() $({\cal{A}}_{\lambda }, {\cal{E}}_{\lambda })$
is an exact category for all
$({\cal{A}}_{\lambda }, {\cal{E}}_{\lambda })$
is an exact category for all
![]() $\lambda $
, by [Reference Bühler6, Lem. 2.7], we get that
$\lambda $
, by [Reference Bühler6, Lem. 2.7], we get that
is in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. As
$\lambda $
. As
![]() ${\cal{A}}_{\lambda }$
is an additive subcategory of
${\cal{A}}_{\lambda }$
is an additive subcategory of
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, so
$\lambda $
, so
![]() $0_{\cal{A}}=0_{{\cal{A}}_{\lambda }}$
for all
$0_{\cal{A}}=0_{{\cal{A}}_{\lambda }}$
for all
![]() $\lambda $
. Hence, by definition,
$\lambda $
. Hence, by definition,
is in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
, which implies that
$\cap _{\lambda }{\cal{E}}_{\lambda }$
, which implies that
![]() $1_A$
is an admissible monic in
$1_A$
is an admissible monic in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. So,
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. So,
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0]. Next, we will show that
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0]. Next, we will show that
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0
![]() $^{\text {op}}$
]. Let
$^{\text {op}}$
]. Let
![]() $A\in \cap _{\lambda } {\cal{A}}_{\lambda }$
. Since
$A\in \cap _{\lambda } {\cal{A}}_{\lambda }$
. Since
![]() $({\cal{A}}_{\lambda }, {\cal{E}}_{\lambda })$
is an exact category for all
$({\cal{A}}_{\lambda }, {\cal{E}}_{\lambda })$
is an exact category for all
![]() $\lambda $
, by [Reference Bühler6, Lem. 2.7], we get that
$\lambda $
, by [Reference Bühler6, Lem. 2.7], we get that
is in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. As
$\lambda $
. As
![]() ${\cal{A}}_{\lambda }$
is an additive subcategory of
${\cal{A}}_{\lambda }$
is an additive subcategory of
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, so
$\lambda $
, so
![]() $0_{\cal{A}}=0_{{\cal{A}}_{\lambda }}$
for all
$0_{\cal{A}}=0_{{\cal{A}}_{\lambda }}$
for all
![]() $\lambda $
. Hence, by definition
$\lambda $
. Hence, by definition
is in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
, which implies that
$\cap _{\lambda }{\cal{E}}_{\lambda }$
, which implies that
![]() $1_A$
is an admissible epic in
$1_A$
is an admissible epic in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. So,
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. So,
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E0
![]() $^{\text {op}}$
]. Next, we will show that
$^{\text {op}}$
]. Next, we will show that
![]() $(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E1
$(\cap _{\lambda } {\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E1
![]() $^{\text {op}}$
]. Let
$^{\text {op}}$
]. Let
and
be two admissible epics in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. Then we will show that
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. Then we will show that
is an admissible epic in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. Now,
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. Now,
and
are admissible epics in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() $({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact category for all
$({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact category for all
![]() $\lambda $
, we get
$\lambda $
, we get
is an admissible epic in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. Hence, there exist objects
$\lambda $
. Hence, there exist objects
![]() $D_{\lambda }\in {\cal{A}}_{\lambda }$
and kernel–cokernel pairs
$D_{\lambda }\in {\cal{A}}_{\lambda }$
and kernel–cokernel pairs
in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. So,
$\lambda $
. So,
is in
![]() $\cal{E}$
for all
$\cal{E}$
for all
![]() $\lambda $
. Hence,
$\lambda $
. Hence,
![]() $\sigma _{\lambda }$
is a kernel–cokernel pair in
$\sigma _{\lambda }$
is a kernel–cokernel pair in
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, so by the universal property of kernels, we get that the kernel–cokernel pairs
$\lambda $
, so by the universal property of kernels, we get that the kernel–cokernel pairs
![]() $\sigma _{\lambda }$
’s are all isomorphic to each other. Hence, all the
$\sigma _{\lambda }$
’s are all isomorphic to each other. Hence, all the
![]() $D_{\lambda }$
’s are isomorphic to each other. Now, fix a
$D_{\lambda }$
’s are isomorphic to each other. Now, fix a
![]() $\lambda $
, say
$\lambda $
, say
![]() $\lambda _0$
. Then
$\lambda _0$
. Then
![]() $D_{\lambda _0}\cong D_{\lambda }$
for all
$D_{\lambda _0}\cong D_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() ${\cal{A}}_{\lambda }$
is a strict subcategory of
${\cal{A}}_{\lambda }$
is a strict subcategory of
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $D_{\lambda _0}\in \cap _{\lambda }{\cal{A}}_{\lambda }$
. Now,
$D_{\lambda _0}\in \cap _{\lambda }{\cal{A}}_{\lambda }$
. Now,
![]() ${\cal{A}}_{\lambda }$
is a strictly full subcategory of
${\cal{A}}_{\lambda }$
is a strictly full subcategory of
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, so
$\lambda $
, so
![]() $D_{\lambda _0}\in {\cal{A}}_{\lambda }$
implies that
$D_{\lambda _0}\in {\cal{A}}_{\lambda }$
implies that
![]() $\sigma _{\lambda _0}$
is a kernel–cokernel pair in
$\sigma _{\lambda _0}$
is a kernel–cokernel pair in
![]() ${\cal{A}}_{\lambda }$
for all
${\cal{A}}_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() ${\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs in
${\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs in
![]() ${\cal{A}}_{\lambda }$
and
${\cal{A}}_{\lambda }$
and
![]() $\sigma _{\lambda }$
’s are all isomorphic to each other, we get
$\sigma _{\lambda }$
’s are all isomorphic to each other, we get
![]() $\sigma _{\lambda _0}\in {\cal{E}}_{\lambda }$
for all
$\sigma _{\lambda _0}\in {\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. So,
$\lambda $
. So,
![]() $\sigma _{\lambda _0}\in \cap _{\lambda }{\cal{E}}_{\lambda }$
. Hence,
$\sigma _{\lambda _0}\in \cap _{\lambda }{\cal{E}}_{\lambda }$
. Hence,
is in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
, so
$\cap _{\lambda }{\cal{E}}_{\lambda }$
, so
is an admissible epic in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. Thus,
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. Thus,
![]() $(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E1
$(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E1
![]() $^{\text {op}}$
]. Now, we will show that
$^{\text {op}}$
]. Now, we will show that
![]() $(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E2]. Let
$(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E2]. Let
be an admissible monic in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
, and let
$\cap _{\lambda }{\cal{E}}_{\lambda }$
, and let
![]() $A\xrightarrow {f}A'$
be an arbitrary morphism in
$A\xrightarrow {f}A'$
be an arbitrary morphism in
![]() $\cap _{\lambda }{\cal{A}}_{\lambda }$
. Now,
$\cap _{\lambda }{\cal{A}}_{\lambda }$
. Now,
is an admissible monic in
![]() ${\cal{E}}_{\lambda }$
for all
${\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() $({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact category for all
$({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact category for all
![]() $\lambda $
, by [Reference Bühler6, Prop. 2.12(iv)], we have the following pushout commutative diagram with rows being kernel–cokernel pairs in
$\lambda $
, by [Reference Bühler6, Prop. 2.12(iv)], we have the following pushout commutative diagram with rows being kernel–cokernel pairs in
![]() ${\cal{E}}_{\lambda }$
:
${\cal{E}}_{\lambda }$
:

Since
![]() $({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact subcategory of
$({\cal{A}}_{\lambda },{\cal{E}}_{\lambda })$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
, by [Reference Bühler6, Prop. 5.2], we get that the square
$({\cal{A}},{\cal{E}})$
, by [Reference Bühler6, Prop. 5.2], we get that the square

is a pushout square in
![]() $\cal{E}$
for all
$\cal{E}$
for all
![]() $\lambda $
. Then, by the universal property of pushout, we get that the kernel–cokernel pairs
$\lambda $
. Then, by the universal property of pushout, we get that the kernel–cokernel pairs
![]() $\beta _{\lambda }$
’s are all isomorphic to each other, so all the
$\beta _{\lambda }$
’s are all isomorphic to each other, so all the
![]() $B^{\prime }_{\lambda }$
’s are isomorphic to each other. Now, fix a
$B^{\prime }_{\lambda }$
’s are isomorphic to each other. Now, fix a
![]() $\lambda $
, say
$\lambda $
, say
![]() $\lambda _0$
. Then
$\lambda _0$
. Then
![]() $B^{\prime }_{\lambda _0}\cong B^{\prime }_{\lambda }$
for all
$B^{\prime }_{\lambda _0}\cong B^{\prime }_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() ${\cal{A}}_{\lambda }$
is a strict subcategory of
${\cal{A}}_{\lambda }$
is a strict subcategory of
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $B^{\prime }_{\lambda _0}\in \cap _{\lambda }{\cal{A}}_{\lambda }$
. Now,
$B^{\prime }_{\lambda _0}\in \cap _{\lambda }{\cal{A}}_{\lambda }$
. Now,
![]() ${\cal{A}}_{\lambda }$
is a strictly full subcategory of
${\cal{A}}_{\lambda }$
is a strictly full subcategory of
![]() $\cal{A}$
for all
$\cal{A}$
for all
![]() $\lambda $
, so
$\lambda $
, so
![]() $B^{\prime }_{\lambda _0}\in {\cal{A}}_{\lambda }$
implies that
$B^{\prime }_{\lambda _0}\in {\cal{A}}_{\lambda }$
implies that
![]() $\beta _{\lambda _0}$
is a kernel–cokernel pair in
$\beta _{\lambda _0}$
is a kernel–cokernel pair in
![]() ${\cal{A}}_{\lambda }$
for all
${\cal{A}}_{\lambda }$
for all
![]() $\lambda $
. Since
$\lambda $
. Since
![]() ${\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs in
${\cal{E}}_{\lambda }$
is closed under isomorphisms of kernel–cokernel pairs in
![]() ${\cal{A}}_{\lambda }$
and
${\cal{A}}_{\lambda }$
and
![]() $\beta _{\lambda }$
’s are all isomorphic to each other, we have
$\beta _{\lambda }$
’s are all isomorphic to each other, we have
![]() $\beta _{\lambda _0}\in {\cal{E}}_{\lambda }$
for all
$\beta _{\lambda _0}\in {\cal{E}}_{\lambda }$
for all
![]() $\lambda $
. So,
$\lambda $
. So,
![]() $\beta _{\lambda _0}\in \cap _{\lambda }{\cal{E}}_{\lambda }$
. Hence,
$\beta _{\lambda _0}\in \cap _{\lambda }{\cal{E}}_{\lambda }$
. Hence,
is in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
, so
$\cap _{\lambda }{\cal{E}}_{\lambda }$
, so
is an admissible monic in
![]() $\cap _{\lambda }{\cal{E}}_{\lambda }$
. Thus,
$\cap _{\lambda }{\cal{E}}_{\lambda }$
. Thus,
![]() $(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E2]. A dual argument will show that
$(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E2]. A dual argument will show that
![]() $(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E2
$(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
satisfies the axiom [E2
![]() $^{\text {op}}$
]. Hence,
$^{\text {op}}$
]. Hence,
![]() $(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
is an exact subcategory of
$(\cap _{\lambda }{\cal{A}}_{\lambda },\cap _{\lambda }{\cal{E}}_{\lambda })$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Next, we record a useful lemma for proving the exactness of certain structures on additive subcategories of a given exact category.
Lemma 3.3. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() ${\cal{A}}'$
be a strictly full additive subcategory of
${\cal{A}}'$
be a strictly full additive subcategory of
![]() $\cal{A}$
. Define
$\cal{A}$
. Define
![]() . If the pullback (resp. pushout) in
. If the pullback (resp. pushout) in
![]() $\cal{A}$
of every
$\cal{A}$
of every
![]() $\mathcal E$
-deflation (resp. inflation) of sequences in
$\mathcal E$
-deflation (resp. inflation) of sequences in
![]() $\mathcal E|_{\cal{A}'}$
along every morphism in
$\mathcal E|_{\cal{A}'}$
along every morphism in
![]() $\mathcal A'$
is again in
$\mathcal A'$
is again in
![]() $\mathcal A'$
, then
$\mathcal A'$
, then
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
The proof of Lemma 3.3 depends on Lemma 3.1 and the following proposition.
Proposition 3.4. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Suppose that we have the following diagram:
$({\cal{A}},{\cal{E}})$
be an exact category. Suppose that we have the following diagram:

where the square commutative diagram is a pullback diagram and
![]() $e,p$
are admissible epics and i is a kernel of p. Then
$e,p$
are admissible epics and i is a kernel of p. Then
![]() $i'$
is an admissible monic with a cokernel given by
$i'$
is an admissible monic with a cokernel given by
.
Proof. The proof follows from the construction in the proof of [Reference Bühler6, Prop. 2.15]. The only missing point in the proof of [Reference Bühler6, Prop. 2.15], toward showing
![]() $i'$
is a kernel of
$i'$
is a kernel of
![]() $p\circ e$
, is the following: it was not shown that
$p\circ e$
, is the following: it was not shown that
![]() $(p\circ e)\circ i'=0$
. This can be easily checked as follows:
$(p\circ e)\circ i'=0$
. This can be easily checked as follows:
![]() $(p\circ e)\circ i'=p\circ (e\circ i')=p\circ (i\circ e')=(p\circ i)\circ e'=0\circ e'=0$
, since i is a kernel of p.
$(p\circ e)\circ i'=p\circ (e\circ i')=p\circ (i\circ e')=(p\circ i)\circ e'=0\circ e'=0$
, since i is a kernel of p.
Proof of Lemma 3.3
Clearly, each kernel–cokernel pair in
![]() ${\cal{E}}|_{\cal{A}'}$
is a kernel–cokernel pair in
${\cal{E}}|_{\cal{A}'}$
is a kernel–cokernel pair in
![]() $\cal{A}$
, hence also a kernel–cokernel pair in
$\cal{A}$
, hence also a kernel–cokernel pair in
![]() $\cal{A}'$
. Thus,
$\cal{A}'$
. Thus,
![]() ${\cal{E}}|_{\cal{A}'}$
consists of kernel–cokernel pairs in
${\cal{E}}|_{\cal{A}'}$
consists of kernel–cokernel pairs in
![]() $\cal{A}'$
. Now, we will show that
$\cal{A}'$
. Now, we will show that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E2]. Let
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E2]. Let
![]() $A,B,A'\in {\cal{A}}'$
, let
$A,B,A'\in {\cal{A}}'$
, let
be an admissible monic in
![]() ${\cal{E}}|_{\cal{A}'}$
, and let
${\cal{E}}|_{\cal{A}'}$
, and let
![]() $A\xrightarrow {f}A'$
be an arbitrary morphism in
$A\xrightarrow {f}A'$
be an arbitrary morphism in
![]() ${\cal{A}}'$
. Now,
${\cal{A}}'$
. Now,
is an admissible monic in
![]() $\cal{E}$
. Since
$\cal{E}$
. Since
![]() $({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Prop. 2.12(iv)], we have the following pushout commutative diagram with rows being kernel–cokernel pairs in
$({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Prop. 2.12(iv)], we have the following pushout commutative diagram with rows being kernel–cokernel pairs in
![]() $\cal{E}$
:
$\cal{E}$
:

Now, by the assumption, we have
![]() $B'\in {\cal{A}}'$
. Since
$B'\in {\cal{A}}'$
. Since
is an admissible monic in
![]() ${\cal{E}}|_{\cal{A}'}$
, we have
${\cal{E}}|_{\cal{A}'}$
, we have
![]() $C\in {\cal{A}}'$
. Thus,
$C\in {\cal{A}}'$
. Thus,
![]() $\beta \in {\cal{E}}|_{\cal{A}'}$
. Since
$\beta \in {\cal{E}}|_{\cal{A}'}$
. Since
![]() $\cal{A}'$
is a strictly full subcategory of
$\cal{A}'$
is a strictly full subcategory of
![]() $\cal{A}$
, the above diagram is a pushout diagram in
$\cal{A}$
, the above diagram is a pushout diagram in
![]() $\cal{A}'$
as well. Thus,
$\cal{A}'$
as well. Thus,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E2]. Similarly,
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E2]. Similarly,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E2
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E2
![]() $^{\text {op}}$
]. Now, by [Reference Bühler6, Def. 2.1] and [Reference Bühler6, Rem. 2.4], it is enough to show that
$^{\text {op}}$
]. Now, by [Reference Bühler6, Def. 2.1] and [Reference Bühler6, Rem. 2.4], it is enough to show that
![]() ${\cal{E}}|_{\cal{A}'}$
is closed under isomorphisms and
${\cal{E}}|_{\cal{A}'}$
is closed under isomorphisms and
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axioms [E0], [E0
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axioms [E0], [E0
![]() $^{\text {op}}$
], and [E1
$^{\text {op}}$
], and [E1
![]() $^{\text {op}}$
]. First, we will show that
$^{\text {op}}$
]. First, we will show that
![]() ${\cal{E}}|_{\cal{A}'}$
is closed under isomorphisms. Let
${\cal{E}}|_{\cal{A}'}$
is closed under isomorphisms. Let
be a kernel–cokernel pair in
![]() ${\cal{E}}|_{\cal{A}'}$
, so
${\cal{E}}|_{\cal{A}'}$
, so
![]() $M,N,L\in {\cal{A}}'$
and
$M,N,L\in {\cal{A}}'$
and
is a kernel–cokernel pair in
![]() $\cal{A}$
. Also, let
$\cal{A}$
. Also, let
![]() $M'\to N'\to L'$
be a kernel–cokernel pair in
$M'\to N'\to L'$
be a kernel–cokernel pair in
![]() $\cal{A}'$
such that it is isomorphic to
$\cal{A}'$
such that it is isomorphic to
. Hence, by Lemma 3.1, we get that
![]() $M'\to N'\to L'$
is a kernel–cokernel pair in
$M'\to N'\to L'$
is a kernel–cokernel pair in
![]() $\cal{A}$
. Since
$\cal{A}$
. Since
![]() $({\cal{A}},{\cal{E}})$
is an exact category, we have
$({\cal{A}},{\cal{E}})$
is an exact category, we have
is in
![]() ${\cal{E}}$
. Hence, by definition,
${\cal{E}}$
. Hence, by definition,
is in
![]() ${\cal{E}}|_{\cal{A}'}$
. Thus,
${\cal{E}}|_{\cal{A}'}$
. Thus,
![]() ${\cal{E}}|_{\cal{A}'}$
is closed under isomorphisms. Next, we will show that
${\cal{E}}|_{\cal{A}'}$
is closed under isomorphisms. Next, we will show that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0]. Let
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0]. Let
![]() $A\in {\cal{A}}'$
. Since
$A\in {\cal{A}}'$
. Since
![]() $({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
$({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
is in
![]() ${\cal{E}}$
. As
${\cal{E}}$
. As
![]() $\cal{A}'$
is an additive subcategory of
$\cal{A}'$
is an additive subcategory of
![]() $\cal{A}$
, so
$\cal{A}$
, so
![]() $0_{\cal{A}}=0_{\cal{A}'}$
. Hence, by definition,
$0_{\cal{A}}=0_{\cal{A}'}$
. Hence, by definition,
is in
![]() ${\cal{E}}|_{\cal{A}'}$
, which implies that
${\cal{E}}|_{\cal{A}'}$
, which implies that
![]() $1_A$
is an admissible monic in
$1_A$
is an admissible monic in
![]() ${\cal{E}}|_{\cal{A}'}$
. So,
${\cal{E}}|_{\cal{A}'}$
. So,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0]. Next, we will show that
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0]. Next, we will show that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0
![]() $^{\text {op}}$
]. Let
$^{\text {op}}$
]. Let
![]() $A\in {\cal{A}}'$
. Since
$A\in {\cal{A}}'$
. Since
![]() $({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
$({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
is in
![]() ${\cal{E}}$
. As
${\cal{E}}$
. As
![]() $\cal{A}'$
is an additive subcategory of
$\cal{A}'$
is an additive subcategory of
![]() $\cal{A}$
, so
$\cal{A}$
, so
![]() $0_{\cal{A}}=0_{\cal{A}'}$
. Hence, by definition,
$0_{\cal{A}}=0_{\cal{A}'}$
. Hence, by definition,
is in
![]() ${\cal{E}}|_{\cal{A}'}$
, which implies that
${\cal{E}}|_{\cal{A}'}$
, which implies that
![]() $1_A$
is an admissible epic in
$1_A$
is an admissible epic in
![]() ${\cal{E}}|_{\cal{A}'}$
. So,
${\cal{E}}|_{\cal{A}'}$
. So,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E0
![]() $^{\text {op}}$
]. Next, we will show that
$^{\text {op}}$
]. Next, we will show that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E1
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E1
![]() $^{\text {op}}$
]. Let
$^{\text {op}}$
]. Let
and
be two admissible epics in
![]() $\cal{E}$
such that they are in
$\cal{E}$
such that they are in
![]() ${\cal{E}}|_{\cal{A}'}$
, which means that there exist two kernel–cokernel pairs
${\cal{E}}|_{\cal{A}'}$
, which means that there exist two kernel–cokernel pairs
and
in
![]() $\cal{E}$
such that
$\cal{E}$
such that
![]() $A,B,C,D,B'\in {\cal{A}}'$
. Then we will show that
$A,B,C,D,B'\in {\cal{A}}'$
. Then we will show that
is an admissible epic in
![]() ${\cal{E}}|_{\cal{A}'}$
. From Proposition 3.4, we get that
${\cal{E}}|_{\cal{A}'}$
. From Proposition 3.4, we get that
is a kernel–cokernel pair in
![]() $\cal{E}$
. By the hypothesis of Lemma 3.3 and the diagram of Proposition 3.4, we get that
$\cal{E}$
. By the hypothesis of Lemma 3.3 and the diagram of Proposition 3.4, we get that
![]() $A'\in {\cal{A}}'$
. Hence,
$A'\in {\cal{A}}'$
. Hence,
is an admissible epic in
![]() ${\cal{E}}|_{\cal{A}'}$
. Thus,
${\cal{E}}|_{\cal{A}'}$
. Thus,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E1
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
satisfies the axiom [E1
![]() $^{\text {op}}$
]. So,
$^{\text {op}}$
]. So,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
From now on, given a subcategory
![]() $\cal{A}'$
of an exact category
$\cal{A}'$
of an exact category
![]() $({\cal{A}},{\cal{E}})$
, the notation
$({\cal{A}},{\cal{E}})$
, the notation
![]() ${\cal{E}}|_{\cal{A}'}$
will stand for as defined in Lemma 3.3. Using Lemma 3.3, we now record two quick consequences, which give a sufficient condition on a subcategory
${\cal{E}}|_{\cal{A}'}$
will stand for as defined in Lemma 3.3. Using Lemma 3.3, we now record two quick consequences, which give a sufficient condition on a subcategory
![]() $\cal{A}'$
such that
$\cal{A}'$
such that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
. The first of which we state below now is well known (see, e.g., [Reference Bühler6, Lem. 10.20]). However, due to the absence of a proof in [Reference Bühler6, Lem. 10.20], we give a proof using our Lemma 3.3.
$({\cal{A}},{\cal{E}})$
. The first of which we state below now is well known (see, e.g., [Reference Bühler6, Lem. 10.20]). However, due to the absence of a proof in [Reference Bühler6, Lem. 10.20], we give a proof using our Lemma 3.3.
Proposition 3.5. (cf. [Reference Bühler6, Lem. 10.20]) Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\cal{A}'$
be a strictly full additive subcategory of
$\cal{A}'$
be a strictly full additive subcategory of
![]() $\cal{A}$
. Assume that for every
$\cal{A}$
. Assume that for every
![]() $X\to Y\to Z$
in
$X\to Y\to Z$
in
![]() ${\cal{E}}$
, if
${\cal{E}}$
, if
![]() $X,Z\in {\cal{A}}'$
, then
$X,Z\in {\cal{A}}'$
, then
![]() $Y\in {\cal{A}}'$
(i.e.,
$Y\in {\cal{A}}'$
(i.e.,
![]() $\cal{A}'$
is closed under extensions). Then
$\cal{A}'$
is closed under extensions). Then
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Proof. By Lemma 3.3, it is enough to show that the pullback (resp. pushout) in
![]() $\cal{A}$
of every
$\cal{A}$
of every
![]() $\mathcal E$
-deflation (resp. inflation) of sequences in
$\mathcal E$
-deflation (resp. inflation) of sequences in
![]() $\mathcal E|_{\cal{A}'}$
along every morphism in
$\mathcal E|_{\cal{A}'}$
along every morphism in
![]() $\mathcal A'$
is again in
$\mathcal A'$
is again in
![]() $\mathcal A'$
. Let
$\mathcal A'$
. Let
be an inflation in
![]() $\mathcal E|_{\cal{A}'}$
, and let
$\mathcal E|_{\cal{A}'}$
, and let
![]() $f:A\to A'$
be a morphism in
$f:A\to A'$
be a morphism in
![]() $\mathcal A'$
. Then, by [Reference Bühler6, Prop. 2.12(iv)], we get the following pushout commutative diagram:
$\mathcal A'$
. Then, by [Reference Bühler6, Prop. 2.12(iv)], we get the following pushout commutative diagram:

Since
![]() $A',C\in {\cal{A}}'$
, by assumption and the bottom row of the above diagram, we get that
$A',C\in {\cal{A}}'$
, by assumption and the bottom row of the above diagram, we get that
![]() $B'\in {\cal{A}}'$
. The pullback case follows by a dual argument. Hence,
$B'\in {\cal{A}}'$
. The pullback case follows by a dual argument. Hence,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Theorem 3.6. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\cal{A}'$
be a strictly full additive subcategory of
$\cal{A}'$
be a strictly full additive subcategory of
![]() $\cal{A}$
. Assume that
$\cal{A}$
. Assume that
![]() $\cal{A}'$
is closed under kernels and co-kernels of admissible epics and monics in
$\cal{A}'$
is closed under kernels and co-kernels of admissible epics and monics in
![]() $\cal{E}$
, respectively. Then,
$\cal{E}$
, respectively. Then,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Proof. By Lemma 3.3, it is enough to show that the pullback (resp. pushout) in
![]() $\cal{A}$
of every
$\cal{A}$
of every
![]() $\mathcal E$
-deflation (resp. inflation) of sequences in
$\mathcal E$
-deflation (resp. inflation) of sequences in
![]() $\mathcal E|_{\cal{A}'}$
along every morphism in
$\mathcal E|_{\cal{A}'}$
along every morphism in
![]() $\mathcal A'$
is again in
$\mathcal A'$
is again in
![]() $\mathcal A'$
. Let
$\mathcal A'$
. Let
be an inflation in
![]() $\mathcal E|_{\cal{A}'}$
, and let
$\mathcal E|_{\cal{A}'}$
, and let
![]() $f:A\to A'$
be a morphism in
$f:A\to A'$
be a morphism in
![]() $\mathcal A'$
. Now, we have the following pushout commutative diagram in
$\mathcal A'$
. Now, we have the following pushout commutative diagram in
![]() $(A,{\cal{E}})$
:
$(A,{\cal{E}})$
:

Then, by [Reference Bühler6, Prop. 2.12(ii)], we have the following kernel–cokernel pair in
![]() ${\cal{E}}$
:
${\cal{E}}$
:
. As
![]() $B,A'\in {\cal{A}}'$
and
$B,A'\in {\cal{A}}'$
and
![]() $\cal{A}'$
is additive, so
$\cal{A}'$
is additive, so
![]() $B\oplus A'\in {\cal{A}}'$
. Since
$B\oplus A'\in {\cal{A}}'$
. Since
is an admissible monic in
![]() $\cal{E}$
, we get the cokernel
$\cal{E}$
, we get the cokernel
![]() $B'\in {\cal{A}}'$
. The pullback case follows by a dual argument. Hence,
$B'\in {\cal{A}}'$
. The pullback case follows by a dual argument. Hence,
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Given any exact category
![]() $({\cal{A}},{\cal{E}})$
and
$({\cal{A}},{\cal{E}})$
and
![]() $C,A\in {\cal{A}}$
, one can define the Yoneda Ext group
$C,A\in {\cal{A}}$
, one can define the Yoneda Ext group
![]() ${\operatorname{Ext}}_{\cal{E}}(C,A)$
, which has an abelian group structure by Baer sum (see the beginning of [Reference Dräxler, Reiten, Smalø and Solberg14, §1.2] for a description of
${\operatorname{Ext}}_{\cal{E}}(C,A)$
, which has an abelian group structure by Baer sum (see the beginning of [Reference Dräxler, Reiten, Smalø and Solberg14, §1.2] for a description of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)$
). When
${\operatorname{Ext}}_{\cal{E}}(-,-)$
). When
![]() $({\cal{A}},{\cal{E}})$
is moreover an R-linear category, then
$({\cal{A}},{\cal{E}})$
is moreover an R-linear category, then
![]() ${\operatorname{Ext}}_{\cal{E}}(C,A)$
can be given an R-linear structure via either of the following constructions, both of which yield equivalent triples in
${\operatorname{Ext}}_{\cal{E}}(C,A)$
can be given an R-linear structure via either of the following constructions, both of which yield equivalent triples in
![]() ${\operatorname{Ext}}_{\cal{E}}(C,A)$
:
${\operatorname{Ext}}_{\cal{E}}(C,A)$
:
Given a kernel–cokernel pair
in
![]() ${\operatorname{Ext}}_{\cal{E}}(C,A)$
, the multiplication
${\operatorname{Ext}}_{\cal{E}}(C,A)$
, the multiplication
![]() $r\cdot \sigma $
is either given by the following pullback diagram:
$r\cdot \sigma $
is either given by the following pullback diagram:

or by the following pushout diagram:

That both of these yield equivalent triplet in
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)$
follows from [Reference Bühler6, Prop. 3.1]. Moreover, this makes
${\operatorname{Ext}}_{\cal{E}}(-,-)$
follows from [Reference Bühler6, Prop. 3.1]. Moreover, this makes
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)$
into an R-linear functor in each component.
${\operatorname{Ext}}_{\cal{E}}(-,-)$
into an R-linear functor in each component.
Now, we show that if
![]() $({\cal{A}}',{\cal{E}'})$
is a strictly full exact subcategory of an exact category
$({\cal{A}}',{\cal{E}'})$
is a strictly full exact subcategory of an exact category
![]() $({\cal{A}},{\cal{E}})$
, then
$({\cal{A}},{\cal{E}})$
, then
![]() ${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
is naturally a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
is naturally a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
. For this, we first record a remark.
${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
. For this, we first record a remark.
Remark 3.7. Let
![]() $({\cal{A}}',{\cal{E}} ')$
be a strictly full exact subcategory of
$({\cal{A}}',{\cal{E}} ')$
be a strictly full exact subcategory of
![]() $(\cal{A},{\cal{E}})$
. Then, for
$(\cal{A},{\cal{E}})$
. Then, for
![]() $\sigma \in {\cal{E}} ' (\subseteq {\cal{E}})$
, it is actually true that
$\sigma \in {\cal{E}} ' (\subseteq {\cal{E}})$
, it is actually true that
![]() $[\sigma ]_{\cal{E} '}=[\sigma ]_{\cal{E}}$
; hence, the map
$[\sigma ]_{\cal{E} '}=[\sigma ]_{\cal{E}}$
; hence, the map
![]() ${\operatorname{Ext}}_{\cal{E} '}(-,-)\xrightarrow {[\sigma ]_{\cal{E} '}\mapsto [\sigma ]_{\cal{E}}} {\operatorname{Ext}}_{\cal{E}}(-,-)$
is the natural inclusion map. Indeed, to see
${\operatorname{Ext}}_{\cal{E} '}(-,-)\xrightarrow {[\sigma ]_{\cal{E} '}\mapsto [\sigma ]_{\cal{E}}} {\operatorname{Ext}}_{\cal{E}}(-,-)$
is the natural inclusion map. Indeed, to see
![]() $[\sigma ]_{\cal{E} '}=[\sigma ]_{\cal{E}}$
: let
$[\sigma ]_{\cal{E} '}=[\sigma ]_{\cal{E}}$
: let
![]() $\sigma $
be a kernel–cokernel pair
$\sigma $
be a kernel–cokernel pair
in
![]() ${\cal{E}}'$
, so
${\cal{E}}'$
, so
![]() $A,B,C\in {\cal{A}}'$
. Let
$A,B,C\in {\cal{A}}'$
. Let
![]() $\beta \in [\sigma ]_{\cal{E}}$
be the kernel–cokernel pair
$\beta \in [\sigma ]_{\cal{E}}$
be the kernel–cokernel pair
in
![]() $\cal{E}$
, so
$\cal{E}$
, so
![]() $B'\in {\cal{A}}$
. Hence, there exists
$B'\in {\cal{A}}$
. Hence, there exists
![]() $f\in \operatorname{Mor}_{\cal{A}}(B,B')$
such that we have the following commutative diagram in
$f\in \operatorname{Mor}_{\cal{A}}(B,B')$
such that we have the following commutative diagram in
![]() $\cal{A}$
:
$\cal{A}$
:

By [Reference Bühler6, Cor. 3.2], we get that f is an isomorphism. Since
![]() $B\in {\cal{A}}'$
,
$B\in {\cal{A}}'$
,
![]() $B'\in {\cal{A}}$
, and
$B'\in {\cal{A}}$
, and
![]() $\cal{A}'$
is a strict subcategory of
$\cal{A}'$
is a strict subcategory of
![]() $\cal{A}$
,
$\cal{A}$
,
![]() $B\cong B'$
implies that
$B\cong B'$
implies that
![]() $B'\in {\cal{A}}'$
. Since
$B'\in {\cal{A}}'$
. Since
![]() $\cal{A}'$
is full,
$\cal{A}'$
is full,
![]() $f\in \operatorname{Mor}_{\cal{A}'}(B,B')$
. Hence, the above commutative diagram is in
$f\in \operatorname{Mor}_{\cal{A}'}(B,B')$
. Hence, the above commutative diagram is in
![]() $\cal{A}'$
. Since
$\cal{A}'$
. Since
![]() $({\cal{A}}',{\cal{E}}')$
is an exact category,
$({\cal{A}}',{\cal{E}}')$
is an exact category,
![]() ${\cal{E}}'$
is closed under isomorphisms. Hence,
${\cal{E}}'$
is closed under isomorphisms. Hence,
![]() $\beta \in {\cal{E}}'$
and
$\beta \in {\cal{E}}'$
and
![]() $\beta \in [\sigma ]_{\cal{E}'}$
. Thus,
$\beta \in [\sigma ]_{\cal{E}'}$
. Thus,
![]() $[\sigma ]_{\cal{E}}\subseteq [\sigma ]_{\cal{E}'}$
. Now,
$[\sigma ]_{\cal{E}}\subseteq [\sigma ]_{\cal{E}'}$
. Now,
![]() $({\cal{A}}',{\cal{E}}')$
is a subcategory of
$({\cal{A}}',{\cal{E}}')$
is a subcategory of
![]() $({\cal{A}},{\cal{E}})$
, so
$({\cal{A}},{\cal{E}})$
, so
![]() $[\sigma ]_{\cal{E}'}\subseteq [\sigma ]_{\cal{E}}$
as well. Hence,
$[\sigma ]_{\cal{E}'}\subseteq [\sigma ]_{\cal{E}}$
as well. Hence,
![]() $[\sigma ]_{\cal{E}'}=[\sigma ]_{\cal{E}}$
.
$[\sigma ]_{\cal{E}'}=[\sigma ]_{\cal{E}}$
.
Proposition 3.8. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $({\cal{A}}',{\cal{E}}')$
be a strictly full exact subcategory of
$({\cal{A}}',{\cal{E}}')$
be a strictly full exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
. Then
$({\cal{A}},{\cal{E}})$
. Then
![]() ${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
, where for every
${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
, where for every
![]() $C,A\in {\cal{A}}'$
, the natural inclusion map
$C,A\in {\cal{A}}'$
, the natural inclusion map
![]() ${\operatorname{Ext}}_{\cal{E}'}(C,A)\to {\operatorname{Ext}}_{\cal{E}}(C,A)$
is given by
${\operatorname{Ext}}_{\cal{E}'}(C,A)\to {\operatorname{Ext}}_{\cal{E}}(C,A)$
is given by
![]() $[\sigma ]_{\cal{E}'} \mapsto [\sigma ]_{\cal{E}}$
. If
$[\sigma ]_{\cal{E}'} \mapsto [\sigma ]_{\cal{E}}$
. If
![]() ${\cal{A}}$
is moreover R-linear, then the natural inclusion map is also R-linear; hence,
${\cal{A}}$
is moreover R-linear, then the natural inclusion map is also R-linear; hence,
![]() ${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}'}^{\operatorname{op}}\times {\cal{A}'}\to {\operatorname{mod}}\ R$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}'}^{\operatorname{op}}\times {\cal{A}'}\to {\operatorname{mod}}\ R$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}'}^{\operatorname{op}}\times {\cal{A}}'}:{\cal{A}'}^{\operatorname{op}}\times {\cal{A}}'\to {\operatorname{mod}}\ R$
.
${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}'}^{\operatorname{op}}\times {\cal{A}}'}:{\cal{A}'}^{\operatorname{op}}\times {\cal{A}}'\to {\operatorname{mod}}\ R$
.
Proof. Let
![]() $C,A\in {\cal{A}}'$
. Define
$C,A\in {\cal{A}}'$
. Define
![]() $\phi _{C,A}:{\operatorname{Ext}}_{\cal{E}'}(C,A)\to {\operatorname{Ext}}_{\cal{E}}(C,A)$
by
$\phi _{C,A}:{\operatorname{Ext}}_{\cal{E}'}(C,A)\to {\operatorname{Ext}}_{\cal{E}}(C,A)$
by
![]() $\phi _{C,A}([\sigma ]_{\cal{E}'})=[\sigma ]_{\cal{E}}$
. From now on, we will call this map
$\phi _{C,A}([\sigma ]_{\cal{E}'})=[\sigma ]_{\cal{E}}$
. From now on, we will call this map
![]() $\phi $
. The well-definedness and injectivity of
$\phi $
. The well-definedness and injectivity of
![]() $\phi $
follow from Remark 3.7. Next, we will show that
$\phi $
follow from Remark 3.7. Next, we will show that
![]() $\phi $
is a group homomorphism. Let
$\phi $
is a group homomorphism. Let
![]() $[\sigma ]_{\cal{E}'},[\beta ]_{\cal{E}'}\in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
, where
$[\sigma ]_{\cal{E}'},[\beta ]_{\cal{E}'}\in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
, where
and
for some
![]() $B,B'\in {\cal{A}}'$
. Then
$B,B'\in {\cal{A}}'$
. Then
![]() $[\sigma ]_{\cal{E}'}+[\beta ]_{\cal{E}'}=[\alpha ]_{\cal{E}'}$
is given by the following commutative diagram in
$[\sigma ]_{\cal{E}'}+[\beta ]_{\cal{E}'}=[\alpha ]_{\cal{E}'}$
is given by the following commutative diagram in
![]() $({\cal{A}}',{\cal{E}}')$
:
$({\cal{A}}',{\cal{E}}')$
:

We know that
![]() $\gamma $
is the pushout of
$\gamma $
is the pushout of
![]() $\sigma \oplus \beta $
in
$\sigma \oplus \beta $
in
![]() $\cal{E}'$
by the sum map
$\cal{E}'$
by the sum map
![]() $A\oplus A\xrightarrow {\Sigma }A$
. Since
$A\oplus A\xrightarrow {\Sigma }A$
. Since
![]() $({\cal{A}}',{\cal{E}}')$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}')$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
, by [Reference Bühler6, Prop. 5.2], we get that
$({\cal{A}},{\cal{E}})$
, by [Reference Bühler6, Prop. 5.2], we get that
![]() $\gamma $
is also the pushout of
$\gamma $
is also the pushout of
![]() $\sigma \oplus \beta $
in
$\sigma \oplus \beta $
in
![]() ${\cal{E}}$
by the sum map
${\cal{E}}$
by the sum map
![]() $A\oplus A\xrightarrow {\Sigma }A$
. Next,
$A\oplus A\xrightarrow {\Sigma }A$
. Next,
![]() $\alpha $
is the pullback of
$\alpha $
is the pullback of
![]() $\gamma $
in
$\gamma $
in
![]() $\cal{E}'$
by the diagonal map
$\cal{E}'$
by the diagonal map
![]() $C\xrightarrow {\Delta } C\oplus C$
, so by [Reference Bühler6, Prop. 5.2] we get that
$C\xrightarrow {\Delta } C\oplus C$
, so by [Reference Bühler6, Prop. 5.2] we get that
![]() $\alpha $
is also the pullback of
$\alpha $
is also the pullback of
![]() $\gamma $
in
$\gamma $
in
![]() $\cal{E}$
by the diagonal map
$\cal{E}$
by the diagonal map
![]() $C\xrightarrow {\Delta } C\oplus C$
. This implies that
$C\xrightarrow {\Delta } C\oplus C$
. This implies that
![]() $\alpha $
is a representative of
$\alpha $
is a representative of
![]() $[\sigma ]_{\cal{E}}+[\beta ]_{\cal{E}}$
in
$[\sigma ]_{\cal{E}}+[\beta ]_{\cal{E}}$
in
![]() ${\operatorname{Ext}}_{\cal{E}}(C,A)$
, that is,
${\operatorname{Ext}}_{\cal{E}}(C,A)$
, that is,
![]() $[\alpha ]_{\cal{E}}=[\sigma ]_{\cal{E}}+[\beta ]_{\cal{E}}$
. Since
$[\alpha ]_{\cal{E}}=[\sigma ]_{\cal{E}}+[\beta ]_{\cal{E}}$
. Since
![]() $\phi ([\sigma ]_{\cal{E}'}+[\beta ]_{\cal{E}'})=\phi ([\alpha ]_{\cal{E}'})=[\alpha ]_{\cal{E}}$
and
$\phi ([\sigma ]_{\cal{E}'}+[\beta ]_{\cal{E}'})=\phi ([\alpha ]_{\cal{E}'})=[\alpha ]_{\cal{E}}$
and
![]() $\phi ([\sigma ]_{\cal{E}'})+\phi ([\beta ]_{\cal{E}'})=[\sigma ]_{\cal{E}}+[\beta ]_{\cal{E}}$
, we get
$\phi ([\sigma ]_{\cal{E}'})+\phi ([\beta ]_{\cal{E}'})=[\sigma ]_{\cal{E}}+[\beta ]_{\cal{E}}$
, we get
![]() $\phi $
is a group homomorphism.
$\phi $
is a group homomorphism.
Let
![]() $A,B,C\in {\cal{A}}'$
, and let
$A,B,C\in {\cal{A}}'$
, and let
![]() $f\in \operatorname{Mor}_{\cal{A}'}(A,B)$
. First, we will show that
$f\in \operatorname{Mor}_{\cal{A}'}(A,B)$
. First, we will show that
![]() ${\operatorname{Ext}}_{\cal{E}'}(C,-)$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(C,-)$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(C,-)$
, so we need to prove that the following diagram commutes:
${\operatorname{Ext}}_{\cal{E}}(C,-)$
, so we need to prove that the following diagram commutes:

where for every
![]() $[\sigma ]_{\cal{E}} \in {\operatorname{Ext}}_{\cal{E}}(C,A)$
, a representative of
$[\sigma ]_{\cal{E}} \in {\operatorname{Ext}}_{\cal{E}}(C,A)$
, a representative of
![]() $f^*([\sigma ]_{\cal{E}})$
is the pushout of
$f^*([\sigma ]_{\cal{E}})$
is the pushout of
![]() $\sigma $
by f in
$\sigma $
by f in
![]() $\cal{E}$
and for every
$\cal{E}$
and for every
![]() $[\beta ]_{\cal{E}'} \in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
, a representative of
$[\beta ]_{\cal{E}'} \in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
, a representative of
![]() $\tilde {f}([\beta ]_{\cal{E}'})$
is the pushout of
$\tilde {f}([\beta ]_{\cal{E}'})$
is the pushout of
![]() $\beta $
by f in
$\beta $
by f in
![]() $\cal{E}'$
. Let
$\cal{E}'$
. Let
![]() $[\sigma ]_{\cal{E}'}\in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
. Now,
$[\sigma ]_{\cal{E}'}\in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
. Now,
![]() $\phi _{C,A}([\sigma ]_{\cal{E}'})=[\sigma ]_{\cal{E}}$
and
$\phi _{C,A}([\sigma ]_{\cal{E}'})=[\sigma ]_{\cal{E}}$
and
![]() $f^*([\sigma ]_{\cal{E}})=[\gamma ]_{\cal{E}}$
, where
$f^*([\sigma ]_{\cal{E}})=[\gamma ]_{\cal{E}}$
, where
![]() $\gamma $
is the pushout of
$\gamma $
is the pushout of
![]() $\sigma $
by f in
$\sigma $
by f in
![]() $\cal{E}$
. Next, we have
$\cal{E}$
. Next, we have
![]() $\tilde {f}([\sigma ]_{\cal{E}'})=[\alpha ]_{\cal{E}'}$
, where
$\tilde {f}([\sigma ]_{\cal{E}'})=[\alpha ]_{\cal{E}'}$
, where
![]() $\alpha $
is the pushout of
$\alpha $
is the pushout of
![]() $\sigma $
by f in
$\sigma $
by f in
![]() $\cal{E}'$
. Hence, by [Reference Bühler6, Prop. 5.2], we get that
$\cal{E}'$
. Hence, by [Reference Bühler6, Prop. 5.2], we get that
![]() $\alpha $
is also the pushout of
$\alpha $
is also the pushout of
![]() $\sigma $
by f in
$\sigma $
by f in
![]() $\cal{E}$
. Hence,
$\cal{E}$
. Hence,
![]() $[\alpha ]_{\cal{E}}=[\gamma ]_{\cal{E}}$
, so
$[\alpha ]_{\cal{E}}=[\gamma ]_{\cal{E}}$
, so
![]() $\phi _{C,B}(\tilde {f}([\sigma ]_{\cal{E}'}))=\phi _{C,B}([\alpha ]_{\cal{E}'})=[\alpha ]_{\cal{E}}=[\gamma ]_{\cal{E}}=f^*([\sigma ]_{\cal{E}})=f^*(\phi _{C,A}([\sigma ]_{\cal{E}'}))$
, and therefore the above diagram commutes. Hence,
$\phi _{C,B}(\tilde {f}([\sigma ]_{\cal{E}'}))=\phi _{C,B}([\alpha ]_{\cal{E}'})=[\alpha ]_{\cal{E}}=[\gamma ]_{\cal{E}}=f^*([\sigma ]_{\cal{E}})=f^*(\phi _{C,A}([\sigma ]_{\cal{E}'}))$
, and therefore the above diagram commutes. Hence,
![]() ${\operatorname{Ext}}_{\cal{E}'}(C,-)$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(C,-)$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(C,-)$
for any
${\operatorname{Ext}}_{\cal{E}}(C,-)$
for any
![]() $C\in {\cal{A}}'$
. Similarly,
$C\in {\cal{A}}'$
. Similarly,
![]() ${\operatorname{Ext}}_{\cal{E}'}(-,C)$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(-,C)$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,C)$
for any
${\operatorname{Ext}}_{\cal{E}}(-,C)$
for any
![]() $C\in {\cal{A}}'$
. Thus,
$C\in {\cal{A}}'$
. Thus,
![]() ${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(-,-):{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
. Now, let
${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
. Now, let
![]() $\cal{A}$
be R-linear; hence, so is
$\cal{A}$
be R-linear; hence, so is
![]() $\cal{A}'$
because it is a full subcategory of
$\cal{A}'$
because it is a full subcategory of
![]() $\cal{A}$
. Let
$\cal{A}$
. Let
![]() $C,A\in {\cal{A}}'$
, and let
$C,A\in {\cal{A}}'$
, and let
![]() $[\sigma ]_{\cal{E}'}\in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
. Let
$[\sigma ]_{\cal{E}'}\in {\operatorname{Ext}}_{\cal{E}'}(C,A)$
. Let
![]() $[\gamma ]_{\cal{E}'}=r\cdot [\sigma ]_{\cal{E}'}$
, so
$[\gamma ]_{\cal{E}'}=r\cdot [\sigma ]_{\cal{E}'}$
, so
![]() $\gamma $
is obtained from
$\gamma $
is obtained from
![]() $\sigma $
by pullback in
$\sigma $
by pullback in
![]() $\cal{E}'$
along the map
$\cal{E}'$
along the map
![]() $C\xrightarrow {r\cdot \text {id}_C} C$
. Now,
$C\xrightarrow {r\cdot \text {id}_C} C$
. Now,
![]() $({\cal{A}}',{\cal{E}}')$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}')$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
; hence, this is also the pullback in
$({\cal{A}},{\cal{E}})$
; hence, this is also the pullback in
![]() $\cal{E}$
along the map
$\cal{E}$
along the map
![]() $C\xrightarrow {r\cdot \text {id}_C} C$
(see [Reference Bühler6, Prop. 5.2]). So,
$C\xrightarrow {r\cdot \text {id}_C} C$
(see [Reference Bühler6, Prop. 5.2]). So,
![]() $[\gamma ]_{\cal{E}}=r\cdot [\sigma ]_{\cal{E}}=r\phi ([\sigma ]_{\cal{E}'})$
. Also,
$[\gamma ]_{\cal{E}}=r\cdot [\sigma ]_{\cal{E}}=r\phi ([\sigma ]_{\cal{E}'})$
. Also,
![]() $[\gamma ]_{\cal{E}}=\phi ([\gamma ]_{\cal{E}'})=\phi (r\cdot [\sigma ]_{\cal{E}'})$
. This shows that the natural inclusion map
$[\gamma ]_{\cal{E}}=\phi ([\gamma ]_{\cal{E}'})=\phi (r\cdot [\sigma ]_{\cal{E}'})$
. This shows that the natural inclusion map
![]() $\phi $
is R-linear.
$\phi $
is R-linear.
In the following corollary, we denote
![]() $\operatorname{Hom}_{\cal{A}}(-,-)$
just by
$\operatorname{Hom}_{\cal{A}}(-,-)$
just by
![]() $\operatorname{Hom}(-,-)$
(we completely ignore the subcategory, since all our subcategories are full). In view of Definition 4.10, and the discussion following 4.11, the following corollary is crucial for recovering [Reference Striuli35, Props. 1.37 and 1.38].
$\operatorname{Hom}(-,-)$
(we completely ignore the subcategory, since all our subcategories are full). In view of Definition 4.10, and the discussion following 4.11, the following corollary is crucial for recovering [Reference Striuli35, Props. 1.37 and 1.38].
Corollary 3.9. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $({\cal{A}}',{\cal{E}}')$
be a strictly full exact subcategory of
$({\cal{A}}',{\cal{E}}')$
be a strictly full exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
. Let
$({\cal{A}},{\cal{E}})$
. Let
be a kernel–cokernel pair in
![]() $\cal{E}'$
. Then, for every
$\cal{E}'$
. Then, for every
![]() $A\in {\cal{A}}'$
, we have the following commutative diagrams of long exact sequences:
$A\in {\cal{A}}'$
, we have the following commutative diagrams of long exact sequences:

and

Proof. We will only prove the covariant version (the first diagram above), since the proof of the contravariant version is given by the dual argument. In the first diagram above, the commutativity of the first two squares is obvious. Also, the commutativity of the last two squares follows directly from the proof of Proposition 3.8 (i.e.,
![]() ${\operatorname{Ext}}_{\cal{E}'}(-,-)$
is a subfunctor of
${\operatorname{Ext}}_{\cal{E}'}(-,-)$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)$
). So, it is enough to prove that the following square is commutative:
${\operatorname{Ext}}_{\cal{E}}(-,-)$
). So, it is enough to prove that the following square is commutative:

Now,
![]() $f(g)=[\gamma ]_{\cal{E}}$
, where
$f(g)=[\gamma ]_{\cal{E}}$
, where
![]() $\gamma $
is the pullback of
$\gamma $
is the pullback of
![]() $\sigma $
by g in
$\sigma $
by g in
![]() $\cal{E}$
and
$\cal{E}$
and
![]() $f^*(g)=[\alpha ]_{\cal{E}'}$
, where
$f^*(g)=[\alpha ]_{\cal{E}'}$
, where
![]() $\alpha $
is the pullback of
$\alpha $
is the pullback of
![]() $\sigma $
by g in
$\sigma $
by g in
![]() $\cal{E}'$
. Since
$\cal{E}'$
. Since
![]() $({\cal{A}}',{\cal{E}}')$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}')$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
, by [Reference Bühler6, Prop. 5.2], we get that
$({\cal{A}},{\cal{E}})$
, by [Reference Bühler6, Prop. 5.2], we get that
![]() $[\gamma ]_{\cal{E}}=[\alpha ]_{\cal{E}}$
. Also, by definition,
$[\gamma ]_{\cal{E}}=[\alpha ]_{\cal{E}}$
. Also, by definition,
![]() $\phi _{A,M}([\alpha ]_{\cal{E}'})=[\alpha ]_{\cal{E}}$
. Thus,
$\phi _{A,M}([\alpha ]_{\cal{E}'})=[\alpha ]_{\cal{E}}$
. Thus,
![]() $f(g)=\phi _{A,M}(f^*(g))$
, so the above square commutes.
$f(g)=\phi _{A,M}(f^*(g))$
, so the above square commutes.
Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\cal{A}'$
be a strictly full subcategory of
$\cal{A}'$
be a strictly full subcategory of
![]() $\cal{A}$
. If
$\cal{A}$
. If
![]() and
and
![]() are two kernel–cokernel pairs in
are two kernel–cokernel pairs in
![]() $\cal{E}$
belonging to the same class in
$\cal{E}$
belonging to the same class in
![]() ${\operatorname{Ext}}_{\cal{E}}(A_2,A_1)$
, then
${\operatorname{Ext}}_{\cal{E}}(A_2,A_1)$
, then
![]() $B\cong C$
(by short five lemma); hence,
$B\cong C$
(by short five lemma); hence,
![]() $B\in {\cal{A}}'$
if and only if
$B\in {\cal{A}}'$
if and only if
![]() $C\in {\cal{A}}'$
. Hence, for every
$C\in {\cal{A}}'$
. Hence, for every
![]() $M,N\in {\cal{A}}'$
, the collection
$M,N\in {\cal{A}}'$
, the collection
![]() $\{[\sigma ]_{\cal{E}}\in {\operatorname{Ext}}_{\cal{E}}(M,N) : \text {the middle object of } \sigma \text { is in } {\cal{A}}'\}$
is well defined.
$\{[\sigma ]_{\cal{E}}\in {\operatorname{Ext}}_{\cal{E}}(M,N) : \text {the middle object of } \sigma \text { is in } {\cal{A}}'\}$
is well defined.
Proposition 3.10. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\cal{A}'$
be a strictly full additive subcategory of
$\cal{A}'$
be a strictly full additive subcategory of
![]() $\cal{A}$
. For every
$\cal{A}$
. For every
![]() $M,N\in {\cal{A}}'$
, define
$M,N\in {\cal{A}}'$
, define
![]() $F(M,N):=\{[\sigma ]_{\cal{E}}\in {\operatorname{Ext}}_{\cal{E}}(M,N) : \text { the middle object of } \sigma \text { is in } {\cal{A}}'\}$
. If
$F(M,N):=\{[\sigma ]_{\cal{E}}\in {\operatorname{Ext}}_{\cal{E}}(M,N) : \text { the middle object of } \sigma \text { is in } {\cal{A}}'\}$
. If
![]() $F(-,-)$
is a subfunctor of
$F(-,-)$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
via the natural inclusion maps, then
${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
via the natural inclusion maps, then
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Proof. By Lemma 3.3, it is enough to show that the pullback (resp. pushout) in
![]() $\cal{A}$
of every
$\cal{A}$
of every
![]() $\cal{E}$
-deflation (resp. inflation) of sequences in
$\cal{E}$
-deflation (resp. inflation) of sequences in
![]() ${\cal{E}}|_{\cal{A}'}$
along every morphism in
${\cal{E}}|_{\cal{A}'}$
along every morphism in
![]() $\cal{A}'$
is again in
$\cal{A}'$
is again in
![]() $\cal{A}'$
. We will only prove the pullback case, since the proof of the pushout case can be given by a similar argument. Let
$\cal{A}'$
. We will only prove the pullback case, since the proof of the pushout case can be given by a similar argument. Let
be an admissible epic in
![]() $\cal{E}$
such that it is in
$\cal{E}$
such that it is in
![]() ${\cal{E}}|_{\cal{A}'}$
, which means that there exist a kernel–cokernel pair
${\cal{E}}|_{\cal{A}'}$
, which means that there exist a kernel–cokernel pair
in
![]() $\cal{E}$
such that
$\cal{E}$
such that
![]() $A, B,C\in {\cal{A}}'$
. Also, let
$A, B,C\in {\cal{A}}'$
. Also, let
![]() $B'\xrightarrow {f} C$
be a morphism in
$B'\xrightarrow {f} C$
be a morphism in
![]() $\cal{A}'$
. Then we have a map
$\cal{A}'$
. Then we have a map
![]() $f^*:{\operatorname{Ext}}_{\cal{E}}(C,A)\to {\operatorname{Ext}}_{\cal{E}}(B',A)$
defined as follows: for every
$f^*:{\operatorname{Ext}}_{\cal{E}}(C,A)\to {\operatorname{Ext}}_{\cal{E}}(B',A)$
defined as follows: for every
![]() $[\sigma ]_{\cal{E}} \in {\operatorname{Ext}}_{\cal{E}}(C,A)$
, a representative of
$[\sigma ]_{\cal{E}} \in {\operatorname{Ext}}_{\cal{E}}(C,A)$
, a representative of
![]() $f^*([\sigma ]_{\cal{E}})$
is the pullback of
$f^*([\sigma ]_{\cal{E}})$
is the pullback of
![]() $\sigma $
by f in
$\sigma $
by f in
![]() $({\cal{A}},{\cal{E}})$
. Now, by definition of
$({\cal{A}},{\cal{E}})$
. Now, by definition of
![]() $F(-,-)$
, it is clear that
$F(-,-)$
, it is clear that
![]() $F(M,N)\subseteq {\operatorname{Ext}}_{\cal{E}}(M,N)$
for any
$F(M,N)\subseteq {\operatorname{Ext}}_{\cal{E}}(M,N)$
for any
![]() $M,N\in {\cal{A}}'$
. Since
$M,N\in {\cal{A}}'$
. Since
![]() $F(-,-)$
is a subfunctor of
$F(-,-)$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
, we have the following commutative square:
${\operatorname{Ext}}_{\cal{E}}(-,-)|_{{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'}:{\cal{A}}^{\prime \operatorname{op}}\times {\cal{A}}'\to \mathbf {Ab}$
, we have the following commutative square:

where the columns are natural inclusion maps. So, for every
![]() $[\beta ]_{\cal{E}} \in F(C,A)$
, a representative of
$[\beta ]_{\cal{E}} \in F(C,A)$
, a representative of
![]() $\tilde {f}([\beta ]_{\cal{E}})$
is the pullback of
$\tilde {f}([\beta ]_{\cal{E}})$
is the pullback of
![]() $\beta $
by f in
$\beta $
by f in
![]() $({\cal{A}},{\cal{E}})$
. Now, consider the pullback of
$({\cal{A}},{\cal{E}})$
. Now, consider the pullback of
![]() $\gamma $
by f in
$\gamma $
by f in
![]() $({\cal{A}},{\cal{E}})$
as follows:
$({\cal{A}},{\cal{E}})$
as follows:

Now,
![]() $[\gamma ]_{\cal{E}}\in F(C,A)$
, so
$[\gamma ]_{\cal{E}}\in F(C,A)$
, so
![]() $\tilde {f}([\gamma ]_{\cal{E}})\in F(B',A)$
implies that
$\tilde {f}([\gamma ]_{\cal{E}})\in F(B',A)$
implies that
![]() $A'\in {\cal{A}}'$
. Hence, the pullback in
$A'\in {\cal{A}}'$
. Hence, the pullback in
![]() $\cal{A}$
of every
$\cal{A}$
of every
![]() $\cal{E}$
-deflation of sequences in
$\cal{E}$
-deflation of sequences in
![]() ${\cal{E}}|_{\cal{A}'}$
along every morphism in
${\cal{E}}|_{\cal{A}'}$
along every morphism in
![]() $\cal{A}'$
is again in
$\cal{A}'$
is again in
![]() $\cal{A}'$
. Hence, by Lemma 3.3, we get that
$\cal{A}'$
. Hence, by Lemma 3.3, we get that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
4 Subcategories and subfunctors of
 ${\operatorname{Ext}}^1$
from numerical functions and applications to module categories
${\operatorname{Ext}}^1$
from numerical functions and applications to module categories
In this section, we present tools to identify exact subcategories of an exact category coming from certain numerical functions. Consequently, due to Proposition 3.8, we are also able to identify subfunctors of
![]() ${\operatorname{Ext}}^1$
associated with certain numerical functions. Our first result in this direction is an application of Theorem 3.6.
${\operatorname{Ext}}^1$
associated with certain numerical functions. Our first result in this direction is an application of Theorem 3.6.
Proposition 4.1. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\phi :{\cal{A}}\to \mathbb {Z}_{\le 0}$
be a function such that
$\phi :{\cal{A}}\to \mathbb {Z}_{\le 0}$
be a function such that
![]() $\phi $
is constant on isomorphism classes of objects in
$\phi $
is constant on isomorphism classes of objects in
![]() $\cal{A}$
,
$\cal{A}$
,
![]() $\phi $
is additive on finite biproducts, and
$\phi $
is additive on finite biproducts, and
![]() $\phi $
is sub-additive on kernel–cokernel pairs in
$\phi $
is sub-additive on kernel–cokernel pairs in
![]() $\cal{E}$
(i.e., if
$\cal{E}$
(i.e., if
![]() is in
is in
![]() $\cal{E}$
, then
$\cal{E}$
, then
![]() $\phi (N)\le \phi (M)+\phi (L)$
). Let
$\phi (N)\le \phi (M)+\phi (L)$
). Let
![]() $\cal{A}'$
be the strictly full subcategory of
$\cal{A}'$
be the strictly full subcategory of
![]() $\cal{A}$
, whose objects are given by
$\cal{A}$
, whose objects are given by
![]() $\{M\in {\cal{A}}: \phi (M)=0\}$
. Then
$\{M\in {\cal{A}}: \phi (M)=0\}$
. Then
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Proof. Note that
![]() $\cal{A}'$
is a strict subcategory of
$\cal{A}'$
is a strict subcategory of
![]() $\cal{A}$
since
$\cal{A}$
since
![]() $\phi $
is constant on isomorphism classes of objects in
$\phi $
is constant on isomorphism classes of objects in
![]() $\cal{A}$
. Since
$\cal{A}$
. Since
![]() $\phi $
is additive on finite biproduct,
$\phi $
is additive on finite biproduct,
![]() $\phi (0_{\cal{A}})=\phi (0_{\cal{A}}\oplus 0_{\cal{A}})=\phi (0_{\cal{A}})+\phi (0_{\cal{A}})$
, and hence
$\phi (0_{\cal{A}})=\phi (0_{\cal{A}}\oplus 0_{\cal{A}})=\phi (0_{\cal{A}})+\phi (0_{\cal{A}})$
, and hence
![]() $\phi (0_{\cal{A}})=0$
. Hence,
$\phi (0_{\cal{A}})=0$
. Hence,
![]() $0_{\cal{A}}\in {\cal{A}}'$
. Since
$0_{\cal{A}}\in {\cal{A}}'$
. Since
![]() $\cal{A}$
is an additive category and
$\cal{A}$
is an additive category and
![]() $\phi $
is additive on finite biproducts, by definition of
$\phi $
is additive on finite biproducts, by definition of
![]() $\cal{A}'$
, we get that for every
$\cal{A}'$
, we get that for every
![]() $X,Y\in {\cal{A}}'$
, the biproduct of X and Y in
$X,Y\in {\cal{A}}'$
, the biproduct of X and Y in
![]() $\cal{A}$
also belongs to
$\cal{A}$
also belongs to
![]() $\cal{A}'$
. Hence,
$\cal{A}'$
. Hence,
![]() $\cal{A}'$
is an additive subcategory of
$\cal{A}'$
is an additive subcategory of
![]() $\cal{A}$
. Let
$\cal{A}$
. Let
![]() $B\in {\cal{A}}'$
and
$B\in {\cal{A}}'$
and
![]() be a kernel–cokernel pair in
be a kernel–cokernel pair in
![]() $\mathcal E$
. We will show that
$\mathcal E$
. We will show that
![]() $A_1, A_2 \in {\cal{A}}'$
. Since
$A_1, A_2 \in {\cal{A}}'$
. Since
![]() $\phi $
is subadditive on kernel–cokernel pairs in
$\phi $
is subadditive on kernel–cokernel pairs in
![]() $\cal{E}$
and
$\cal{E}$
and
![]() $B\in {\cal{A}}'$
, we get
$B\in {\cal{A}}'$
, we get
![]() $0=\phi (B)\leq \phi (A_1)+\phi (A_2)\le 0$
. Hence,
$0=\phi (B)\leq \phi (A_1)+\phi (A_2)\le 0$
. Hence,
![]() $\phi (A_1)+\phi (A_2)=0$
. Since we know
$\phi (A_1)+\phi (A_2)=0$
. Since we know
![]() $\phi $
always takes non-positive values, we get
$\phi $
always takes non-positive values, we get
![]() $\phi (A_1)=\phi (A_2)=0$
; hence,
$\phi (A_1)=\phi (A_2)=0$
; hence,
![]() $A_1,A_2\in {\cal{A}}'$
. Thus,
$A_1,A_2\in {\cal{A}}'$
. Thus,
![]() $\cal{A}'$
is closed under kernels and co-kernels of admissible epics and monics in
$\cal{A}'$
is closed under kernels and co-kernels of admissible epics and monics in
![]() $\cal{E}$
, respectively. Then, by Theorem 3.6, we get that
$\cal{E}$
, respectively. Then, by Theorem 3.6, we get that
![]() $({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
$({\cal{A}}',{\cal{E}}|_{\cal{A}'})$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
We now proceed to give our main example of Proposition 4.1. First, we recall some terminologies and prove some preliminary lemmas. For any unexpected concepts and notations, we refer the reader to [Reference Bruns and Herzog3] and [Reference Leuschke and Wiegand27].
Let R be a commutative ring, and let
![]() ${\cal{S}}_R$
be the collection of all short exact sequences of R-modules, which gives the standard exact structure on
${\cal{S}}_R$
be the collection of all short exact sequences of R-modules, which gives the standard exact structure on
![]() ${\operatorname{mod}}\ R$
. When the ring in question is clear, we drop the suffix R and write only
${\operatorname{mod}}\ R$
. When the ring in question is clear, we drop the suffix R and write only
![]() $\cal{S}$
. Note that since
$\cal{S}$
. Note that since
![]() ${\operatorname{mod}}\ R$
is extension closed in
${\operatorname{mod}}\ R$
is extension closed in
![]() ${\operatorname{mod}}\ R$
, the collection of all short exact sequences in
${\operatorname{mod}}\ R$
, the collection of all short exact sequences in
![]() ${\operatorname{mod}}\ R$
gives an exact subcategory of
${\operatorname{mod}}\ R$
gives an exact subcategory of
![]() ${\operatorname{mod}}\ R$
, and we take this as the standard exact structure of
${\operatorname{mod}}\ R$
, and we take this as the standard exact structure of
![]() ${\operatorname{mod}}\ R$
. Note that if
${\operatorname{mod}}\ R$
. Note that if
![]() $({\cal{X}},{\cal{E}})$
is an exact subcategory of
$({\cal{X}},{\cal{E}})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
and
${\operatorname{mod}}\ R$
and
![]() ${\cal{X}}\subseteq {\operatorname{mod}}\ R$
, then
${\cal{X}}\subseteq {\operatorname{mod}}\ R$
, then
![]() $({\cal{X}},{\cal{E}})$
is also an exact subcategory of
$({\cal{X}},{\cal{E}})$
is also an exact subcategory of
![]() ${\operatorname{mod}}\ R$
.
${\operatorname{mod}}\ R$
.
Now, for a Noetherian local ring
![]() $(R,\mathfrak {m})$
of dimension d and for an integer
$(R,\mathfrak {m})$
of dimension d and for an integer
![]() $s\ge 0$
, let
$s\ge 0$
, let
![]() $\operatorname{CM}^s(R)$
denote the full subcategory of
$\operatorname{CM}^s(R)$
denote the full subcategory of
![]() ${\operatorname{mod}}\ R$
consisting of the zero-module, and all Cohen–Macaulay R-modules [Reference Bruns and Herzog3, Def. 2.1.1] of dimension s. Note that when
${\operatorname{mod}}\ R$
consisting of the zero-module, and all Cohen–Macaulay R-modules [Reference Bruns and Herzog3, Def. 2.1.1] of dimension s. Note that when
![]() $s=d$
,
$s=d$
,
![]() $\operatorname{CM}^d(R)$
is just the category of all maximal Cohen–Macaulay modules, which we will also denote by
$\operatorname{CM}^d(R)$
is just the category of all maximal Cohen–Macaulay modules, which we will also denote by
![]() $\operatorname{CM}(R)$
.
$\operatorname{CM}(R)$
.
4.2. We quickly note that for each
![]() $s\ge 0$
,
$s\ge 0$
,
![]() $\operatorname{CM}^s(R)$
is closed under finite direct sums, direct summands, and closed under extensions in
$\operatorname{CM}^s(R)$
is closed under finite direct sums, direct summands, and closed under extensions in
![]() ${\operatorname{mod}}\ R$
. Indeed, let
${\operatorname{mod}}\ R$
. Indeed, let
![]() $0\to L \to M \to N \to 0$
be a short exact sequence with
$0\to L \to M \to N \to 0$
be a short exact sequence with
![]() $L,N\in \operatorname{CM}^s(R)$
. If L or N is zero, then there is nothing to prove. So, assume
$L,N\in \operatorname{CM}^s(R)$
. If L or N is zero, then there is nothing to prove. So, assume
![]() $L,N$
are nonzero. Now,
$L,N$
are nonzero. Now,
![]() $M\in {\operatorname{mod}}\ R$
, and we also have the following calculation for
$M\in {\operatorname{mod}}\ R$
, and we also have the following calculation for
![]() $\dim M$
:
$\dim M$
:
 $\dim M = \dim \operatorname{Supp}(M)=\dim \left (\operatorname{Supp}(L)\cup \operatorname{Supp}(N)\right )=\max \{\dim \operatorname{Supp}(L),\dim \operatorname{Supp}(N)\}=\max \{\dim L, \dim N\}=s$
. Consequently,
$\dim M = \dim \operatorname{Supp}(M)=\dim \left (\operatorname{Supp}(L)\cup \operatorname{Supp}(N)\right )=\max \{\dim \operatorname{Supp}(L),\dim \operatorname{Supp}(N)\}=\max \{\dim L, \dim N\}=s$
. Consequently,
![]() $s=\inf \{\operatorname{depth}_R L, \operatorname{depth}_R N\}\le \operatorname{depth}_R M \le \dim M=s$
, which shows
$s=\inf \{\operatorname{depth}_R L, \operatorname{depth}_R N\}\le \operatorname{depth}_R M \le \dim M=s$
, which shows
![]() $M\in \operatorname{CM}^s(R)$
. Thus,
$M\in \operatorname{CM}^s(R)$
. Thus,
![]() $\operatorname{CM}^s(R)$
is closed under extensions in
$\operatorname{CM}^s(R)$
is closed under extensions in
![]() ${\operatorname{mod}}\ R$
. To also show
${\operatorname{mod}}\ R$
. To also show
![]() $\operatorname{CM}^s(R)$
is closed under direct summands, let
$\operatorname{CM}^s(R)$
is closed under direct summands, let
![]() $M,N$
be nonzero modules with
$M,N$
be nonzero modules with
![]() $M\oplus N\in \operatorname{CM}^s(R)$
. Then,
$M\oplus N\in \operatorname{CM}^s(R)$
. Then,
![]() $M,N\in {\operatorname{mod}}\ R$
, and
$M,N\in {\operatorname{mod}}\ R$
, and
![]() $s=\operatorname{depth}_R(M\oplus N)=\inf \{\operatorname{depth}_R M,\operatorname{depth}_R N\}\le \operatorname{depth}_R M\le \dim M\le \dim (M\oplus N)=s$
, and thus
$s=\operatorname{depth}_R(M\oplus N)=\inf \{\operatorname{depth}_R M,\operatorname{depth}_R N\}\le \operatorname{depth}_R M\le \dim M\le \dim (M\oplus N)=s$
, and thus
![]() $M\in \operatorname{CM}^s(R)$
.
$M\in \operatorname{CM}^s(R)$
.
Hence, if
![]() $\cal{S}$
is the standard exact structure on
$\cal{S}$
is the standard exact structure on
![]() ${\operatorname{mod}}\ R$
, then
${\operatorname{mod}}\ R$
, then
![]() $(\operatorname{CM}^s(R),{\cal{S}}|_{\operatorname{CM}^s(R)})$
is an exact subcategory of
$(\operatorname{CM}^s(R),{\cal{S}}|_{\operatorname{CM}^s(R)})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
by Proposition 3.5. Now, let I be an
${\operatorname{mod}}\ R$
by Proposition 3.5. Now, let I be an
![]() $\mathfrak {m}$
-primary ideal and let
$\mathfrak {m}$
-primary ideal and let
![]() $\phi _I:\operatorname{CM}^s(R)\to \mathbb Z$
be the function defined by
$\phi _I:\operatorname{CM}^s(R)\to \mathbb Z$
be the function defined by
![]() $\phi _I(M):=\lambda _R(M/IM)-e_R(I,M)$
, where
$\phi _I(M):=\lambda _R(M/IM)-e_R(I,M)$
, where
![]() $e_R(I,M)$
is the multiplicity of M with respect to I (see [Reference Bruns and Herzog3, Def. 4.6.1]). We first show that
$e_R(I,M)$
is the multiplicity of M with respect to I (see [Reference Bruns and Herzog3, Def. 4.6.1]). We first show that
![]() $\phi _I$
satisfy all the hypothesis of Proposition 4.1. To prove this, we will need to pass to the faithfully flat extension
$\phi _I$
satisfy all the hypothesis of Proposition 4.1. To prove this, we will need to pass to the faithfully flat extension
![]() $S=R[X]_{\mathfrak {m}[X]}$
whose unique maximal ideal is
$S=R[X]_{\mathfrak {m}[X]}$
whose unique maximal ideal is
![]() $\mathfrak {m} S$
. That we can harmlessly pass to this extension, is discussed in the following.
$\mathfrak {m} S$
. That we can harmlessly pass to this extension, is discussed in the following.
4.3. Let
![]() $(R,\mathfrak {m})$
be a local ring, and consider
$(R,\mathfrak {m})$
be a local ring, and consider
![]() $S=R[X]_{\mathfrak {m}[X]}$
, which is a faithfully flat extension of R and the unique maximal ideal of S is
$S=R[X]_{\mathfrak {m}[X]}$
, which is a faithfully flat extension of R and the unique maximal ideal of S is
![]() $\mathfrak {m} S$
, whose residue field
$\mathfrak {m} S$
, whose residue field
![]() $S/\mathfrak {m} S$
is infinite (see [Reference Huneke and Swanson24, §8.4]). Let
$S/\mathfrak {m} S$
is infinite (see [Reference Huneke and Swanson24, §8.4]). Let
![]() $M\in {\operatorname{mod}} (R)$
. By [Reference Bruns and Herzog3, Th. 2.1.7] (and the sentences following it), we have
$M\in {\operatorname{mod}} (R)$
. By [Reference Bruns and Herzog3, Th. 2.1.7] (and the sentences following it), we have
![]() $M\in \operatorname{CM}^s(R)$
if and only if
$M\in \operatorname{CM}^s(R)$
if and only if
![]() $M\otimes _R S \in \operatorname{CM}^s(S)$
. Let I be an
$M\otimes _R S \in \operatorname{CM}^s(S)$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal of R. As
$\mathfrak {m}$
-primary ideal of R. As
![]() $\mathfrak {m} S$
is the maximal ideal of S, so
$\mathfrak {m} S$
is the maximal ideal of S, so
![]() $IS=I\otimes _R S$
is also primary to the maximal ideal of S. Now,
$IS=I\otimes _R S$
is also primary to the maximal ideal of S. Now,
 $S\otimes _R \dfrac {M}{IM}\cong \dfrac {S\otimes _R M}{S\otimes _R (IM)}=\dfrac {S\otimes _R M}{(IS)(S\otimes _R M)}$
by Lemma 5.2.5(1). Hence,
$S\otimes _R \dfrac {M}{IM}\cong \dfrac {S\otimes _R M}{S\otimes _R (IM)}=\dfrac {S\otimes _R M}{(IS)(S\otimes _R M)}$
by Lemma 5.2.5(1). Hence,
 $\lambda _S\left (\dfrac {S\otimes _R M}{(IS)(S\otimes _R M)}\right )=\lambda _S\left (S\otimes _R \dfrac {M}{IM} \right )=\lambda _R\left (\dfrac {M}{IM}\right )$
, where the last equality is by [38, Tag 02M1] remembering that
$\lambda _S\left (\dfrac {S\otimes _R M}{(IS)(S\otimes _R M)}\right )=\lambda _S\left (S\otimes _R \dfrac {M}{IM} \right )=\lambda _R\left (\dfrac {M}{IM}\right )$
, where the last equality is by [38, Tag 02M1] remembering that
![]() $S/\mathfrak {m} S$
is the residue field of S. Also,
$S/\mathfrak {m} S$
is the residue field of S. Also,
 $e_R(I,M):=\lim _{n\to \infty }\dfrac {(\dim M)!}{n^{\dim M}}\lambda _R\left (\dfrac {M}{I^{n+1}M}\right )$
, and
$e_R(I,M):=\lim _{n\to \infty }\dfrac {(\dim M)!}{n^{\dim M}}\lambda _R\left (\dfrac {M}{I^{n+1}M}\right )$
, and
![]() $\dim _S(M\otimes _R S)=\dim _R(M)$
[Reference Bruns and Herzog3, Th. A.11(b)], so a similar argument as the previous one shows
$\dim _S(M\otimes _R S)=\dim _R(M)$
[Reference Bruns and Herzog3, Th. A.11(b)], so a similar argument as the previous one shows
![]() $e_R(I,M)=e_S(IS, S\otimes _R M)$
. Thus,
$e_R(I,M)=e_S(IS, S\otimes _R M)$
. Thus,
![]() $\phi _I(M)=\phi _{IS}(S\otimes _R M)$
.
$\phi _I(M)=\phi _{IS}(S\otimes _R M)$
.
Lemma 4.4. The function
![]() $\phi _I:\operatorname{CM}^s(R)\to \mathbb Z$
satisfies
$\phi _I:\operatorname{CM}^s(R)\to \mathbb Z$
satisfies
![]() $\phi _I(M)\le 0$
, is constant on isomorphism classes of modules in
$\phi _I(M)\le 0$
, is constant on isomorphism classes of modules in
![]() $\operatorname{CM}^s(R)$
, additive on finite biproducts, and subadditive on short exact sequences of modules in
$\operatorname{CM}^s(R)$
, additive on finite biproducts, and subadditive on short exact sequences of modules in
![]() $\operatorname{CM}^s(R)$
.
$\operatorname{CM}^s(R)$
.
Proof. It is obvious that
![]() $\phi _I$
is constant on isomorphism classes of modules in
$\phi _I$
is constant on isomorphism classes of modules in
![]() $\operatorname{CM}^s(R)$
, and additive on finite biproducts (direct sums). Now,
$\operatorname{CM}^s(R)$
, and additive on finite biproducts (direct sums). Now,
![]() $e_R(I,-)$
is additive on short exact sequences of modules in
$e_R(I,-)$
is additive on short exact sequences of modules in
![]() $\operatorname{CM}^s(R)$
by [Reference Bruns and Herzog3, Cor. 4.7.7]. Since
$\operatorname{CM}^s(R)$
by [Reference Bruns and Herzog3, Cor. 4.7.7]. Since
![]() $\lambda _R((-)\otimes _R R/I)$
is always subadditive on short exact sequences, this proves
$\lambda _R((-)\otimes _R R/I)$
is always subadditive on short exact sequences, this proves
![]() $\phi _I$
is also subadditive on short exact sequences of modules in
$\phi _I$
is also subadditive on short exact sequences of modules in
![]() $\operatorname{CM}^s(R)$
. Now, we finally prove that
$\operatorname{CM}^s(R)$
. Now, we finally prove that
![]() $\phi _I(M)\le 0$
for all
$\phi _I(M)\le 0$
for all
![]() $M\in \operatorname{CM}^s(R)$
. If
$M\in \operatorname{CM}^s(R)$
. If
![]() $\dim M=0$
, then
$\dim M=0$
, then
![]() $e_R(I,M)=\lambda _R(M)\ge \lambda _R(M/IM)$
, so
$e_R(I,M)=\lambda _R(M)\ge \lambda _R(M/IM)$
, so
![]() $\phi _I(M)\le 0$
. Now, assume that
$\phi _I(M)\le 0$
. Now, assume that
![]() $s=\dim M>0$
. We may assume that R has infinite residue field due to 4.3. By [Reference Bruns and Herzog3, Cor. 4.6.10], we have
$s=\dim M>0$
. We may assume that R has infinite residue field due to 4.3. By [Reference Bruns and Herzog3, Cor. 4.6.10], we have
![]() $e_R(I,M)=e_R((\mathbf x),M)$
for some system of parameters
$e_R(I,M)=e_R((\mathbf x),M)$
for some system of parameters
![]() $\mathbf x=x_1,...,x_s$
on M, which is a reduction of I with respect to M. Then,
$\mathbf x=x_1,...,x_s$
on M, which is a reduction of I with respect to M. Then,
![]() $\mathbf x$
is an M-regular sequence, since M is Cohen–Macaulay (see [Reference Bruns and Herzog3, Th. 2.1.2(d)]). Let
$\mathbf x$
is an M-regular sequence, since M is Cohen–Macaulay (see [Reference Bruns and Herzog3, Th. 2.1.2(d)]). Let
![]() $J=(\mathbf x)$
. Since
$J=(\mathbf x)$
. Since
![]() $\mathbf x$
is an M-regular sequence, by [Reference Bruns and Herzog3, Th. 1.1.8], we have
$\mathbf x$
is an M-regular sequence, by [Reference Bruns and Herzog3, Th. 1.1.8], we have
 $J^nM/J^{n+1}M\cong (M/JM)^{\oplus \dfrac {(s+n-1)!}{n!(s-1)!}}$
. Hence,
$J^nM/J^{n+1}M\cong (M/JM)^{\oplus \dfrac {(s+n-1)!}{n!(s-1)!}}$
. Hence,
 $e_R(I,M)=e_R(J,M)=(s-1)!\lim _{n\to \infty }\dfrac {\lambda _R(J^nM/J^{n+1}M)}{n^{s-1}}=\lambda _R(M/JM)\ge \lambda _R(M/I M)$
(the last inequality follows by noticing that
$e_R(I,M)=e_R(J,M)=(s-1)!\lim _{n\to \infty }\dfrac {\lambda _R(J^nM/J^{n+1}M)}{n^{s-1}}=\lambda _R(M/JM)\ge \lambda _R(M/I M)$
(the last inequality follows by noticing that
![]() $J\subseteq I$
). Hence,
$J\subseteq I$
). Hence,
![]() $\phi _I(M)\le 0$
.
$\phi _I(M)\le 0$
.
Definition 4.5. Let
![]() $(R,\mathfrak {m})$
be a Noetherian local ring, and let I be an
$(R,\mathfrak {m})$
be a Noetherian local ring, and let I be an
![]() $\mathfrak {m}$
-primary ideal. Let
$\mathfrak {m}$
-primary ideal. Let
![]() $s\ge 0$
be an integer. We denote by
$s\ge 0$
be an integer. We denote by
![]() $\operatorname{Ul}^s_I(R)$
the full subcategory of all modules
$\operatorname{Ul}^s_I(R)$
the full subcategory of all modules
![]() $M\in \operatorname{CM}^s(R)$
such that
$M\in \operatorname{CM}^s(R)$
such that
![]() $\phi _I(M)=0$
, that is,
$\phi _I(M)=0$
, that is,
![]() $\lambda _R(M/IM)=e_R(I,M)$
. When
$\lambda _R(M/IM)=e_R(I,M)$
. When
![]() $s=\dim R$
, we will denote this subcategory simply by
$s=\dim R$
, we will denote this subcategory simply by
![]() $\operatorname{Ul}_I(R)$
. When
$\operatorname{Ul}_I(R)$
. When
![]() $I=\mathfrak {m}$
,
$I=\mathfrak {m}$
,
![]() $\operatorname{Ul}^s_{\mathfrak {m}}(R)$
will be denoted by
$\operatorname{Ul}^s_{\mathfrak {m}}(R)$
will be denoted by
![]() $\operatorname{Ul}^s(R)$
. We will also denote
$\operatorname{Ul}^s(R)$
. We will also denote
![]() $\operatorname{Ul}^{\dim R}_{\mathfrak {m}}(R)$
simply by
$\operatorname{Ul}^{\dim R}_{\mathfrak {m}}(R)$
simply by
![]() $\operatorname{Ul}(R)$
. Note that when
$\operatorname{Ul}(R)$
. Note that when
![]() $s=\dim R=1$
and R is Cohen–Macaulay,
$s=\dim R=1$
and R is Cohen–Macaulay,
![]() $\operatorname{Ul}_I(R)$
is exactly the collection of all I-Ulrich modules as defined in [Reference Dao, Maitra and Sridhar11, Def. 4.1].
$\operatorname{Ul}_I(R)$
is exactly the collection of all I-Ulrich modules as defined in [Reference Dao, Maitra and Sridhar11, Def. 4.1].
Remark 4.6. In terms of [Reference Goto, Takahashi and Taniguchi21, Def. 2.1], a nonzero R-module M is Ulrich if
![]() $M\in \operatorname{Ul}^s(R)$
for some
$M\in \operatorname{Ul}^s(R)$
for some
![]() $s\ge 0$
in our notation. When R is Cohen–Macaulay, then the modules in
$s\ge 0$
in our notation. When R is Cohen–Macaulay, then the modules in
![]() $\operatorname{Ul}(R)$
are simply the maximally generated modules as studied in [Reference Brennan, Herzog and Ulrich2].
$\operatorname{Ul}(R)$
are simply the maximally generated modules as studied in [Reference Brennan, Herzog and Ulrich2].
Corollary 4.7. For each integer
![]() $s\ge 0$
and
$s\ge 0$
and
![]() $\mathfrak {m}$
-primary ideal I,
$\mathfrak {m}$
-primary ideal I,
![]() $(\operatorname{Ul}^s_I(R), {\cal{S}}|_{{\operatorname{Ul}}^s_I(R)})$
is an exact subcategory of
$(\operatorname{Ul}^s_I(R), {\cal{S}}|_{{\operatorname{Ul}}^s_I(R)})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
(hence of
${\operatorname{mod}}\ R$
(hence of
![]() ${\operatorname{mod}}\ R$
). Hence,
${\operatorname{mod}}\ R$
). Hence,
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(-,-): \operatorname{Ul}^s_I(R)^{op}\times \operatorname{Ul}^s_I(R)\to {\operatorname{mod}}\ R$
is a subfunctor of
${\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(-,-): \operatorname{Ul}^s_I(R)^{op}\times \operatorname{Ul}^s_I(R)\to {\operatorname{mod}}\ R$
is a subfunctor of
![]() ${\operatorname{Ext}}^1_{R}(-,-): \operatorname{Ul}^s_I(R)^{op}\times \operatorname{Ul}^s_I(R)\to {\operatorname{mod}}\ R$
.
${\operatorname{Ext}}^1_{R}(-,-): \operatorname{Ul}^s_I(R)^{op}\times \operatorname{Ul}^s_I(R)\to {\operatorname{mod}}\ R$
.
Proof. Since it has been noticed that
![]() $(\operatorname{CM}^s(R),{\cal{S}}|_{\operatorname{CM}^s(R)})$
is an exact subcategory of
$(\operatorname{CM}^s(R),{\cal{S}}|_{\operatorname{CM}^s(R)})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
, by Lemma 4.4 and Proposition 4.1, it follows that
${\operatorname{mod}}\ R$
, by Lemma 4.4 and Proposition 4.1, it follows that
![]() $(\operatorname{Ul}^s_I(R), {\cal{S}}|_{\operatorname{Ul}^s_I(R)})$
is an exact subcategory of
$(\operatorname{Ul}^s_I(R), {\cal{S}}|_{\operatorname{Ul}^s_I(R)})$
is an exact subcategory of
![]() $(\operatorname{CM}^s(R),{\cal{S}}|_{\operatorname{CM}^s(R)})$
, and hence of
$(\operatorname{CM}^s(R),{\cal{S}}|_{\operatorname{CM}^s(R)})$
, and hence of
![]() ${\operatorname{mod}}\ R$
. The subfunctor part now follows from Proposition 3.8.
${\operatorname{mod}}\ R$
. The subfunctor part now follows from Proposition 3.8.
Next, we record a proposition for constructing a special kind of exact substructure of an exact structure
![]() $\cal{E}$
on a category
$\cal{E}$
on a category
![]() $\cal{A}$
, without shrinking the category, that also comes from certain kinds of numerical functions. This is used in the next section to recover and improve some results on module categories.
$\cal{A}$
, without shrinking the category, that also comes from certain kinds of numerical functions. This is used in the next section to recover and improve some results on module categories.
Theorem 4.8. Let
![]() $({\cal{A}},{\cal{E}})$
be an exact category. Let
$({\cal{A}},{\cal{E}})$
be an exact category. Let
![]() $\phi :{\cal{A}} \to \mathbb Z$
be a function such that
$\phi :{\cal{A}} \to \mathbb Z$
be a function such that
![]() $\phi $
is constant on isomorphism classes of objects in
$\phi $
is constant on isomorphism classes of objects in
![]() $\cal{A}$
,
$\cal{A}$
,
![]() $\phi $
is additive on finite biproducts, and
$\phi $
is additive on finite biproducts, and
![]() $\phi $
is subadditive on kernel–cokernel pairs in
$\phi $
is subadditive on kernel–cokernel pairs in
![]() $\cal{E}$
(i.e., if
$\cal{E}$
(i.e., if
![]() is in
is in
![]() $\cal{E}$
, then
$\cal{E}$
, then
![]() $\phi (N)\le \phi (M)+\phi (L)$
). Set
$\phi (N)\le \phi (M)+\phi (L)$
). Set
![]() ${\cal{E}}^{\phi }:=\{\text {kernel--cokernel pairs in } {\cal{E}} \text { on which } \phi \text { is additive} \}$
. Then,
${\cal{E}}^{\phi }:=\{\text {kernel--cokernel pairs in } {\cal{E}} \text { on which } \phi \text { is additive} \}$
. Then,
![]() $({\cal{A}},{\cal{E}}^{\phi })$
is an exact subcategory of
$({\cal{A}},{\cal{E}}^{\phi })$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Proof. By [Reference Bühler6, Def. 2.1] and [Reference Bühler6, Rem. 2.4], it is enough to show that
![]() ${\cal{E}}^{\phi }$
is closed under isomorphisms and
${\cal{E}}^{\phi }$
is closed under isomorphisms and
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axioms [E0], [E0
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axioms [E0], [E0
![]() $^{\text {op}}$
], [E1
$^{\text {op}}$
], [E1
![]() $^{\text {op}}$
], [E2], and [E2
$^{\text {op}}$
], [E2], and [E2
![]() $^{\text {op}}$
]. First, we will show that
$^{\text {op}}$
]. First, we will show that
![]() ${\cal{E}}^{\phi }$
is closed under isomorphisms. Let
${\cal{E}}^{\phi }$
is closed under isomorphisms. Let
![]() be a kernel–cokernel pair in
be a kernel–cokernel pair in
![]() ${\cal{E}}^{\phi }$
. Also, let
${\cal{E}}^{\phi }$
. Also, let
![]() $M'\to N'\to L'$
be a kernel–cokernel pair in
$M'\to N'\to L'$
be a kernel–cokernel pair in
![]() $\cal{A}$
such that it is isomorphic to
$\cal{A}$
such that it is isomorphic to
![]() , which implies that
, which implies that
![]() is in
is in
![]() $\cal{E}$
and
$\cal{E}$
and
![]() $M\cong M'$
,
$M\cong M'$
,
![]() $N\cong N'$
,
$N\cong N'$
,
![]() $L\cong L'$
. Since
$L\cong L'$
. Since
![]() $\phi (N)=\phi (M)+\phi (L)$
and
$\phi (N)=\phi (M)+\phi (L)$
and
![]() $\phi $
is constant on isomorphism classes of objects in
$\phi $
is constant on isomorphism classes of objects in
![]() $\cal{A}$
, we have
$\cal{A}$
, we have
![]() $\phi (N')=\phi (N)=\phi (M)+\phi (L)=\phi (M')+\phi (L')$
. So,
$\phi (N')=\phi (N)=\phi (M)+\phi (L)=\phi (M')+\phi (L')$
. So,
![]() is in
is in
![]() ${\cal{E}}^{\phi }$
. Hence,
${\cal{E}}^{\phi }$
. Hence,
![]() ${\cal{E}}^{\phi }$
is closed under isomorphisms. Next, we will show that
${\cal{E}}^{\phi }$
is closed under isomorphisms. Next, we will show that
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0]. Let
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0]. Let
![]() $A\in {\cal{A}}$
. Since
$A\in {\cal{A}}$
. Since
![]() $({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
$({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
![]() is in
is in
![]() $\cal{E}$
. Since
$\cal{E}$
. Since
![]() $\phi $
is additive on finite biproducts,
$\phi $
is additive on finite biproducts,
![]() $\phi $
is additive on the kernel–cokernel pair
$\phi $
is additive on the kernel–cokernel pair
![]() . Hence, by definition,
. Hence, by definition,
![]() is in
is in
![]() ${\cal{E}}^{\phi }$
, which implies that
${\cal{E}}^{\phi }$
, which implies that
![]() $1_A$
is an admissible monic in
$1_A$
is an admissible monic in
![]() ${\cal{E}}^{\phi }$
. So,
${\cal{E}}^{\phi }$
. So,
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0]. Next, we will show that
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0]. Next, we will show that
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0
![]() $^{\text {op}}$
]. Let
$^{\text {op}}$
]. Let
![]() $A\in {\cal{A}}$
. Since
$A\in {\cal{A}}$
. Since
![]() $({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
$({\cal{A}},{\cal{E}})$
is an exact category, by [Reference Bühler6, Lem. 2.7], we get that
![]() is in
is in
![]() $\cal{E}$
. Since
$\cal{E}$
. Since
![]() $\phi $
is additive on finite biproducts,
$\phi $
is additive on finite biproducts,
![]() $\phi $
is additive on the kernel–cokernel pair
$\phi $
is additive on the kernel–cokernel pair
![]() . Hence, by definition,
. Hence, by definition,
![]() is in
is in
![]() ${\cal{E}}^{\phi }$
, which implies that
${\cal{E}}^{\phi }$
, which implies that
![]() $1_A$
is an admissible epic in
$1_A$
is an admissible epic in
![]() ${\cal{E}}^{\phi }$
. So,
${\cal{E}}^{\phi }$
. So,
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E0
![]() $^{\text {op}}$
]. Next, we will show that
$^{\text {op}}$
]. Next, we will show that
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E1
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E1
![]() $^{\text {op}}$
]. Let
$^{\text {op}}$
]. Let
![]() and
and
![]() be two admissible epics in
be two admissible epics in
![]() ${\cal{E}}^{\phi }$
. Then we will show that
${\cal{E}}^{\phi }$
. Then we will show that
![]() is an admissible epic in
is an admissible epic in
![]() ${\cal{E}}^{\phi }$
. Let
${\cal{E}}^{\phi }$
. Let
![]() be the complete kernel–cokernel pair of p, and consider a pullback square as in Proposition 3.4. From Proposition 3.4, we get that
be the complete kernel–cokernel pair of p, and consider a pullback square as in Proposition 3.4. From Proposition 3.4, we get that
![]() is a kernel–cokernel pair in
is a kernel–cokernel pair in
![]() $\cal{E}$
, so
$\cal{E}$
, so
![]() $\phi (B')\leq \phi (C)+\phi (A')$
.
$\phi (B')\leq \phi (C)+\phi (A')$
.
Now, consider the pullback square of Proposition 3.4

By the dual (pullback version) of [Reference Bühler6, Prop. 2.12(i)
![]() $\Rightarrow$
(iv)] we get a commutative diagram in
$\Rightarrow$
(iv)] we get a commutative diagram in
![]() $\cal{E}$
as follows:
$\cal{E}$
as follows:

The top row gives
![]() $\phi (A')\leq \phi (A)+\phi (D)$
. Thus,
$\phi (A')\leq \phi (A)+\phi (D)$
. Thus,
![]() $\phi (C)+\phi (A')\leq \phi (A)+\phi (C)+\phi (D)$
. Since
$\phi (C)+\phi (A')\leq \phi (A)+\phi (C)+\phi (D)$
. Since
![]() is an admissible epic in
is an admissible epic in
![]() ${\cal{E}}^{\phi }$
and
${\cal{E}}^{\phi }$
and
![]() is in
is in
![]() $\cal{E}$
and
$\cal{E}$
and
![]() $\phi (-)$
is constant on isomorphism classes of objects, we have
$\phi (-)$
is constant on isomorphism classes of objects, we have
![]() $\phi (A)+\phi (C)=\phi (B)$
. Thus,
$\phi (A)+\phi (C)=\phi (B)$
. Thus,
![]() $\phi (C)+\phi (A')\leq \phi (A)+\phi (C)+\phi (D)$
implies
$\phi (C)+\phi (A')\leq \phi (A)+\phi (C)+\phi (D)$
implies
![]() $\phi (C)+\phi (A')\leq \phi (B)+\phi (D)$
. Since
$\phi (C)+\phi (A')\leq \phi (B)+\phi (D)$
. Since
![]() is an admissible epic in
is an admissible epic in
![]() ${\cal{E}}^{\phi }$
, the bottom row of the above diagram gives
${\cal{E}}^{\phi }$
, the bottom row of the above diagram gives
![]() $\phi (B')=\phi (B)+\phi (D)$
. Hence,
$\phi (B')=\phi (B)+\phi (D)$
. Hence,
![]() $\phi (C)+\phi (A')\leq \phi (B')$
. Thus,
$\phi (C)+\phi (A')\leq \phi (B')$
. Thus,
![]() in
in
![]() $\cal{E}$
is actually in
$\cal{E}$
is actually in
![]() ${\cal{E}}^{\phi }$
. This shows
${\cal{E}}^{\phi }$
. This shows
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E1
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E1
![]() $^{\text {op}}$
].
$^{\text {op}}$
].
Now, we will show that
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E2]. Let
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E2]. Let
be an admissible monic in
![]() ${\cal{E}}^{\phi }$
, and let
${\cal{E}}^{\phi }$
, and let
![]() $A\xrightarrow {f}A'$
be an arbitrary morphism in
$A\xrightarrow {f}A'$
be an arbitrary morphism in
![]() $\cal{A}$
. Then we have the following pushout commutative square in
$\cal{A}$
. Then we have the following pushout commutative square in
![]() $\cal{E}$
:
$\cal{E}$
:

Then, by [Reference Bühler6, Prop. 2.12(ii)], we have the following kernel–cokernel pair in
![]() $\cal{E}$
:
$\cal{E}$
:
, so
![]() $\phi (B)+\phi (A')=\phi (B\oplus A')\leq \phi (A)+\phi (B')$
. Also, by [Reference Bühler6, Prop. 2.12(iv)], we have the following commutative diagram with rows being kernel–cokernel pairs in
$\phi (B)+\phi (A')=\phi (B\oplus A')\leq \phi (A)+\phi (B')$
. Also, by [Reference Bühler6, Prop. 2.12(iv)], we have the following commutative diagram with rows being kernel–cokernel pairs in
![]() $\cal{E}$
:
$\cal{E}$
:

Since
is an admissible monic in
![]() ${\cal{E}}^{\phi }$
, we have
${\cal{E}}^{\phi }$
, we have
![]() $\phi (B)=\phi (A)+\phi (C)$
. This implies
$\phi (B)=\phi (A)+\phi (C)$
. This implies
![]() $\phi (A)+\phi (C)+\phi (A')\leq \phi (A)+\phi (B')$
, so
$\phi (A)+\phi (C)+\phi (A')\leq \phi (A)+\phi (B')$
, so
![]() $\phi (C)+\phi (A')\leq \phi (B')$
. Also,
$\phi (C)+\phi (A')\leq \phi (B')$
. Also,
is a kernel–cokernel pair in
![]() $\cal{E}$
, so
$\cal{E}$
, so
![]() $\phi (B')\leq \phi (C)+\phi (A')$
. Thus,
$\phi (B')\leq \phi (C)+\phi (A')$
. Thus,
![]() $\phi (C)+\phi (A')=\phi (B')$
. Hence,
$\phi (C)+\phi (A')=\phi (B')$
. Hence,
is a kernel–cokernel pair in
![]() ${\cal{E}}^{\phi }$
, so
${\cal{E}}^{\phi }$
, so
is an admissible monic in
![]() ${\cal{E}}^{\phi }$
. Thus,
${\cal{E}}^{\phi }$
. Thus,
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E2]. A dual argument will show that
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E2]. A dual argument will show that
![]() $({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E2
$({\cal{A}},{\cal{E}}^{\phi })$
satisfies the axiom [E2
![]() $^{\text {op}}$
]. Hence,
$^{\text {op}}$
]. Hence,
![]() $({\cal{A}},{\cal{E}}^{\phi })$
is an exact subcategory of
$({\cal{A}},{\cal{E}}^{\phi })$
is an exact subcategory of
![]() $({\cal{A}},{\cal{E}})$
.
$({\cal{A}},{\cal{E}})$
.
Moving forward, we record some applications of Theorem 4.8.
4.9. Let
![]() $\cal{X}$
be a subcategory of
$\cal{X}$
be a subcategory of
![]() ${\operatorname{Mod}} (R)$
such that
${\operatorname{Mod}} (R)$
such that
![]() $({\cal{X}},{\cal{S}}|_{\cal{X}})$
is an exact subcategory of
$({\cal{X}},{\cal{S}}|_{\cal{X}})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. In this case, for
${\operatorname{mod}}\ R$
. In this case, for
![]() $M,N\in {\cal{X}}$
, by
$M,N\in {\cal{X}}$
, by
![]() ${\operatorname{Ext}}^1_{\cal{X}}(M,N)$
, we will mean
${\operatorname{Ext}}^1_{\cal{X}}(M,N)$
, we will mean
![]() ${\operatorname{Ext}}_{{\cal{S}}|_{\cal{X}}}(M,N)$
, that is,
${\operatorname{Ext}}_{{\cal{S}}|_{\cal{X}}}(M,N)$
, that is,
![]() ${\operatorname{Ext}}^1_{\cal{X}}(M,N)=\{[\sigma ]: \text {the middle object of }\sigma \text { is in } {\cal{X}}\}$
. (Note that it does not matter whether the equivalence class is taken in
${\operatorname{Ext}}^1_{\cal{X}}(M,N)=\{[\sigma ]: \text {the middle object of }\sigma \text { is in } {\cal{X}}\}$
. (Note that it does not matter whether the equivalence class is taken in
![]() ${\cal{S}}|_{\cal{X}}$
or
${\cal{S}}|_{\cal{X}}$
or
![]() $\cal{S}$
by Remark 3.7.) Note that
$\cal{S}$
by Remark 3.7.) Note that
![]() ${\operatorname{Ext}}^1_{\cal{X}}(-,-): {\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
is a subfunctor of
${\operatorname{Ext}}^1_{\cal{X}}(-,-): {\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
is a subfunctor of
![]() ${\operatorname{Ext}}^1_R(-,-): {\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
by Proposition 3.8. For example, we can apply this discussion to
${\operatorname{Ext}}^1_R(-,-): {\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
by Proposition 3.8. For example, we can apply this discussion to
![]() ${\cal{X}}=\operatorname{Ul}^s_I(R)$
due to Corollary 4.7.
${\cal{X}}=\operatorname{Ul}^s_I(R)$
due to Corollary 4.7.
Note that if
![]() $\cal{X}$
is closed under taking extensions in
$\cal{X}$
is closed under taking extensions in
![]() ${\operatorname{mod}}\ R$
, then
${\operatorname{mod}}\ R$
, then
![]() $({\cal{X}},{\cal{S}}|_{\cal{X}})$
is exact subcategory of
$({\cal{X}},{\cal{S}}|_{\cal{X}})$
is exact subcategory of
![]() ${\operatorname{mod}}\ R$
by Proposition 3.5. In this case,
${\operatorname{mod}}\ R$
by Proposition 3.5. In this case,
![]() ${\operatorname{Ext}}^1_{\cal{X}}(M,N)={\operatorname{Ext}}^1_{R}(M,N)$
for all
${\operatorname{Ext}}^1_{\cal{X}}(M,N)={\operatorname{Ext}}^1_{R}(M,N)$
for all
![]() $M,N\in {\cal{X}}$
.
$M,N\in {\cal{X}}$
.
Definition 4.10. Let
![]() $\cal{X}$
be a subcategory of
$\cal{X}$
be a subcategory of
![]() ${\operatorname{mod}}\ R$
such that
${\operatorname{mod}}\ R$
such that
![]() $({\cal{X}},{\cal{S}}|_{\cal{X}})$
is an exact subcategory of
$({\cal{X}},{\cal{S}}|_{\cal{X}})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
, and let
${\operatorname{mod}}\ R$
, and let
![]() $\phi :{\cal{X}}\to \mathbb Z$
be a function satisfying the hypothesis of Theorem 4.8, that is,
$\phi :{\cal{X}}\to \mathbb Z$
be a function satisfying the hypothesis of Theorem 4.8, that is,
![]() $\phi $
is constant on isomorphism classes of modules in
$\phi $
is constant on isomorphism classes of modules in
![]() $\cal{X}$
,
$\cal{X}$
,
![]() $\phi $
is additive on finite direct sums, and subadditive on short exact sequences of modules in
$\phi $
is additive on finite direct sums, and subadditive on short exact sequences of modules in
![]() $\cal{X}$
. Then, in the notation of Theorem 4.8,
$\cal{X}$
. Then, in the notation of Theorem 4.8,
![]() $({\cal{X}},{\cal{S}}|_{{\cal{X}}^{\phi }})$
is an exact subcategory of
$({\cal{X}},{\cal{S}}|_{{\cal{X}}^{\phi }})$
is an exact subcategory of
![]() $({\cal{X}},{\cal{S}}|_{\cal{X}})$
, hence an exact subcategory of
$({\cal{X}},{\cal{S}}|_{\cal{X}})$
, hence an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. For
${\operatorname{mod}}\ R$
. For
![]() $M,N\in {\cal{X}}$
, define
$M,N\in {\cal{X}}$
, define
![]() ${\operatorname{Ext}}_{\cal{X}}^1(M,N)^{\phi }:={\operatorname{Ext}}_{{\cal{S}}|_{{\cal{X}}^{\phi }}}(M,N)=\{[\alpha ]\in {\operatorname{Ext}}_{\cal{X}}^1(M,N)\text { }:\text { }\phi \text { is additive on }\alpha \}$
. Again, we notice that if
${\operatorname{Ext}}_{\cal{X}}^1(M,N)^{\phi }:={\operatorname{Ext}}_{{\cal{S}}|_{{\cal{X}}^{\phi }}}(M,N)=\{[\alpha ]\in {\operatorname{Ext}}_{\cal{X}}^1(M,N)\text { }:\text { }\phi \text { is additive on }\alpha \}$
. Again, we notice that if
![]() ${\cal{X}}\subseteq {\operatorname{mod}}\ R$
is closed under taking extensions, then
${\cal{X}}\subseteq {\operatorname{mod}}\ R$
is closed under taking extensions, then
![]() ${\operatorname{Ext}}_{\cal{X}}^1(M,N)^{\phi } =\{[\alpha ]\in {\operatorname{Ext}}^1_{R}(M,N)\text { }:\text { }\phi \text { is additive on }\alpha \}$
, and in this case, we denote it just by
${\operatorname{Ext}}_{\cal{X}}^1(M,N)^{\phi } =\{[\alpha ]\in {\operatorname{Ext}}^1_{R}(M,N)\text { }:\text { }\phi \text { is additive on }\alpha \}$
, and in this case, we denote it just by
![]() ${\operatorname{Ext}}^1_R(M,N)^{\phi }$
.
${\operatorname{Ext}}^1_R(M,N)^{\phi }$
.
4.11. Note that
![]() ${\operatorname{Ext}}_{\cal{X}}^1(-,-)^{\phi }:{\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
is a subfunctor of
${\operatorname{Ext}}_{\cal{X}}^1(-,-)^{\phi }:{\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
is a subfunctor of
![]() ${\operatorname{Ext}}_{\cal{X}}^1(-,-):{\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
, which in turn is a subfunctor of
${\operatorname{Ext}}_{\cal{X}}^1(-,-):{\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
, which in turn is a subfunctor of
![]() ${\operatorname{Ext}}^1_{R}(-,-):{\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
(Proposition 3.8) and we have corresponding commutative diagram of long exact sequences by Corollary 3.9.
${\operatorname{Ext}}^1_{R}(-,-):{\cal{X}}^{op}\times {\cal{X}}\to {\operatorname{mod}}\ R$
(Proposition 3.8) and we have corresponding commutative diagram of long exact sequences by Corollary 3.9.
With the extension-closed subcategory
![]() ${\cal{X}}={\operatorname{mod}}\ R$
, where
${\cal{X}}={\operatorname{mod}}\ R$
, where
![]() $(R,\mathfrak {m},k)$
is a Noetherian local ring, and the subadditive function
$(R,\mathfrak {m},k)$
is a Noetherian local ring, and the subadditive function
![]() $\phi (-)=\mu (-):{\operatorname{mod}}\ R\to \mathbb Z$
being the number of generators function in Definition 4.10, we see that
$\phi (-)=\mu (-):{\operatorname{mod}}\ R\to \mathbb Z$
being the number of generators function in Definition 4.10, we see that
![]() ${\operatorname{Ext}}^1_R(M,N)^{\mu }=\langle M, N\rangle $
in the notation of [Reference Striuli35, Def. 1.35]. So, by our discussion, Theorem 4.8, Proposition 3.8, and Corollary 3.9 recover [Reference Striuli35, Cor. 1.36 and Props. 1.37 and 1.38].
${\operatorname{Ext}}^1_R(M,N)^{\mu }=\langle M, N\rangle $
in the notation of [Reference Striuli35, Def. 1.35]. So, by our discussion, Theorem 4.8, Proposition 3.8, and Corollary 3.9 recover [Reference Striuli35, Cor. 1.36 and Props. 1.37 and 1.38].
Before we apply our discussion to more certain special cases, we record one preliminary lemma.
Lemma 4.12. Let
![]() $({\cal{X}},{\cal{E}})$
be an exact subcategory of
$({\cal{X}},{\cal{E}})$
be an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. Let
${\operatorname{mod}}\ R$
. Let
![]() $G:{\cal{X}} \to \operatorname{fl}(R)$
be an additive half-exact functor, where
$G:{\cal{X}} \to \operatorname{fl}(R)$
be an additive half-exact functor, where
![]() $\operatorname{fl}(R)$
denotes the full subcategory of
$\operatorname{fl}(R)$
denotes the full subcategory of
![]() ${\operatorname{mod}}\ R$
consisting of finite length modules. Then,
${\operatorname{mod}}\ R$
consisting of finite length modules. Then,
![]() $\phi (-):=\lambda _R(G(-)): {\cal{X}} \to \mathbb Z$
satisfies the hypothesis of Theorem 4.8. Moreover, given a short exact sequence
$\phi (-):=\lambda _R(G(-)): {\cal{X}} \to \mathbb Z$
satisfies the hypothesis of Theorem 4.8. Moreover, given a short exact sequence
![]() $\sigma $
with objects in
$\sigma $
with objects in
![]() $\cal{X}$
,
$\cal{X}$
,
![]() $G(\sigma )$
is a short exact sequence of modules if and only if
$G(\sigma )$
is a short exact sequence of modules if and only if
![]() $\phi $
is additive on
$\phi $
is additive on
![]() $\sigma $
.
$\sigma $
.
Proof. We will only prove the statement when G is a covariant functor, since the proof for a contravariant functor is similar. Since G is a functor and
![]() $\lambda _R$
is constant on isomorphism classes of objects in
$\lambda _R$
is constant on isomorphism classes of objects in
![]() ${\operatorname{mod}}\ R$
,
${\operatorname{mod}}\ R$
,
![]() $\phi $
is constant on isomorphism classes of objects in
$\phi $
is constant on isomorphism classes of objects in
![]() $\cal{X}$
. Let
$\cal{X}$
. Let
![]() $A,B\in {\cal{X}}$
. Then
$A,B\in {\cal{X}}$
. Then
![]() $\phi (A\oplus B)=\lambda _R(G(A\oplus B))=\lambda _R(G(A)\oplus G(B))=\lambda _R(G(A))+\lambda _R(G(B))=\phi (A)+\phi (B)$
, so
$\phi (A\oplus B)=\lambda _R(G(A\oplus B))=\lambda _R(G(A)\oplus G(B))=\lambda _R(G(A))+\lambda _R(G(B))=\phi (A)+\phi (B)$
, so
![]() $\phi $
is additive on finite biproducts. Next, let
$\phi $
is additive on finite biproducts. Next, let
![]() $\sigma :0\to M\xrightarrow {f} N\xrightarrow {g} L\to 0$
be a short exact sequence with objects in
$\sigma :0\to M\xrightarrow {f} N\xrightarrow {g} L\to 0$
be a short exact sequence with objects in
![]() $\cal{X}$
. Then
$\cal{X}$
. Then
![]() $G(\sigma )$
is the exact sequence
$G(\sigma )$
is the exact sequence
![]() $G(\sigma ):0\to K\to G(M)\xrightarrow {G(f)} G(N)\xrightarrow {G(g)} G(L)\to P\to 0$
, where
$G(\sigma ):0\to K\to G(M)\xrightarrow {G(f)} G(N)\xrightarrow {G(g)} G(L)\to P\to 0$
, where
![]() $K=\operatorname{Ker}(G(f))$
and
$K=\operatorname{Ker}(G(f))$
and
![]() $P=\operatorname{Coker}(G(g))$
. Then we have
$P=\operatorname{Coker}(G(g))$
. Then we have
![]() $\phi (M)+\phi (L)-\phi (N)=\lambda _R(G(M))+\lambda _R(G(L))-\lambda _R(G(N))=\lambda _R(K)+\lambda _R(P)\geq 0$
, so
$\phi (M)+\phi (L)-\phi (N)=\lambda _R(G(M))+\lambda _R(G(L))-\lambda _R(G(N))=\lambda _R(K)+\lambda _R(P)\geq 0$
, so
![]() $\phi (M)+\phi (L)\ge \phi (N)$
. Hence,
$\phi (M)+\phi (L)\ge \phi (N)$
. Hence,
![]() $\phi $
is subadditive on a short exact sequence with objects in
$\phi $
is subadditive on a short exact sequence with objects in
![]() $\cal{X}$
. Thus,
$\cal{X}$
. Thus,
![]() $\phi $
satisfies the hypothesis of Proposition 4.8. Next, let
$\phi $
satisfies the hypothesis of Proposition 4.8. Next, let
![]() $\sigma :0\to M\xrightarrow {f} N\xrightarrow {g} L\to 0$
be a short exact sequence with objects in
$\sigma :0\to M\xrightarrow {f} N\xrightarrow {g} L\to 0$
be a short exact sequence with objects in
![]() $\cal{X}$
. Then
$\cal{X}$
. Then
![]() $G(\sigma )$
is short exact if and only if
$G(\sigma )$
is short exact if and only if
![]() $K=\operatorname{Ker}(G(f))=0$
and
$K=\operatorname{Ker}(G(f))=0$
and
![]() $P=\operatorname{Coker}(G(g))=0$
if and only if
$P=\operatorname{Coker}(G(g))=0$
if and only if
![]() $\lambda _R(K)=\lambda _R(P)=0$
if and only if
$\lambda _R(K)=\lambda _R(P)=0$
if and only if
![]() $\phi (M)+\phi (L)-\phi (N)=\lambda _R(G(M))+\lambda _R(G(L))-\lambda _R(G(N))=\lambda _R(K)+\lambda _R(P)= 0$
if and only if
$\phi (M)+\phi (L)-\phi (N)=\lambda _R(G(M))+\lambda _R(G(L))-\lambda _R(G(N))=\lambda _R(K)+\lambda _R(P)= 0$
if and only if
![]() $\phi (M)+\phi (L)=\phi (N)$
if and only if
$\phi (M)+\phi (L)=\phi (N)$
if and only if
![]() $\phi $
is additive on
$\phi $
is additive on
![]() $\sigma $
.
$\sigma $
.
Corollary 4.13. Let
![]() $({\cal{X}},{\cal{E}})$
be an exact subcategory of
$({\cal{X}},{\cal{E}})$
be an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. Let
${\operatorname{mod}}\ R$
. Let
![]() $G:{\cal{X}} \to \operatorname{fl}(R)$
be an additive half-exact functor, where
$G:{\cal{X}} \to \operatorname{fl}(R)$
be an additive half-exact functor, where
![]() $\operatorname{fl}(R)$
denotes the full subcategory of
$\operatorname{fl}(R)$
denotes the full subcategory of
![]() ${\operatorname{mod}}\ R$
consisting of finite length modules. Set
${\operatorname{mod}}\ R$
consisting of finite length modules. Set
![]() ${\cal{E}}^G:=\{\sigma \in {\cal{E}}: G(\sigma ) \text { is a short exact sequence of modules}\}$
. Then,
${\cal{E}}^G:=\{\sigma \in {\cal{E}}: G(\sigma ) \text { is a short exact sequence of modules}\}$
. Then,
![]() $({\cal{X}}, {\cal{E}}^G)$
is an exact subcategory of
$({\cal{X}}, {\cal{E}}^G)$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
.
${\operatorname{mod}}\ R$
.
Proof. From Lemma 4.12, it follows that
![]() ${\cal{E}}^G={\cal{E}}^{\phi }$
, where
${\cal{E}}^G={\cal{E}}^{\phi }$
, where
![]() $\phi (-):=\lambda _R(G(-)): {\cal{X}} \to \mathbb Z$
. Hence, the claim now follows from Theorem 4.8.
$\phi (-):=\lambda _R(G(-)): {\cal{X}} \to \mathbb Z$
. Hence, the claim now follows from Theorem 4.8.
Now again, let
![]() ${\cal{X}}={\operatorname{mod}}\ R$
, where R is Noetherian. Basic examples of additive half-exact functors
${\cal{X}}={\operatorname{mod}}\ R$
, where R is Noetherian. Basic examples of additive half-exact functors
![]() $G:{\cal{X}} \to \operatorname{fl}(R)$
are
$G:{\cal{X}} \to \operatorname{fl}(R)$
are
![]() $G(-):={\operatorname{Ext}}^i_R(-,X),{\operatorname{Ext}}^i_R(X,-), \operatorname{Tor}^R_i(X,-)$
, where X is a fixed R-module of finite length and
$G(-):={\operatorname{Ext}}^i_R(-,X),{\operatorname{Ext}}^i_R(X,-), \operatorname{Tor}^R_i(X,-)$
, where X is a fixed R-module of finite length and
![]() $i\ge 0$
is an integer.
$i\ge 0$
is an integer.
Given a collection
![]() ${\cal{C}}\subseteq {\operatorname{mod}}\ R$
, in [Reference Auslander and Solberg1], the authors considered the following:
${\cal{C}}\subseteq {\operatorname{mod}}\ R$
, in [Reference Auslander and Solberg1], the authors considered the following:
 $$ \begin{align*} F_{\cal{C}}(C,A)&:=\{\sigma: 0\to A \to B \to C\to 0\text{ } |\text{ }\operatorname{Hom}_R(X,\sigma) \text{ is short exact for all } X \in {\cal{C}}\},\\ F^{\cal{C}}(C,A)&:=\{\sigma: 0\to A \to B \to C\to 0\text{ }|\text{ }\operatorname{Hom}_R(\sigma,X) \text{ is short exact for all } X \in {\cal{C}}\} \end{align*} $$
$$ \begin{align*} F_{\cal{C}}(C,A)&:=\{\sigma: 0\to A \to B \to C\to 0\text{ } |\text{ }\operatorname{Hom}_R(X,\sigma) \text{ is short exact for all } X \in {\cal{C}}\},\\ F^{\cal{C}}(C,A)&:=\{\sigma: 0\to A \to B \to C\to 0\text{ }|\text{ }\operatorname{Hom}_R(\sigma,X) \text{ is short exact for all } X \in {\cal{C}}\} \end{align*} $$
and showed in [Reference Auslander and Solberg1, Prop. 1.7] that these define subfunctors of
![]() ${\operatorname{Ext}}^1_R(-,-):{\operatorname{mod}}\ R^{op}\times {\operatorname{mod}}\ R \to \textbf {Ab}$
. Using Corollary 4.13, we recover this result when
${\operatorname{Ext}}^1_R(-,-):{\operatorname{mod}}\ R^{op}\times {\operatorname{mod}}\ R \to \textbf {Ab}$
. Using Corollary 4.13, we recover this result when
![]() ${\cal{C}}\subseteq \operatorname{fl}(R)$
as follows.
${\cal{C}}\subseteq \operatorname{fl}(R)$
as follows.
Corollary 4.14. Let R be a commutative Noetherian ring. Let
![]() ${\cal{C}}\subseteq \operatorname{fl}(R)$
. Then,
${\cal{C}}\subseteq \operatorname{fl}(R)$
. Then,
![]() $F_{\cal{C}}(-,-)$
and
$F_{\cal{C}}(-,-)$
and
![]() $F^{\cal{C}}(-,-)$
are subfunctors of
$F^{\cal{C}}(-,-)$
are subfunctors of
![]() ${\operatorname{Ext}}^1_R(-,-):{\operatorname{mod}}\ R^{op}\times {\operatorname{mod}}\ R \to {\operatorname{mod}}\ R$
.
${\operatorname{Ext}}^1_R(-,-):{\operatorname{mod}}\ R^{op}\times {\operatorname{mod}}\ R \to {\operatorname{mod}}\ R$
.
Proof. We only prove the case of
![]() $F_{\cal{C}}(-,-)$
, since the proof of
$F_{\cal{C}}(-,-)$
, since the proof of
![]() $F^{\cal{C}}(-,-)$
is similar.
$F^{\cal{C}}(-,-)$
is similar.
Let
![]() ${\cal{S}}^{\cal{C}}$
be the collection of all short exact sequences
${\cal{S}}^{\cal{C}}$
be the collection of all short exact sequences
![]() $\sigma $
of finitely generated R-modules such that
$\sigma $
of finitely generated R-modules such that
![]() $\operatorname{Hom}_R(X,\sigma )$
is short exact for all
$\operatorname{Hom}_R(X,\sigma )$
is short exact for all
![]() $X \in {\cal{C}}$
. We first prove that
$X \in {\cal{C}}$
. We first prove that
![]() $({\operatorname{mod}}\ R,{\cal{S}}^{\cal{C}})$
is an exact subcategory of
$({\operatorname{mod}}\ R,{\cal{S}}^{\cal{C}})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. Since
${\operatorname{mod}}\ R$
. Since
![]() ${\cal{S}}^{\cal{C}}=\cap _{C \in {\cal{C}}} {\cal{S}}^{C}$
, it is enough to prove that for each
${\cal{S}}^{\cal{C}}=\cap _{C \in {\cal{C}}} {\cal{S}}^{C}$
, it is enough to prove that for each
![]() $C\in {\cal{C}}$
,
$C\in {\cal{C}}$
,
![]() ${\cal{S}}^C$
gives an exact substructure on
${\cal{S}}^C$
gives an exact substructure on
![]() ${\operatorname{mod}}\ R$
(intersection of exact substructures is again an exact substructure by Lemma 3.2). Now, note that
${\operatorname{mod}}\ R$
(intersection of exact substructures is again an exact substructure by Lemma 3.2). Now, note that
![]() ${\cal{S}}^C=\{\sigma : G(\sigma ) \text { is short exact}\}$
, where
${\cal{S}}^C=\{\sigma : G(\sigma ) \text { is short exact}\}$
, where
![]() $G:{\operatorname{mod}}\ R \to \operatorname{fl}(R)$
is given by
$G:{\operatorname{mod}}\ R \to \operatorname{fl}(R)$
is given by
![]() $G(-):=\operatorname{Hom}_R(C,-)$
, so by Corollary 4.13 we get that
$G(-):=\operatorname{Hom}_R(C,-)$
, so by Corollary 4.13 we get that
![]() $({\operatorname{mod}}\ R,{\cal{S}}^C)$
is an exact subcategory of
$({\operatorname{mod}}\ R,{\cal{S}}^C)$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. Since
${\operatorname{mod}}\ R$
. Since
![]() ${\operatorname{Ext}}_{{\cal{S}}^{\cal{C}}}(-,-)=F_{\cal{C}}(-,-)$
, by Proposition 3.8 we are done.
${\operatorname{Ext}}_{{\cal{S}}^{\cal{C}}}(-,-)=F_{\cal{C}}(-,-)$
, by Proposition 3.8 we are done.
Next, we recover and improve upon [Reference Puthenpurakal31, Ths. 3.11 and 3.13].
For a Noetherian local ring
![]() $(R,\mathfrak {m})$
, let
$(R,\mathfrak {m})$
, let
![]() $\operatorname{MD}(R)$
denote the full subcategory of
$\operatorname{MD}(R)$
denote the full subcategory of
![]() ${\operatorname{mod}}\ R$
consisting of all modules M such that either
${\operatorname{mod}}\ R$
consisting of all modules M such that either
![]() $M=0$
or
$M=0$
or
![]() $\dim M=\dim R$
. We recall that if I is an
$\dim M=\dim R$
. We recall that if I is an
![]() $\mathfrak {m}$
-primary ideal, then
$\mathfrak {m}$
-primary ideal, then
![]() $e_R(I,-)$
is additive on
$e_R(I,-)$
is additive on
![]() $\operatorname{MD}(R)$
. We also recall that a finitely generated module M satisfies Serre’s condition
$\operatorname{MD}(R)$
. We also recall that a finitely generated module M satisfies Serre’s condition
![]() $(S_n)$
if
$(S_n)$
if
![]() $\operatorname{depth}\ M_{\mathfrak {p}}\ge \inf \{n,\dim R_{\mathfrak {p}}\}$
for all
$\operatorname{depth}\ M_{\mathfrak {p}}\ge \inf \{n,\dim R_{\mathfrak {p}}\}$
for all
![]() $\mathfrak {p}\in \operatorname{Spec} R$
. The full subcategory of
$\mathfrak {p}\in \operatorname{Spec} R$
. The full subcategory of
![]() ${\operatorname{mod}}\ R$
consisting of all modules satisfying
${\operatorname{mod}}\ R$
consisting of all modules satisfying
![]() $(S_n)$
is denoted by
$(S_n)$
is denoted by
![]() $S_n(R)$
. Note that
$S_n(R)$
. Note that
![]() $S_n(R)$
is closed under extensions in
$S_n(R)$
is closed under extensions in
![]() ${\operatorname{mod}}\ R$
.
${\operatorname{mod}}\ R$
.
Lemma 4.15. Let R be an equidimensional local ring. Let
![]() $S_1(R)$
be the collection of all modules in
$S_1(R)$
be the collection of all modules in
![]() ${\operatorname{mod}}\ R$
satisfying Serre’s condition
${\operatorname{mod}}\ R$
satisfying Serre’s condition
![]() $(S_1)$
. Then,
$(S_1)$
. Then,
![]() $S_1(R)\subseteq \operatorname{MD}(R)$
.
$S_1(R)\subseteq \operatorname{MD}(R)$
.
Proof. The hypothesis on R implies that
![]() $\dim (R/\mathfrak {p})=\dim R$
for all
$\dim (R/\mathfrak {p})=\dim R$
for all
![]() $\mathfrak {p} \in \operatorname{Min}(R)$
. So, if
$\mathfrak {p} \in \operatorname{Min}(R)$
. So, if
![]() $0\ne M$
satisfy
$0\ne M$
satisfy
![]() $(S_1)$
, then there exists
$(S_1)$
, then there exists
![]() $\mathfrak {p} \in \operatorname{Ass}(M)\subseteq \operatorname{Min}(R)$
. Hence,
$\mathfrak {p} \in \operatorname{Ass}(M)\subseteq \operatorname{Min}(R)$
. Hence,
![]() $\dim (M)\ge \dim (R/\mathfrak {p})=\dim R$
, and we are done.
$\dim (M)\ge \dim (R/\mathfrak {p})=\dim R$
, and we are done.
Now, inspecting the proof of [Reference Puthenpurakal30, Prop. 17], the only place, where R is Cohen–Macaulay and M is maximal Cohen–Macaulay are required, is to ensure that
![]() $e_R(I,-)$
is additive on
$e_R(I,-)$
is additive on
![]() $0\to \Omega _R M \to F \to M \to 0$
and that
$0\to \Omega _R M \to F \to M \to 0$
and that
![]() $M,\Omega _R M \in \operatorname{MD}(R)$
. But if we assume R is equidimensional and satisfy
$M,\Omega _R M \in \operatorname{MD}(R)$
. But if we assume R is equidimensional and satisfy
![]() $(S_1)$
, and
$(S_1)$
, and
![]() $M\in S_1(R)\subseteq \operatorname{MD}(R)$
, then since
$M\in S_1(R)\subseteq \operatorname{MD}(R)$
, then since
![]() $\Omega _R M\in S_1(R)\subseteq \operatorname{MD}(R)$
(Lemma 4.15) and
$\Omega _R M\in S_1(R)\subseteq \operatorname{MD}(R)$
(Lemma 4.15) and
![]() $e_R(I,-)$
is additive on short exact sequence of modules of the same dimension [Reference Bruns and Herzog3, Cor. 4.7.7]; hence, we get the following lemma by following the same proof as in [Reference Puthenpurakal30, Prop. 17].
$e_R(I,-)$
is additive on short exact sequence of modules of the same dimension [Reference Bruns and Herzog3, Cor. 4.7.7]; hence, we get the following lemma by following the same proof as in [Reference Puthenpurakal30, Prop. 17].
Lemma 4.16. Let
![]() $(R,\mathfrak {m})$
be an equidimensional local ring satisfying
$(R,\mathfrak {m})$
be an equidimensional local ring satisfying
![]() $(S_1)$
. Let
$(S_1)$
. Let
![]() $M\in S_1(R)$
. Let
$M\in S_1(R)$
. Let
![]() $d=\dim R\ge 1$
, and let I be an
$d=\dim R\ge 1$
, and let I be an
![]() $\mathfrak {m}$
-primary ideal. Then, the function
$\mathfrak {m}$
-primary ideal. Then, the function
![]() $n \mapsto \lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))$
is given by a polynomial of degree
$n \mapsto \lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))$
is given by a polynomial of degree
![]() $\le d-1$
for
$\le d-1$
for
![]() $n\gg 0$
. So, in particular, the limit
$n\gg 0$
. So, in particular, the limit
 $\lim _{n\to \infty }\dfrac {\lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))}{n^{d-1}}$
exists.
$\lim _{n\to \infty }\dfrac {\lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))}{n^{d-1}}$
exists.
If R and M are as in Lemma 4.16, then let us denote
 $e^T_I(M):=(d-1)!\lim _{n\to \infty }\dfrac {\lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))}{n^{d-1}}$
. (What [Reference Puthenpurakal31] denotes by
$e^T_I(M):=(d-1)!\lim _{n\to \infty }\dfrac {\lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))}{n^{d-1}}$
. (What [Reference Puthenpurakal31] denotes by
![]() $e^T_R(M)$
is exactly the same as
$e^T_R(M)$
is exactly the same as
![]() $e^T_{\mathfrak {m}}(M)$
in our notation.)
$e^T_{\mathfrak {m}}(M)$
in our notation.)
The following theorem generalizes [Reference Puthenpurakal31, Ths. 3.11 and 3.13] owing to the fact that a local Cohen–Macaulay ring R is equidimensional, satisfies
![]() $(S_1)$
and
$(S_1)$
and
![]() $\operatorname{CM}(R)\subseteq S_1(R)$
.
$\operatorname{CM}(R)\subseteq S_1(R)$
.
Theorem 4.17. Let
![]() $(R,\mathfrak {m})$
be an equidimensional local ring satisfying
$(R,\mathfrak {m})$
be an equidimensional local ring satisfying
![]() $(S_1)$
. Let
$(S_1)$
. Let
![]() ${\cal{X}}=S_1(R)$
be the subcategory of
${\cal{X}}=S_1(R)$
be the subcategory of
![]() ${\operatorname{mod}}\ R$
consisting of all modules satisfying
${\operatorname{mod}}\ R$
consisting of all modules satisfying
![]() $(S_1)$
. Let I be an
$(S_1)$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal. Then,
$\mathfrak {m}$
-primary ideal. Then,
![]() ${\operatorname{Ext}}^1_R(-,-)^{e_I^T}:S_1(R)^{op}\times S_1(R)\to {\operatorname{mod}}\ R$
is a subfunctor of
${\operatorname{Ext}}^1_R(-,-)^{e_I^T}:S_1(R)^{op}\times S_1(R)\to {\operatorname{mod}}\ R$
is a subfunctor of
![]() ${\operatorname{Ext}}^1_R(-,-):S_1(R)^{op}\times S_1(R)\to {\operatorname{mod}}\ R$
.
${\operatorname{Ext}}^1_R(-,-):S_1(R)^{op}\times S_1(R)\to {\operatorname{mod}}\ R$
.
Proof. Since
![]() $S_1(R)$
is an extension closed subcategory of
$S_1(R)$
is an extension closed subcategory of
![]() ${\operatorname{mod}}\ R$
, we have
${\operatorname{mod}}\ R$
, we have
![]() $(S_1(R),{\cal{S}}|_{S_1(R)})$
is an exact subcategory of
$(S_1(R),{\cal{S}}|_{S_1(R)})$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. Since for each n, the function
${\operatorname{mod}}\ R$
. Since for each n, the function
![]() ${\operatorname{mod}}\ R \to \mathbb Z$
given by
${\operatorname{mod}}\ R \to \mathbb Z$
given by
![]() $M\mapsto \lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))$
is subadditive on short exact sequences of
$M\mapsto \lambda (\operatorname{Tor}^R_1(M,R/I^{n+1}))$
is subadditive on short exact sequences of
![]() ${\operatorname{mod}}\ R$
, we have
${\operatorname{mod}}\ R$
, we have
![]() $e^T_I:S_1(R)\to \mathbb Z$
is also subadditive on short exact sequences of
$e^T_I:S_1(R)\to \mathbb Z$
is also subadditive on short exact sequences of
![]() $S_1(R)$
. Thus,
$S_1(R)$
. Thus,
![]() $(S_1(R),{\cal{S}}|_{S_1(R)}^{e^T_I})$
is an exact subcategory of
$(S_1(R),{\cal{S}}|_{S_1(R)}^{e^T_I})$
is an exact subcategory of
![]() $(S_1(R),{\cal{S}}|_{S_1(R)})$
by Theorem 4.8. Hence, we are done by Proposition 3.8.
$(S_1(R),{\cal{S}}|_{S_1(R)})$
by Theorem 4.8. Hence, we are done by Proposition 3.8.
5 Special subfunctors of
 ${\operatorname{Ext}}^1$
and applications
${\operatorname{Ext}}^1$
and applications
Throughout this section, R will denote a Noetherian local ring with unique maximal ideal
![]() $\mathfrak {m}$
and residue field k. We will denote by
$\mathfrak {m}$
and residue field k. We will denote by
![]() $\mu _R(-)$
the minimal number of generators function for finitely generated modules, that is,
$\mu _R(-)$
the minimal number of generators function for finitely generated modules, that is,
![]() $\mu _R(M)=\lambda _R(M\otimes _R R/\mathfrak {m})$
for all
$\mu _R(M)=\lambda _R(M\otimes _R R/\mathfrak {m})$
for all
![]() $M\in {\operatorname{mod}}\ R$
. We drop the subscript R when the ring in question is clear. We shall study properties and applications of a number of subfunctors of
$M\in {\operatorname{mod}}\ R$
. We drop the subscript R when the ring in question is clear. We shall study properties and applications of a number of subfunctors of
![]() ${\operatorname{Ext}}^1$
, whose existence follow from results in previous sections.
${\operatorname{Ext}}^1$
, whose existence follow from results in previous sections.
5.1 Some computations and applications of the subfunctor
 ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
We start this subsection with a characterization of regularity among Cohen–Macaulay rings of positive dimension d in terms of vanishing of certain
![]() ${\operatorname{Ext}}^1_R(-,-)^{\mu }$
(see Definition 4.10 and the discussion after 4.11 for notation).
${\operatorname{Ext}}^1_R(-,-)^{\mu }$
(see Definition 4.10 and the discussion after 4.11 for notation).
Theorem 5.1.1. Let R be a local Cohen–Macaulay ring of dimension
![]() $d\ge 1$
. Then, R is regular if and only if
$d\ge 1$
. Then, R is regular if and only if
![]() ${\operatorname{Ext}}^1_R(\Omega ^{d-1}_R k, N)^{\mu }=0$
for some finitely generated nonzero R-module N of finite injective dimension.
${\operatorname{Ext}}^1_R(\Omega ^{d-1}_R k, N)^{\mu }=0$
for some finitely generated nonzero R-module N of finite injective dimension.
When R is regular, we show
![]() ${\operatorname{Ext}}^1_R(\Omega ^{d-1}_R k, R)^{\mu }=0$
, which shows one direction of Theorem 5.1.1. For this, we first need two preliminary lemmas.
${\operatorname{Ext}}^1_R(\Omega ^{d-1}_R k, R)^{\mu }=0$
, which shows one direction of Theorem 5.1.1. For this, we first need two preliminary lemmas.
Lemma 5.1.2. Let Y be a submodule of an R-module X such that
![]() $\mathfrak {m} X\subseteq Y$
. If X is cyclic and
$\mathfrak {m} X\subseteq Y$
. If X is cyclic and
![]() $Y\ne X$
, then
$Y\ne X$
, then
![]() $Y=\mathfrak {m} X$
.
$Y=\mathfrak {m} X$
.
Proof. We prove that if
![]() $Y\ne \mathfrak {m} X$
, then
$Y\ne \mathfrak {m} X$
, then
![]() $Y=X$
. If
$Y=X$
. If
![]() $Y\ne \mathfrak {m} X$
, then pick
$Y\ne \mathfrak {m} X$
, then pick
![]() $y\in Y\setminus \mathfrak {m} X\subseteq X\setminus \mathfrak {m} X$
. Then, y is part of a minimal system of generators of X, but X is cyclic, so
$y\in Y\setminus \mathfrak {m} X\subseteq X\setminus \mathfrak {m} X$
. Then, y is part of a minimal system of generators of X, but X is cyclic, so
![]() $X=Ry$
. Also,
$X=Ry$
. Also,
![]() $Ry\subseteq Y\subseteq X$
. Hence,
$Ry\subseteq Y\subseteq X$
. Hence,
![]() $Y=X$
.
$Y=X$
.
Lemma 5.1.3. Let M be a finitely generated R-module with the first Betti number
![]() $1$
. Then,
$1$
. Then,
![]() ${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(M,\Omega _R M)$
.
${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(M,\Omega _R M)$
.
Proof.
![]() ${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }$
is a submodule of
${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }$
is a submodule of
![]() ${\operatorname{Ext}}^1_R(M,\Omega _R M)$
such that
${\operatorname{Ext}}^1_R(M,\Omega _R M)$
such that
![]() $\mathfrak {m} {\operatorname{Ext}}^1_R(M,\Omega _R M)\subseteq {\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }$
by Lemma 5.2.1. By hypothesis, we have
$\mathfrak {m} {\operatorname{Ext}}^1_R(M,\Omega _R M)\subseteq {\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }$
by Lemma 5.2.1. By hypothesis, we have
![]() $\Omega _R M\cong R/I$
for some ideal
$\Omega _R M\cong R/I$
for some ideal
![]() $I\ne R$
, and we have an exact sequence
$I\ne R$
, and we have an exact sequence
![]() $ 0\to R/I \to F \to M \to 0$
, for some free R-module F. So, in particular,
$ 0\to R/I \to F \to M \to 0$
, for some free R-module F. So, in particular,
![]() $\mu (F)=\mu (M)\ne \mu (R/I)+\mu (M)$
. Hence, this exact sequence is not
$\mu (F)=\mu (M)\ne \mu (R/I)+\mu (M)$
. Hence, this exact sequence is not
![]() $\mu $
-additive. So,
$\mu $
-additive. So,
![]() ${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }\ne {\operatorname{Ext}}^1_R(M,\Omega _R M)$
. Also, applying
${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }\ne {\operatorname{Ext}}^1_R(M,\Omega _R M)$
. Also, applying
![]() $\operatorname{Hom}_R(-,R/I)$
to the exact sequence
$\operatorname{Hom}_R(-,R/I)$
to the exact sequence
![]() $0\to R/I \to F \to M \to 0$
, we get an exact sequence
$0\to R/I \to F \to M \to 0$
, we get an exact sequence
 $0\to \operatorname{Hom}_R(M,R/I)\to \operatorname{Hom}_R(F,R/I)\to \operatorname{Hom}_R(R/I,R/I)\cong R/I \to {\operatorname{Ext}}^1_R(M,R/I)\cong {\operatorname{Ext}}^1_R(M,\Omega _RM)\to 0$
. Hence,
$0\to \operatorname{Hom}_R(M,R/I)\to \operatorname{Hom}_R(F,R/I)\to \operatorname{Hom}_R(R/I,R/I)\cong R/I \to {\operatorname{Ext}}^1_R(M,R/I)\cong {\operatorname{Ext}}^1_R(M,\Omega _RM)\to 0$
. Hence,
![]() ${\operatorname{Ext}}^1_R(M,\Omega _R M)$
is a cyclic module. Now, applying Lemma 5.1.2 to
${\operatorname{Ext}}^1_R(M,\Omega _R M)$
is a cyclic module. Now, applying Lemma 5.1.2 to
![]() $Y={\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }$
and
$Y={\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }$
and
![]() $X={\operatorname{Ext}}^1_R(M,\Omega _R M)$
, we get
$X={\operatorname{Ext}}^1_R(M,\Omega _R M)$
, we get
![]() ${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(M,\Omega _R M)$
.
${\operatorname{Ext}}^1_R(M,\Omega _R M)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(M,\Omega _R M)$
.
Now, one direction of Theorem 5.1.1 is the following.
Corollary 5.1.4. Let
![]() $(R,\mathfrak {m},k)$
be a regular local ring of dimension
$(R,\mathfrak {m},k)$
be a regular local ring of dimension
![]() $d\ge 1$
. Then,
$d\ge 1$
. Then,
![]() ${\operatorname{Ext}}^1_R(\Omega ^{d-1}_R k, R)^{\mu }=0$
.
${\operatorname{Ext}}^1_R(\Omega ^{d-1}_R k, R)^{\mu }=0$
.
Proof. We know
![]() $\Omega _R \Omega ^{d-1}_R k\cong R$
by looking at the Koszul complex of
$\Omega _R \Omega ^{d-1}_R k\cong R$
by looking at the Koszul complex of
![]() $R/\mathfrak {m}$
, so the first Betti number of
$R/\mathfrak {m}$
, so the first Betti number of
![]() $\Omega ^{d-1}_R k$
is
$\Omega ^{d-1}_R k$
is
![]() $1$
. Hence, by Lemma 5.1.3, we get that
$1$
. Hence, by Lemma 5.1.3, we get that
![]() ${\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,R)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,R)\cong \mathfrak {m}{\operatorname{Ext}}^d_R(k,R)\cong \mathfrak {m}\cdot k=0$
.
${\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,R)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,R)\cong \mathfrak {m}{\operatorname{Ext}}^d_R(k,R)\cong \mathfrak {m}\cdot k=0$
.
The other direction of Theorem 5.1.1 requires more work. First, we begin with the following setup.
5.1.5. Let
![]() $(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of dimension
![]() $d\ge 1$
admitting a canonical module
$d\ge 1$
admitting a canonical module
![]() $\omega _R$
. Then,
$\omega _R$
. Then,
![]() ${\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,\omega _R)\cong k$
. Hence, for any two non-split exact sequences
${\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,\omega _R)\cong k$
. Hence, for any two non-split exact sequences
![]() $\alpha , \beta \in {\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,\omega _R)$
, we have
$\alpha , \beta \in {\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,\omega _R)$
, we have
![]() $[\beta ]=r[\alpha ] \in {\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,\omega _R)$
for some unit
$[\beta ]=r[\alpha ] \in {\operatorname{Ext}}^1_R(\Omega ^{d-1}_Rk,\omega _R)$
for some unit
![]() $r\in R$
. So, we have the following pushout diagram:
$r\in R$
. So, we have the following pushout diagram:

Since
![]() $r\in R$
is a unit, we have
$r\in R$
is a unit, we have
![]() $\omega _R \xrightarrow {\cdot r} \omega _R$
is an isomorphism. Hence, by five lemma,
$\omega _R \xrightarrow {\cdot r} \omega _R$
is an isomorphism. Hence, by five lemma,
![]() $X_{\alpha }\cong X_{\beta }$
. So, there exists a unique module (up to isomorphism), call it
$X_{\alpha }\cong X_{\beta }$
. So, there exists a unique module (up to isomorphism), call it
![]() $E^R$
, such that the middle term of every non-split exact sequence
$E^R$
, such that the middle term of every non-split exact sequence
![]() $0\to \omega _R \to X \to \Omega ^{d-1} k \to 0$
is isomorphic to
$0\to \omega _R \to X \to \Omega ^{d-1} k \to 0$
is isomorphic to
![]() $E^R$
. Since
$E^R$
. Since
![]() $\Omega ^{d-1}_R k$
has co-depth
$\Omega ^{d-1}_R k$
has co-depth
![]() $1$
, by [Reference Leuschke and Wiegand27, Prop. 11.21], we get that
$1$
, by [Reference Leuschke and Wiegand27, Prop. 11.21], we get that
![]() $0\to \omega _R \to E^R \to \Omega ^{d-1}_Rk \to 0$
is the minimal maximal Cohen--Macaulay (MCM) approximation of
$0\to \omega _R \to E^R \to \Omega ^{d-1}_Rk \to 0$
is the minimal maximal Cohen--Macaulay (MCM) approximation of
![]() $\Omega ^{d-1}_R k$
.
$\Omega ^{d-1}_R k$
.
Moving forward, we denote
![]() $\operatorname{Hom}_R(-,\omega _R)$
by
$\operatorname{Hom}_R(-,\omega _R)$
by
![]() $(-)^{\dagger }$
.
$(-)^{\dagger }$
.
We need to collect some properties of
![]() $E^R$
to prove the other direction of Theorem 5.1.1.
$E^R$
to prove the other direction of Theorem 5.1.1.
Lemma 5.1.6. Let
![]() $(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of dimension
![]() $1$
admitting a canonical module
$1$
admitting a canonical module
![]() $\omega _R$
. Then,
$\omega _R$
. Then,
![]() $E^R\cong \mathfrak {m}^{\dagger }$
.
$E^R\cong \mathfrak {m}^{\dagger }$
.
Proof. Dualizing
![]() $0\to \mathfrak {m} \to R \to k \to 0$
by
$0\to \mathfrak {m} \to R \to k \to 0$
by
![]() $\omega _R$
, we get
$\omega _R$
, we get
![]() $0\to \omega _R \to \mathfrak {m}^{\dagger } \to {\operatorname{Ext}}^1_R(k,\omega _R)\cong k \to 0$
. So, we have the exact sequence
$0\to \omega _R \to \mathfrak {m}^{\dagger } \to {\operatorname{Ext}}^1_R(k,\omega _R)\cong k \to 0$
. So, we have the exact sequence
![]() $0\to \omega _R \to \mathfrak {m}^{\dagger } \to k \to 0$
, which is clearly non-split, since
$0\to \omega _R \to \mathfrak {m}^{\dagger } \to k \to 0$
, which is clearly non-split, since
![]() $\mathfrak {m}^{\dagger }$
has positive depth. But
$\mathfrak {m}^{\dagger }$
has positive depth. But
![]() $k\oplus \omega _R$
has depth
$k\oplus \omega _R$
has depth
![]() $0$
. Thus,
$0$
. Thus,
![]() $E^R\cong \mathfrak {m}^{\dagger }$
.
$E^R\cong \mathfrak {m}^{\dagger }$
.
We record the following lemma, which will be used to deduce further properties of the module
![]() $E^R$
.
$E^R$
.
Lemma 5.1.7. Let
![]() $(R,\mathfrak {m},k)$
be a local ring, and let I be an ideal of R, which is not principal. Then, for every
$(R,\mathfrak {m},k)$
be a local ring, and let I be an ideal of R, which is not principal. Then, for every
![]() $x\in I\setminus \mathfrak {m} I$
, we have
$x\in I\setminus \mathfrak {m} I$
, we have
![]() $(x\mathfrak {m}:_{\mathfrak {m}} I)=(x\mathfrak {m}:_R I)=((x) :_R I)$
.
$(x\mathfrak {m}:_{\mathfrak {m}} I)=(x\mathfrak {m}:_R I)=((x) :_R I)$
.
Proof. Since trivially
![]() $(x\mathfrak {m}:_{\mathfrak {m}}I)\subseteq (x\mathfrak {m}:_R I)\subseteq ((x) :_R I)$
always holds, it is enough to prove the inclusion
$(x\mathfrak {m}:_{\mathfrak {m}}I)\subseteq (x\mathfrak {m}:_R I)\subseteq ((x) :_R I)$
always holds, it is enough to prove the inclusion
![]() $((x) :_R I)\subseteq (x\mathfrak {m}:_{\mathfrak {m}} I)$
. So, let
$((x) :_R I)\subseteq (x\mathfrak {m}:_{\mathfrak {m}} I)$
. So, let
![]() $y\in ((x) :_R I)$
, which means
$y\in ((x) :_R I)$
, which means
![]() $yI \subseteq (x)$
. If y were a unit, then we would have
$yI \subseteq (x)$
. If y were a unit, then we would have
![]() $I \subseteq y^{-1}(x)=(x)\subseteq I$
, implying
$I \subseteq y^{-1}(x)=(x)\subseteq I$
, implying
![]() $I=(x)$
, contradicting our assumption that I is not principal. Thus, we must have
$I=(x)$
, contradicting our assumption that I is not principal. Thus, we must have
![]() $y\in \mathfrak {m}$
. Now, pick an arbitrary element
$y\in \mathfrak {m}$
. Now, pick an arbitrary element
![]() $r\in I$
. Then
$r\in I$
. Then
![]() $yr\in y I\subseteq (x)$
, so
$yr\in y I\subseteq (x)$
, so
![]() $yr=xs$
for some
$yr=xs$
for some
![]() $s\in R$
. If
$s\in R$
. If
![]() $s\notin \mathfrak {m}$
, then
$s\notin \mathfrak {m}$
, then
![]() $x=s^{-1}yr\in \mathfrak {m} I$
, which is a contradiction. Hence,
$x=s^{-1}yr\in \mathfrak {m} I$
, which is a contradiction. Hence,
![]() $s\in \mathfrak {m}$
. So,
$s\in \mathfrak {m}$
. So,
![]() $yr=xs\in x\mathfrak {m}$
. Since
$yr=xs\in x\mathfrak {m}$
. Since
![]() $r\in I$
was arbitrary, we get
$r\in I$
was arbitrary, we get
![]() $yI \subseteq x\mathfrak {m}$
. Hence,
$yI \subseteq x\mathfrak {m}$
. Hence,
![]() $y\in (x\mathfrak {m}:_{\mathfrak {m}} I)$
.
$y\in (x\mathfrak {m}:_{\mathfrak {m}} I)$
.
In the following,
![]() ${\operatorname{r}}(-)$
will denote the type of a module, that is,
${\operatorname{r}}(-)$
will denote the type of a module, that is,
![]() ${\operatorname{r}}(M)= \dim _k {{\operatorname{Ext}}}^{\operatorname{depth}_R M}_R(k,M)$
.
${\operatorname{r}}(M)= \dim _k {{\operatorname{Ext}}}^{\operatorname{depth}_R M}_R(k,M)$
.
Lemma 5.1.8. Let
![]() $(R,\mathfrak {m},k)$
be a non-regular complete local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m},k)$
be a non-regular complete local Cohen–Macaulay ring of dimension
![]() $d\ge 1$
, with canonical module
$d\ge 1$
, with canonical module
![]() $\omega _R$
. Then, we have
$\omega _R$
. Then, we have
![]() $\mu (E^R)=\operatorname{r}(R)+\mu (\Omega ^{d-1}_Rk)$
.
$\mu (E^R)=\operatorname{r}(R)+\mu (\Omega ^{d-1}_Rk)$
.
Proof. We prove this by induction on d. First, let
![]() $d=1$
. By Lemma 5.1.6, we have
$d=1$
. By Lemma 5.1.6, we have
![]() $E^R\cong \mathfrak {m}^{\dagger }$
. Pick
$E^R\cong \mathfrak {m}^{\dagger }$
. Pick
![]() $x\in \mathfrak {m}\setminus \mathfrak {m}^2$
to be R-regular. Then
$x\in \mathfrak {m}\setminus \mathfrak {m}^2$
to be R-regular. Then
![]() $\mu _R(E^R)=\mu _{R/xR}(E^R/xE^R)$
. Now,
$\mu _R(E^R)=\mu _{R/xR}(E^R/xE^R)$
. Now,
![]() $E^R/x E^R\cong \mathfrak {m}^{\dagger }/x\mathfrak {m}^{\dagger }\cong \operatorname{Hom}_{R/xR}(\mathfrak {m}/x\mathfrak {m},\omega _R/x\omega _R)\cong (\mathfrak {m}/x\mathfrak {m})^{\dagger }$
(where the last two isomorphisms follow from [Reference Bruns and Herzog3, Prop. 3.3.3(a) and Th. 3.3.5(a)]). Now,
$E^R/x E^R\cong \mathfrak {m}^{\dagger }/x\mathfrak {m}^{\dagger }\cong \operatorname{Hom}_{R/xR}(\mathfrak {m}/x\mathfrak {m},\omega _R/x\omega _R)\cong (\mathfrak {m}/x\mathfrak {m})^{\dagger }$
(where the last two isomorphisms follow from [Reference Bruns and Herzog3, Prop. 3.3.3(a) and Th. 3.3.5(a)]). Now,
 $ \operatorname{Hom}_{R/xR}((\mathfrak {m}/x\mathfrak {m})^{\dagger },k)\cong \operatorname{Hom}_{R/xR}(k^{\dagger }, \mathfrak {m}/x\mathfrak {m})\cong \operatorname{Hom}_{R/xR}(k, \mathfrak {m}/x\mathfrak {m})\cong (x\mathfrak {m}:_{\mathfrak {m}}\mathfrak {m})/x\mathfrak {m}=((x):_R\mathfrak {m})/x\mathfrak {m}$
(where the first isomorphism holds because
$ \operatorname{Hom}_{R/xR}((\mathfrak {m}/x\mathfrak {m})^{\dagger },k)\cong \operatorname{Hom}_{R/xR}(k^{\dagger }, \mathfrak {m}/x\mathfrak {m})\cong \operatorname{Hom}_{R/xR}(k, \mathfrak {m}/x\mathfrak {m})\cong (x\mathfrak {m}:_{\mathfrak {m}}\mathfrak {m})/x\mathfrak {m}=((x):_R\mathfrak {m})/x\mathfrak {m}$
(where the first isomorphism holds because
![]() $R/xR$
is Artinian, so one can invoke [Reference Dao and Huneke10, Lem. 3.14 and Rem. 3.15], and the last equality follows from Lemma 5.1.7 since R is not regular). Hence,
$R/xR$
is Artinian, so one can invoke [Reference Dao and Huneke10, Lem. 3.14 and Rem. 3.15], and the last equality follows from Lemma 5.1.7 since R is not regular). Hence,
 $\mu _R(E^R)=\mu _{R/xR}(E^R/xE^R)=\dim _k \operatorname{Hom}_{R/xR}((\mathfrak {m}/x\mathfrak {m})^{\dagger },k)=\dim _k ((x):_R\mathfrak {m})/x\mathfrak {m}=\dim _k \left ((xR:_R \mathfrak {m})/xR \right )+ \dim _k (xR/x\mathfrak {m})=\dim _k \operatorname{Soc}(R/xR)+\dim _k (xR/x\mathfrak {m})=\text {r}(R)+\dim _k (xR/x\mathfrak {m})$
(since
$\mu _R(E^R)=\mu _{R/xR}(E^R/xE^R)=\dim _k \operatorname{Hom}_{R/xR}((\mathfrak {m}/x\mathfrak {m})^{\dagger },k)=\dim _k ((x):_R\mathfrak {m})/x\mathfrak {m}=\dim _k \left ((xR:_R \mathfrak {m})/xR \right )+ \dim _k (xR/x\mathfrak {m})=\dim _k \operatorname{Soc}(R/xR)+\dim _k (xR/x\mathfrak {m})=\text {r}(R)+\dim _k (xR/x\mathfrak {m})$
(since
![]() $xR/x\mathfrak {m}$
is annihilated by
$xR/x\mathfrak {m}$
is annihilated by
![]() $\mathfrak {m}$
, hence it is a k-vector space). Since
$\mathfrak {m}$
, hence it is a k-vector space). Since
![]() $xR/x\mathfrak {m}$
is generated by x and it is a k-vector space, we have
$xR/x\mathfrak {m}$
is generated by x and it is a k-vector space, we have
![]() $xR/x\mathfrak {m}\cong k$
. Hence,
$xR/x\mathfrak {m}\cong k$
. Hence,
![]() $\dim _k (xR/x\mathfrak {m})=1$
, so
$\dim _k (xR/x\mathfrak {m})=1$
, so
![]() $\mu (E^R)=\text {r}(R)+1=\text {r}(R)+\mu (k)$
. This concludes the
$\mu (E^R)=\text {r}(R)+1=\text {r}(R)+\mu (k)$
. This concludes the
![]() $d=1$
case.
$d=1$
case.
Now, let
![]() $\dim R=d>1$
and suppose the claim has been proved for all non-regular local Cohen–Macaulay rings of dimension
$\dim R=d>1$
and suppose the claim has been proved for all non-regular local Cohen–Macaulay rings of dimension
![]() $1,...,d-1$
admitting a canonical module. Since
$1,...,d-1$
admitting a canonical module. Since
![]() $\Omega ^{d-1}_R k$
has co-depth
$\Omega ^{d-1}_R k$
has co-depth
![]() $1$
, by [Reference Leuschke and Wiegand27, Prop. 11.21] (see 5.1.5), we get that
$1$
, by [Reference Leuschke and Wiegand27, Prop. 11.21] (see 5.1.5), we get that
![]() $0\to \omega _R \to E^R \to \Omega ^{d-1}_Rk \to 0$
is the minimal MCM approximation of
$0\to \omega _R \to E^R \to \Omega ^{d-1}_Rk \to 0$
is the minimal MCM approximation of
![]() $\Omega ^{d-1}_R k$
. Now, pick an R-regular element
$\Omega ^{d-1}_R k$
. Now, pick an R-regular element
![]() $x\in \mathfrak {m}\setminus \mathfrak {m}^2$
(which is also
$x\in \mathfrak {m}\setminus \mathfrak {m}^2$
(which is also
![]() $\Omega ^{d-1}_R k$
-regular, since
$\Omega ^{d-1}_R k$
-regular, since
![]() $d-1>0$
). By [Reference Yoshida39, Cor. 2.5], we have
$d-1>0$
). By [Reference Yoshida39, Cor. 2.5], we have
![]() $0\to \omega _{R/xR}\to E^R/xE^R\to \Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk)\to 0$
is the minimal MCM approximation of
$0\to \omega _{R/xR}\to E^R/xE^R\to \Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk)\to 0$
is the minimal MCM approximation of
![]() $\Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk) \cong \Omega ^{d-1}_{R/xR}k \oplus \Omega ^{d-2}_{R/xR} k$
over
$\Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk) \cong \Omega ^{d-1}_{R/xR}k \oplus \Omega ^{d-2}_{R/xR} k$
over
![]() $R/xR$
(the isomorphism follows from [Reference Takahashi37, Cor. 5.3]). Since
$R/xR$
(the isomorphism follows from [Reference Takahashi37, Cor. 5.3]). Since
![]() $0\to 0 \to \Omega ^{d-1}_{R/xR}k\to \Omega ^{d-1}_{R/xR}k \to 0$
is the minimal MCM approximation of
$0\to 0 \to \Omega ^{d-1}_{R/xR}k\to \Omega ^{d-1}_{R/xR}k \to 0$
is the minimal MCM approximation of
![]() $\Omega ^{d-1}_{R/xR}k$
over
$\Omega ^{d-1}_{R/xR}k$
over
![]() $R/xR$
and
$R/xR$
and
![]() $0\to \omega _{R/xR}\to E^{R/xR} \to \Omega ^{d-2}_{R/xR} k \to 0$
is the minimal MCM approximation of
$0\to \omega _{R/xR}\to E^{R/xR} \to \Omega ^{d-2}_{R/xR} k \to 0$
is the minimal MCM approximation of
![]() $\Omega ^{d-2}_{R/xR} k$
over
$\Omega ^{d-2}_{R/xR} k$
over
![]() $R/xR$
(by 5.1.5 and [Reference Leuschke and Wiegand27, Prop. 11.21]), their direct sum
$R/xR$
(by 5.1.5 and [Reference Leuschke and Wiegand27, Prop. 11.21]), their direct sum
![]() $0\to \omega _{R/xR}\to E^{R/xR} \oplus \Omega ^{d-1}_{R/xR}k \to \Omega ^{d-2}_{R/xR} k \oplus \Omega ^{d-1}_{R/xR}k \to 0$
is the minimal MCM approximation of
$0\to \omega _{R/xR}\to E^{R/xR} \oplus \Omega ^{d-1}_{R/xR}k \to \Omega ^{d-2}_{R/xR} k \oplus \Omega ^{d-1}_{R/xR}k \to 0$
is the minimal MCM approximation of
![]() $\Omega ^{d-2}_{R/xR} k \oplus \Omega ^{d-1}_{R/xR}k\cong \Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk)$
over
$\Omega ^{d-2}_{R/xR} k \oplus \Omega ^{d-1}_{R/xR}k\cong \Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk)$
over
![]() $R/xR$
(direct sum preserves minimal MCM approximation by [Reference Yoshida39, Th. 1.4]). By uniqueness of minimal MCM approximation, we have
$R/xR$
(direct sum preserves minimal MCM approximation by [Reference Yoshida39, Th. 1.4]). By uniqueness of minimal MCM approximation, we have
![]() $E^R/xE^R\cong E^{R/xR} \oplus \Omega ^{d-1}_{R/xR}k$
. So,
$E^R/xE^R\cong E^{R/xR} \oplus \Omega ^{d-1}_{R/xR}k$
. So,
![]() $\mu _R(E^R)=\mu _{R/xR}(E^R/xE^R)=\mu _{R/xR}(E^{R/xR})+\mu _{R/xR}(\Omega ^{d-1}_{R/xR}k)$
. Since R is not regular,
$\mu _R(E^R)=\mu _{R/xR}(E^R/xE^R)=\mu _{R/xR}(E^{R/xR})+\mu _{R/xR}(\Omega ^{d-1}_{R/xR}k)$
. Since R is not regular,
![]() $R/xR$
is not regular. Hence, by induction hypothesis, we have
$R/xR$
is not regular. Hence, by induction hypothesis, we have
![]() $\mu _{R/xR}(E^{R/xR})=\text {r}(R/xR)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k)=\text {r}(R)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k)$
. So,
$\mu _{R/xR}(E^{R/xR})=\text {r}(R/xR)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k)=\text {r}(R)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k)$
. So,
 $\mu _R(E^R)=\text {r}(R)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k)+\mu _{R/xR}(\Omega ^{d-1}_{R/xR} k)=\text {r}(R)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k \oplus \Omega ^{d-1}_{R/xR}k)=\text {r}(R)+\mu _{R/xR}\left ( \Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk) \right )=\text {r}(R)+\mu _R(\Omega ^{d-1}_R k)$
. This finishes the inductive step, and hence the proof.
$\mu _R(E^R)=\text {r}(R)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k)+\mu _{R/xR}(\Omega ^{d-1}_{R/xR} k)=\text {r}(R)+\mu _{R/xR}(\Omega ^{d-2}_{R/xR} k \oplus \Omega ^{d-1}_{R/xR}k)=\text {r}(R)+\mu _{R/xR}\left ( \Omega ^{d-1}_R k/x(\Omega ^{d-1}_Rk) \right )=\text {r}(R)+\mu _R(\Omega ^{d-1}_R k)$
. This finishes the inductive step, and hence the proof.
Since
![]() $\mu (\omega _R)=\text {r}(R)$
, Lemma 5.1.8 says that the sequence
$\mu (\omega _R)=\text {r}(R)$
, Lemma 5.1.8 says that the sequence
![]() $0\to \omega _R\to E^R\to \Omega _R^{d-1}k\to 0$
is
$0\to \omega _R\to E^R\to \Omega _R^{d-1}k\to 0$
is
![]() $\mu $
-additive. As a consequence of this, we get the following.
$\mu $
-additive. As a consequence of this, we get the following.
Proposition 5.1.9. Let
![]() $(R,\mathfrak {m},k)$
be a non-regular local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m},k)$
be a non-regular local Cohen–Macaulay ring of dimension
![]() $d\ge 1$
, and let N be a finitely generated nonzero R-module with finite injective dimension. Then
$d\ge 1$
, and let N be a finitely generated nonzero R-module with finite injective dimension. Then
![]() ${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }={\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)\ne 0$
.
${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }={\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)\ne 0$
.
Proof. That
![]() ${\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)\cong {\operatorname{Ext}}^d_R(k,N)\ne 0$
follows from [Reference Bruns and Herzog3, Exer. 3.1.24]. So, it is enough to prove that
${\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)\cong {\operatorname{Ext}}^d_R(k,N)\ne 0$
follows from [Reference Bruns and Herzog3, Exer. 3.1.24]. So, it is enough to prove that
![]() ${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }={\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)$
.
${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }={\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)$
.
We first consider the case where R is complete, hence admitting a canonical module
![]() $\omega _R$
. Consider the
$\omega _R$
. Consider the
![]() $\mu $
-additive (by Lemma 5.1.8) exact sequence
$\mu $
-additive (by Lemma 5.1.8) exact sequence
![]() $\sigma :0\to \omega _R\to E^R\to \Omega _R^{d-1}k\to 0$
. Since
$\sigma :0\to \omega _R\to E^R\to \Omega _R^{d-1}k\to 0$
. Since
![]() $\sigma \in {\cal{S}}|_{{\operatorname{mod}}\ R}^{\mu }$
, by applying
$\sigma \in {\cal{S}}|_{{\operatorname{mod}}\ R}^{\mu }$
, by applying
![]() $\operatorname{Hom}_R(-,N)$
to
$\operatorname{Hom}_R(-,N)$
to
![]() $\sigma $
, we get the following part of a commutative diagram of exact sequences by Corollary 3.9:
$\sigma $
, we get the following part of a commutative diagram of exact sequences by Corollary 3.9:

Since
![]() $E^R$
is maximal Cohen–Macaulay, we have
$E^R$
is maximal Cohen–Macaulay, we have
![]() ${\operatorname{Ext}}_{R}^1(E^R,N)=0$
by [Reference Bruns and Herzog3, Exer. 3.1.24]. So,
${\operatorname{Ext}}_{R}^1(E^R,N)=0$
by [Reference Bruns and Herzog3, Exer. 3.1.24]. So,
![]() ${\operatorname{Ext}}_{R}^1(E^R,N)^{\mu }=0$
as well. Hence, we get the following commutative diagram:
${\operatorname{Ext}}_{R}^1(E^R,N)^{\mu }=0$
as well. Hence, we get the following commutative diagram:

Thus,
![]() $h\circ g=f$
is surjective, so h is surjective. Since h is the natural inclusion map, we have
$h\circ g=f$
is surjective, so h is surjective. Since h is the natural inclusion map, we have
![]() ${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }={\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)$
.
${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }={\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)$
.
Now, we consider the general case. Since
![]() ${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }\subseteq {\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)$
, it is enough to prove the other inclusion. So, let
${\operatorname{Ext}}^1_R(\Omega _R^{d-1}k,N)^{\mu }\subseteq {\operatorname{Ext}}_{R}^1(\Omega _R^{d-1}k,N)$
, it is enough to prove the other inclusion. So, let
![]() $\sigma : 0\to N\to X\to \Omega ^{d-1}_R k\to 0 $
be a short exact sequence. We need to show that
$\sigma : 0\to N\to X\to \Omega ^{d-1}_R k\to 0 $
be a short exact sequence. We need to show that
![]() $\sigma $
is
$\sigma $
is
![]() $\mu $
-additive. Now, consider the completion
$\mu $
-additive. Now, consider the completion
![]() $\widehat \sigma : 0\to \widehat N\to \widehat X\to \widehat {\Omega ^{d-1}_R k}\cong \Omega ^{d-1}_{\widehat R} k \to 0$
. Since
$\widehat \sigma : 0\to \widehat N\to \widehat X\to \widehat {\Omega ^{d-1}_R k}\cong \Omega ^{d-1}_{\widehat R} k \to 0$
. Since
![]() $\widehat R$
is non-regular, Cohen–Macaulay of dimension d admits a canonical module, and
$\widehat R$
is non-regular, Cohen–Macaulay of dimension d admits a canonical module, and
![]() $\widehat N \in {\operatorname{mod}} \widehat R$
has finite injective dimension over
$\widehat N \in {\operatorname{mod}} \widehat R$
has finite injective dimension over
![]() $\widehat R$
, by the first part of the proof, we get
$\widehat R$
, by the first part of the proof, we get
![]() $ {\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)={\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)^{\mu }$
. Thus,
$ {\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)={\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)^{\mu }$
. Thus,
![]() $[\widehat \sigma ]\in {\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)={\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)^{\mu }$
. Hence,
$[\widehat \sigma ]\in {\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)={\operatorname{Ext}}^1_{\widehat R}(\Omega ^{d-1}_{\widehat R} k,\widehat N)^{\mu }$
. Hence,
![]() $\widehat \sigma $
is
$\widehat \sigma $
is
![]() $\mu $
-additive. So,
$\mu $
-additive. So,
![]() $\mu _{\widehat R}(\widehat N)+\mu _{\widehat R}( \Omega ^{d-1}_{\widehat R} k)=\mu _{\widehat R}(\widehat X)$
. Since the number of generators does not change under completion, we get
$\mu _{\widehat R}(\widehat N)+\mu _{\widehat R}( \Omega ^{d-1}_{\widehat R} k)=\mu _{\widehat R}(\widehat X)$
. Since the number of generators does not change under completion, we get
![]() $\mu _R(N)+\mu _R(\Omega ^{d-1}_R k)=\mu _R(X)$
. Thus,
$\mu _R(N)+\mu _R(\Omega ^{d-1}_R k)=\mu _R(X)$
. Thus,
![]() $\sigma $
is
$\sigma $
is
![]() $\mu $
-additive, which is what we wanted to prove.
$\mu $
-additive, which is what we wanted to prove.
For an arbitrary local ring of positive depth, we give a characterization of the ring being regular in terms of vanishing of
![]() ${\operatorname{Ext}}^1_R(k,M)^{\mu }$
for some
${\operatorname{Ext}}^1_R(k,M)^{\mu }$
for some
![]() $M\in {\operatorname{mod}}\ R$
of finite projective dimension. For this, we first recall the definitions of weakly
$M\in {\operatorname{mod}}\ R$
of finite projective dimension. For this, we first recall the definitions of weakly
![]() $\mathfrak {m}$
-full and Burch submodules of a module from [Reference Dey and Kobayashi12, Defs. 3.1 and 4.1] and subsequently, we relate that property to the vanishing of certain
$\mathfrak {m}$
-full and Burch submodules of a module from [Reference Dey and Kobayashi12, Defs. 3.1 and 4.1] and subsequently, we relate that property to the vanishing of certain
![]() ${\operatorname{Ext}}^1_R(k,-)^{\mu }$
.
${\operatorname{Ext}}^1_R(k,-)^{\mu }$
.
Definition 5.1.10. Let
![]() $(R,\mathfrak {m},k)$
be a local ring, and let N be an R-submodule of a finitely generated R-module M. Then N is called a weakly
$(R,\mathfrak {m},k)$
be a local ring, and let N be an R-submodule of a finitely generated R-module M. Then N is called a weakly
![]() $\mathfrak {m}$
-full submodule of M if
$\mathfrak {m}$
-full submodule of M if
![]() $(\mathfrak {m} N:_M\mathfrak {m})=N$
. Also, N is called a Burch submodule of M if
$(\mathfrak {m} N:_M\mathfrak {m})=N$
. Also, N is called a Burch submodule of M if
![]() $\mathfrak {m} (N:_M \mathfrak {m})\ne \mathfrak {m} N$
.
$\mathfrak {m} (N:_M \mathfrak {m})\ne \mathfrak {m} N$
.
Proposition 5.1.11. Let
![]() $(R,\mathfrak {m},k)$
be a local ring, and let N be an R-submodule of a finitely generated R-module M such that
$(R,\mathfrak {m},k)$
be a local ring, and let N be an R-submodule of a finitely generated R-module M such that
![]() ${\operatorname{Ext}}^1_R(k,N)^{\mu }=0$
. Then
${\operatorname{Ext}}^1_R(k,N)^{\mu }=0$
. Then
![]() $(\mathfrak {m} N:_M\mathfrak {m})=N+\operatorname{Soc}(M)$
, that is,
$(\mathfrak {m} N:_M\mathfrak {m})=N+\operatorname{Soc}(M)$
, that is,
![]() $N+\operatorname{Soc}(M)$
is a weakly
$N+\operatorname{Soc}(M)$
is a weakly
![]() $\mathfrak {m}$
-full submodule of M. So, in particular, if we moreover have
$\mathfrak {m}$
-full submodule of M. So, in particular, if we moreover have
![]() $\operatorname{depth}(M)>0$
, then N is a weakly
$\operatorname{depth}(M)>0$
, then N is a weakly
![]() $\mathfrak {m}$
-full submodule of M.
$\mathfrak {m}$
-full submodule of M.
Proof. Clearly,
![]() $N\subseteq (\mathfrak {m} N:_M \mathfrak {m})$
and
$N\subseteq (\mathfrak {m} N:_M \mathfrak {m})$
and
![]() $\operatorname{Soc}(M)=(0:_M \mathfrak {m})\subseteq (\mathfrak {m} N:_M\mathfrak {m})$
, so
$\operatorname{Soc}(M)=(0:_M \mathfrak {m})\subseteq (\mathfrak {m} N:_M\mathfrak {m})$
, so
![]() $N+\operatorname{Soc}(M)\subseteq (\mathfrak {m} N:_M\mathfrak {m})$
. Now, choose an element
$N+\operatorname{Soc}(M)\subseteq (\mathfrak {m} N:_M\mathfrak {m})$
. Now, choose an element
![]() $f\in (\mathfrak {m} N:_M\mathfrak {m})$
, and we aim to show
$f\in (\mathfrak {m} N:_M\mathfrak {m})$
, and we aim to show
![]() $f\in N+\operatorname{Soc}(M)$
. If
$f\in N+\operatorname{Soc}(M)$
. If
![]() $f\in N$
, then we are done. Otherwise, say
$f\in N$
, then we are done. Otherwise, say
![]() $f\notin N$
. As
$f\notin N$
. As
![]() $f\in (\mathfrak {m} N:_M\mathfrak {m})$
, so
$f\in (\mathfrak {m} N:_M\mathfrak {m})$
, so
![]() $\mathfrak {m} f\subseteq \mathfrak {m} N\subseteq N$
, and hence
$\mathfrak {m} f\subseteq \mathfrak {m} N\subseteq N$
, and hence
![]() $\mathfrak {m}(N+Rf)=\mathfrak {m} N$
. Thus,
$\mathfrak {m}(N+Rf)=\mathfrak {m} N$
. Thus,
![]() $\dfrac {Rf+N}{N}$
is a nonzero (as
$\dfrac {Rf+N}{N}$
is a nonzero (as
![]() $f\not \in N$
) k-vector space (as
$f\not \in N$
) k-vector space (as
![]() $\mathfrak {m}(N+Rf)\subseteq N$
). Moreover,
$\mathfrak {m}(N+Rf)\subseteq N$
). Moreover,
![]() $\dfrac {Rf+N}{N}$
is cyclically generated by the image of f in
$\dfrac {Rf+N}{N}$
is cyclically generated by the image of f in
![]() $M/N$
. Hence,
$M/N$
. Hence,
![]() $\dfrac {Rf+N}{N}\cong k$
, so we have a short exact sequence
$\dfrac {Rf+N}{N}\cong k$
, so we have a short exact sequence
![]() $\sigma : 0\to N\to Rf+N \to k\to 0$
. This sequence is
$\sigma : 0\to N\to Rf+N \to k\to 0$
. This sequence is
![]() $\mu $
-additive, since
$\mu $
-additive, since
 $\mu (N+Rf)=\lambda \left (\frac {N+Rf}{\mathfrak {m}(N+Rf)}\right )=\lambda \left (\frac {N+Rf}{\mathfrak {m} N}\right )=\lambda \left (\frac {N+Rf}{N}\right )+\lambda \left (\frac {N}{\mathfrak {m} N}\right )=\lambda (k)+\mu (N)=\mu (k)+\mu (N)$
. So,
$\mu (N+Rf)=\lambda \left (\frac {N+Rf}{\mathfrak {m}(N+Rf)}\right )=\lambda \left (\frac {N+Rf}{\mathfrak {m} N}\right )=\lambda \left (\frac {N+Rf}{N}\right )+\lambda \left (\frac {N}{\mathfrak {m} N}\right )=\lambda (k)+\mu (N)=\mu (k)+\mu (N)$
. So,
![]() $\sigma \in {\operatorname{Ext}}^1_R(k,N)^{\mu }=0$
. Hence,
$\sigma \in {\operatorname{Ext}}^1_R(k,N)^{\mu }=0$
. Hence,
![]() $\sigma $
splits. Thus,
$\sigma $
splits. Thus,
![]() $N+Rf=N\oplus g(k)$
, where
$N+Rf=N\oplus g(k)$
, where
![]() $g:k\to N+Rf$
is the splitting map, so
$g:k\to N+Rf$
is the splitting map, so
![]() $k\cong g(k)$
. Now,
$k\cong g(k)$
. Now,
![]() $f\in N+Rf=N\oplus g(k)$
, so
$f\in N+Rf=N\oplus g(k)$
, so
![]() $f=x+y$
for some
$f=x+y$
for some
![]() $x\in N$
and
$x\in N$
and
![]() $y\in g(k)\subseteq M$
. Since
$y\in g(k)\subseteq M$
. Since
![]() $k\cong g(k)$
, we have
$k\cong g(k)$
, we have
![]() $\mathfrak {m} g(k)=0$
. Now,
$\mathfrak {m} g(k)=0$
. Now,
![]() $\mathfrak {m} y\in \mathfrak {m} g(k)=0$
, so
$\mathfrak {m} y\in \mathfrak {m} g(k)=0$
, so
![]() $y\in (0:_M\mathfrak {m})=\operatorname{Soc}(M)$
. Hence,
$y\in (0:_M\mathfrak {m})=\operatorname{Soc}(M)$
. Hence,
![]() $f=x+y\in N+\operatorname{Soc}(M)$
. This finally shows that
$f=x+y\in N+\operatorname{Soc}(M)$
. This finally shows that
![]() $(\mathfrak {m} N:_M\mathfrak {m})\subseteq N+\operatorname{Soc}(M)$
, so
$(\mathfrak {m} N:_M\mathfrak {m})\subseteq N+\operatorname{Soc}(M)$
, so
![]() $(\mathfrak {m} N:_M\mathfrak {m})=N+\operatorname{Soc}(M)$
. Since
$(\mathfrak {m} N:_M\mathfrak {m})=N+\operatorname{Soc}(M)$
. Since
![]() $\mathfrak {m}(N+\operatorname{Soc}(M))=\mathfrak {m} N$
, we get
$\mathfrak {m}(N+\operatorname{Soc}(M))=\mathfrak {m} N$
, we get
![]() $(\mathfrak {m} (N+\operatorname{Soc}(M)):_M\mathfrak {m})=N+\operatorname{Soc}(M)$
, which implies that
$(\mathfrak {m} (N+\operatorname{Soc}(M)):_M\mathfrak {m})=N+\operatorname{Soc}(M)$
, which implies that
![]() $N+\operatorname{Soc}(M)$
is a weakly
$N+\operatorname{Soc}(M)$
is a weakly
![]() $\mathfrak {m}$
-full submodule M. Now note that if
$\mathfrak {m}$
-full submodule M. Now note that if
![]() $\operatorname{depth}(M)>0$
, then
$\operatorname{depth}(M)>0$
, then
![]() $\operatorname{Soc}(M)=0$
. Hence,
$\operatorname{Soc}(M)=0$
. Hence,
![]() $N+\operatorname{Soc}(M)=N$
is a weakly
$N+\operatorname{Soc}(M)=N$
is a weakly
![]() $\mathfrak {m}$
-full submodule of M.
$\mathfrak {m}$
-full submodule of M.
Now, we give another characterization of regular local rings in terms of vanishing of certain
![]() ${\operatorname{Ext}}^1_R(k,-)^{\mu }$
.
${\operatorname{Ext}}^1_R(k,-)^{\mu }$
.
Theorem 5.1.12. Let
![]() $(R,\mathfrak {m},k)$
be a local ring of depth
$(R,\mathfrak {m},k)$
be a local ring of depth
![]() $t>0$
. Then, the following are equivalent:
$t>0$
. Then, the following are equivalent:
-
(1) R is regular.
-
(2)
 ${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)^{\mu }=0$
for some R-regular sequence
${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)^{\mu }=0$
for some R-regular sequence
 $x_1,...,x_{t-1}$
.
$x_1,...,x_{t-1}$
. -
(3)
 ${\operatorname{Ext}}^1_R(k,M)^{\mu }=0$
for some finitely generated R-module M of projective dimension
${\operatorname{Ext}}^1_R(k,M)^{\mu }=0$
for some finitely generated R-module M of projective dimension
 $t-1$
.
$t-1$
.
Proof.
![]() $(1) \implies (2)$
Since R is regular, we have
$(1) \implies (2)$
Since R is regular, we have
![]() $t=\dim R$
. Since R is regular, we get that
$t=\dim R$
. Since R is regular, we get that
![]() $\mathfrak {m}$
is generated by a regular sequence
$\mathfrak {m}$
is generated by a regular sequence
![]() $x_1,...,x_t$
. Now,
$x_1,...,x_t$
. Now,
![]() $R/(x_1,...,x_{t-1})R$
has projective dimension
$R/(x_1,...,x_{t-1})R$
has projective dimension
![]() $t-1$
over R and the
$t-1$
over R and the
![]() $(t-1)$
th Betti number of this module is
$(t-1)$
th Betti number of this module is
![]() $1$
(by looking at the Koszul complex). Hence,
$1$
(by looking at the Koszul complex). Hence,
![]() ${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)\cong \operatorname{Tor}^R_{t-1}(k,R/(x_1,...,x_{t-1})R)\cong k$
by [Reference Bruns and Herzog3, Exer. 3.3.26]. Now, we have an exact sequence
${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)\cong \operatorname{Tor}^R_{t-1}(k,R/(x_1,...,x_{t-1})R)\cong k$
by [Reference Bruns and Herzog3, Exer. 3.3.26]. Now, we have an exact sequence
![]() $0\to R/(x_1,...,x_{t-1})R\xrightarrow {\cdot x_t} R/(x_1,...,x_{t-1})R\to R/(x_1,...,x_{t-1},x_t)R\cong k\to 0$
, which is clearly not
$0\to R/(x_1,...,x_{t-1})R\xrightarrow {\cdot x_t} R/(x_1,...,x_{t-1})R\to R/(x_1,...,x_{t-1},x_t)R\cong k\to 0$
, which is clearly not
![]() $\mu $
-additive. Hence,
$\mu $
-additive. Hence,
![]() ${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)\ne {\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)^{\mu }$
. Since
${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)\ne {\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)^{\mu }$
. Since
![]() ${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)\cong k$
is cyclic, by Lemma 5.1.2, we get that
${\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)\cong k$
is cyclic, by Lemma 5.1.2, we get that
![]() ${\operatorname{Ext}}^1_R(k,R/(x_1,..., x_{t-1})R)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)=0$
.
${\operatorname{Ext}}^1_R(k,R/(x_1,..., x_{t-1})R)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(k,R/(x_1,...,x_{t-1})R)=0$
.
![]() $(2) \implies (3)$
Obvious.
$(2) \implies (3)$
Obvious.
![]() $(3) \implies (1)$
By the Auslander–Buchsbaum formula,
$(3) \implies (1)$
By the Auslander–Buchsbaum formula,
![]() $\operatorname{depth}\ M=1$
, so
$\operatorname{depth}\ M=1$
, so
![]() $\operatorname{Soc}(M)=0$
. Hence, by prime avoidance, we can choose
$\operatorname{Soc}(M)=0$
. Hence, by prime avoidance, we can choose
![]() $x\in \mathfrak {m}$
, which is both R and M-regular. Then
$x\in \mathfrak {m}$
, which is both R and M-regular. Then
![]() $xM\cong M$
, so
$xM\cong M$
, so
![]() ${\operatorname{Ext}}^1_R(k, xM)^{\mu }\cong {\operatorname{Ext}}^1_R(k,M)^{\mu }=0$
. By Proposition 5.1.11, we get that
${\operatorname{Ext}}^1_R(k, xM)^{\mu }\cong {\operatorname{Ext}}^1_R(k,M)^{\mu }=0$
. By Proposition 5.1.11, we get that
![]() $xM$
is a weakly
$xM$
is a weakly
![]() $\mathfrak {m}$
-full submodule of M. Since
$\mathfrak {m}$
-full submodule of M. Since
![]() $\operatorname{depth} (M/xM)=0$
,
$\operatorname{depth} (M/xM)=0$
,
![]() $xM$
is a Burch submodule of M by [Reference Dey and Kobayashi12, Lem. 4.3]. Moreover,
$xM$
is a Burch submodule of M by [Reference Dey and Kobayashi12, Lem. 4.3]. Moreover,
![]() $\operatorname{pd}_{R/xR}(M/xM)=\operatorname{pd}_R M<\infty $
, and
$\operatorname{pd}_{R/xR}(M/xM)=\operatorname{pd}_R M<\infty $
, and
![]() $\operatorname{pd}_R R/xR <\infty $
, so
$\operatorname{pd}_R R/xR <\infty $
, so
![]() $\operatorname{pd}_R M/xM<\infty $
. Hence,
$\operatorname{pd}_R M/xM<\infty $
. Hence,
![]() $\operatorname{Tor}^R_{\gg 0}(k,M/xM)=0$
. Thus,
$\operatorname{Tor}^R_{\gg 0}(k,M/xM)=0$
. Thus,
![]() $\operatorname{pd}_R k<\infty $
by [Reference Dey and Kobayashi12, Th. 1.2], so R is regular.
$\operatorname{pd}_R k<\infty $
by [Reference Dey and Kobayashi12, Th. 1.2], so R is regular.
Next, we try to relate
![]() ${\operatorname{Ext}}^1_R(M,N)^{\mu }$
to
${\operatorname{Ext}}^1_R(M,N)^{\mu }$
to
![]() ${\operatorname{Ext}}^1_R(M,N)$
for all
${\operatorname{Ext}}^1_R(M,N)$
for all
![]() $M,N\in {\operatorname{mod}}\ R$
, when
$M,N\in {\operatorname{mod}}\ R$
, when
![]() $(R,\mathfrak {m})$
is a regular local ring of dimension
$(R,\mathfrak {m})$
is a regular local ring of dimension
![]() $1$
(i.e., a local PID). For this, we first record a preliminary lemma.
$1$
(i.e., a local PID). For this, we first record a preliminary lemma.
Lemma 5.1.13. Let
![]() $(R,\mathfrak {m})$
be a local ring, and let
$(R,\mathfrak {m})$
be a local ring, and let
![]() $x\in \mathfrak {m}$
be a nonzero divisor. Then,
$x\in \mathfrak {m}$
be a nonzero divisor. Then,
![]() ${\operatorname{Ext}}^1_R(R/xR, R/I)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R/xR, R/I)\cong \dfrac {\mathfrak {m}}{I+xR}$
for every proper ideal I of R.
${\operatorname{Ext}}^1_R(R/xR, R/I)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R/xR, R/I)\cong \dfrac {\mathfrak {m}}{I+xR}$
for every proper ideal I of R.
Proof. Calculating
![]() ${\operatorname{Ext}}^1_R(R/xR, R/I)$
from the minimal free-resolution
${\operatorname{Ext}}^1_R(R/xR, R/I)$
from the minimal free-resolution
![]() $0\to R \xrightarrow {\cdot x} R\to R/xR\to 0$
of
$0\to R \xrightarrow {\cdot x} R\to R/xR\to 0$
of
![]() $R/xR$
, we see that
$R/xR$
, we see that
![]() ${\operatorname{Ext}}^1_R(R/xR,R/I)\cong R/(xR+I)$
is a cyclic R-module. By Lemma 5.2.1, we have
${\operatorname{Ext}}^1_R(R/xR,R/I)\cong R/(xR+I)$
is a cyclic R-module. By Lemma 5.2.1, we have
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(R/xR,R/I)\subseteq {\operatorname{Ext}}^1_R(R/xR,R/I)^{\mu }$
. We finally claim that
$\mathfrak {m}{\operatorname{Ext}}^1_R(R/xR,R/I)\subseteq {\operatorname{Ext}}^1_R(R/xR,R/I)^{\mu }$
. We finally claim that
![]() ${\operatorname{Ext}}^1_R(R/xR,R/I)^{\mu }\neq {\operatorname{Ext}}^1_R(R/xR,R/I)$
. Indeed, we have an exact sequence
${\operatorname{Ext}}^1_R(R/xR,R/I)^{\mu }\neq {\operatorname{Ext}}^1_R(R/xR,R/I)$
. Indeed, we have an exact sequence
![]() $\sigma : 0\to xR/xI \to R/xI\to R/xR\to 0$
. Now, we have a natural surjection
$\sigma : 0\to xR/xI \to R/xI\to R/xR\to 0$
. Now, we have a natural surjection
![]() $R \xrightarrow {r\mapsto rx+xI} xR/xI$
, whose kernel is
$R \xrightarrow {r\mapsto rx+xI} xR/xI$
, whose kernel is
![]() $\{r\in R: rx\in xI\}$
. Since x is a nonzero divisor,
$\{r\in R: rx\in xI\}$
. Since x is a nonzero divisor,
![]() $rx\in xI$
if and only if
$rx\in xI$
if and only if
![]() $r\in I$
. Hence, the kernel is I. Hence,
$r\in I$
. Hence, the kernel is I. Hence,
![]() $R/I\cong xR/xI$
. So, we get the exact sequence
$R/I\cong xR/xI$
. So, we get the exact sequence
![]() $\sigma : 0\to R/I\to R/xI \to R/xR\to 0$
. Moreover,
$\sigma : 0\to R/I\to R/xI \to R/xR\to 0$
. Moreover,
![]() $\sigma $
is not
$\sigma $
is not
![]() $\mu $
-additive, since
$\mu $
-additive, since
![]() $\mu (R/xI)=1\ne 1+1= \mu (R/I)+\mu (R/xR)$
. Thus,
$\mu (R/xI)=1\ne 1+1= \mu (R/I)+\mu (R/xR)$
. Thus,
![]() $[\sigma ]\in {\operatorname{Ext}}^1_R(R/xR, R/I)\setminus {\operatorname{Ext}}^1_R(R/xR, R/I)^{\mu }$
. Hence,
$[\sigma ]\in {\operatorname{Ext}}^1_R(R/xR, R/I)\setminus {\operatorname{Ext}}^1_R(R/xR, R/I)^{\mu }$
. Hence,
![]() ${\operatorname{Ext}}^1_R(R/xR,R/I)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(R/xR,R/I)$
by Lemma 5.1.2.
${\operatorname{Ext}}^1_R(R/xR,R/I)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(R/xR,R/I)$
by Lemma 5.1.2.
Now, using this lemma, we can compare the structure of
![]() ${\operatorname{Ext}}^1_R(M,N)^{\mu }$
to
${\operatorname{Ext}}^1_R(M,N)^{\mu }$
to
![]() ${\operatorname{Ext}}^1_R(M,N)$
for every pair of finitely generated modules
${\operatorname{Ext}}^1_R(M,N)$
for every pair of finitely generated modules
![]() $M,N$
over a DVR.
$M,N$
over a DVR.
Proposition 5.1.14. Let
![]() $(R,\mathfrak {m})$
be a regular local ring of dimension
$(R,\mathfrak {m})$
be a regular local ring of dimension
![]() $1$
. Then,
$1$
. Then,
![]() ${\operatorname{Ext}}^1_R(M,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
for all finitely generated R-modules M and N. So, in particular,
${\operatorname{Ext}}^1_R(M,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
for all finitely generated R-modules M and N. So, in particular,
![]() ${\operatorname{Ext}}^1_R(k,N)^{\mu }=0$
for all finitely generated R-modules N.
${\operatorname{Ext}}^1_R(k,N)^{\mu }=0$
for all finitely generated R-modules N.
Proof. Let
![]() $\mathfrak {m}=xR$
. Then, for every finitely generated R-module X, we have
$\mathfrak {m}=xR$
. Then, for every finitely generated R-module X, we have
![]() $X\cong R^{\oplus a}\oplus \left (\oplus _{i=1}^n R/x^{a_i}R\right )$
for some nonnegative integers (depending on X)
$X\cong R^{\oplus a}\oplus \left (\oplus _{i=1}^n R/x^{a_i}R\right )$
for some nonnegative integers (depending on X)
![]() $a,a_i$
. Now, fix arbitrary
$a,a_i$
. Now, fix arbitrary
![]() $N\in {\operatorname{mod}}\ R$
. Applying Lemma 2.4 to the subfunctor
$N\in {\operatorname{mod}}\ R$
. Applying Lemma 2.4 to the subfunctor
![]() ${\operatorname{Ext}}^1_R(-,N)^{\mu }$
of
${\operatorname{Ext}}^1_R(-,N)^{\mu }$
of
![]() ${\operatorname{Ext}}^1_R(-,N)$
and taking
${\operatorname{Ext}}^1_R(-,N)$
and taking
![]() $I=\mathfrak {m}$
, it is enough to prove that
$I=\mathfrak {m}$
, it is enough to prove that
![]() ${\operatorname{Ext}}^1_R(R,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R,N)$
and
${\operatorname{Ext}}^1_R(R,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R,N)$
and
![]() ${\operatorname{Ext}}^1_R(R/x^lR,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R/x^lR,N)$
for every integer
${\operatorname{Ext}}^1_R(R/x^lR,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R/x^lR,N)$
for every integer
![]() $l\ge 1$
. Now,
$l\ge 1$
. Now,
![]() ${\operatorname{Ext}}^1_R(R,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R,N)$
is obvious, as both sides are zero. Now, to prove
${\operatorname{Ext}}^1_R(R,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R,N)$
is obvious, as both sides are zero. Now, to prove
![]() ${\operatorname{Ext}}^1_R(R/x^lR,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R/x^lR,N)$
for every integer
${\operatorname{Ext}}^1_R(R/x^lR,N)^{\mu }=\mathfrak {m}{\operatorname{Ext}}^1_R(R/x^lR,N)$
for every integer
![]() $l\ge 1$
, first fix an
$l\ge 1$
, first fix an
![]() $l\ge 1$
, and look at the subfunctor
$l\ge 1$
, and look at the subfunctor
![]() ${\operatorname{Ext}}^1_R(R/x^lR,-)^{\mu }$
of
${\operatorname{Ext}}^1_R(R/x^lR,-)^{\mu }$
of
![]() ${\operatorname{Ext}}^1_R(R/x^lR,-)$
. Again, by the structure of finitely generated R-modules and Lemma 2.4, it is enough to prove that
${\operatorname{Ext}}^1_R(R/x^lR,-)$
. Again, by the structure of finitely generated R-modules and Lemma 2.4, it is enough to prove that
![]() ${\operatorname{Ext}}^1_R(R/x^lR,R)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(R/x^lR,R)$
and
${\operatorname{Ext}}^1_R(R/x^lR,R)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(R/x^lR,R)$
and
![]() ${\operatorname{Ext}}^1_R(R/x^lR,R/x^bR)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(R/x^lR,R/x^bR)$
for every integer
${\operatorname{Ext}}^1_R(R/x^lR,R/x^bR)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(R/x^lR,R/x^bR)$
for every integer
![]() $b\ge 1$
. Now, these equalities follow from Lemma 5.1.13, since x is a nonzero divisor.
$b\ge 1$
. Now, these equalities follow from Lemma 5.1.13, since x is a nonzero divisor.
When restricting to short exact sequences in
![]() ${\operatorname{Ext}}^1$
, on which certain subadditive function, other than
${\operatorname{Ext}}^1$
, on which certain subadditive function, other than
![]() $\mu (-)$
, is additive, one obtains vanishing of the corresponding submodule of
$\mu (-)$
, is additive, one obtains vanishing of the corresponding submodule of
![]() ${\operatorname{Ext}}^1_R(M,F)$
for any free R-module F. We make this precise in Proposition 5.1.16, whose proof uses the following lemma.
${\operatorname{Ext}}^1_R(M,F)$
for any free R-module F. We make this precise in Proposition 5.1.16, whose proof uses the following lemma.
Lemma 5.1.15. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let
$1$
. Let
![]() $x\in \mathfrak {m}$
be R-regular. Let
$x\in \mathfrak {m}$
be R-regular. Let
![]() $\sigma :0\to F_1\to F_2\oplus \frac {R}{x^aR}\to \frac {R}{x^bR}\to 0$
be a short exact sequence, where
$\sigma :0\to F_1\to F_2\oplus \frac {R}{x^aR}\to \frac {R}{x^bR}\to 0$
be a short exact sequence, where
![]() $a,b$
are nonnegative integers and
$a,b$
are nonnegative integers and
![]() $F_1,F_2$
are free R-modules. Let c be an integer such that
$F_1,F_2$
are free R-modules. Let c be an integer such that
![]() $c\ge b$
and
$c\ge b$
and
![]() $\sigma \otimes \frac {R}{x^cR}$
is short exact. Then
$\sigma \otimes \frac {R}{x^cR}$
is short exact. Then
![]() $a=b$
and
$a=b$
and
![]() $\operatorname{rank}(F_2)= \operatorname{rank}(F_1)$
. So, in particular,
$\operatorname{rank}(F_2)= \operatorname{rank}(F_1)$
. So, in particular,
![]() $\sigma $
is split exact.
$\sigma $
is split exact.
Proof. Since
![]() $x\in R$
is a nonzero divisor, so
$x\in R$
is a nonzero divisor, so
![]() $\frac {R}{x^aR}, \frac {R}{x^bR}$
are torsion modules, that is, have constant rank
$\frac {R}{x^aR}, \frac {R}{x^bR}$
are torsion modules, that is, have constant rank
![]() $0$
. Hence, calculating rank along
$0$
. Hence, calculating rank along
![]() $\sigma $
, we get
$\sigma $
, we get
![]() $\operatorname{rank}(F_2)= \operatorname{rank}(F_1)$
. Next, we will show that
$\operatorname{rank}(F_2)= \operatorname{rank}(F_1)$
. Next, we will show that
![]() $a\le b$
. Dualizing
$a\le b$
. Dualizing
![]() $\sigma $
by R, we get the following part of a long exact sequence:
$\sigma $
by R, we get the following part of a long exact sequence:
![]() ${\operatorname{Ext}}^1_R\left (\frac {R}{x^bR},R\right )\to {\operatorname{Ext}}^1_R\left (\frac {R}{x^aR},R\right )\to 0$
. Now, since
${\operatorname{Ext}}^1_R\left (\frac {R}{x^bR},R\right )\to {\operatorname{Ext}}^1_R\left (\frac {R}{x^aR},R\right )\to 0$
. Now, since
![]() $x^a\in R$
is a nonzero divisor, by taking the resolution
$x^a\in R$
is a nonzero divisor, by taking the resolution
![]() $0\to R\xrightarrow {\cdot x^a}R\to \frac {R}{x^aR}\to 0$
of
$0\to R\xrightarrow {\cdot x^a}R\to \frac {R}{x^aR}\to 0$
of
![]() $\frac {R}{x^aR}$
, and dualizing by R, and calculating the cohomology, we get that
$\frac {R}{x^aR}$
, and dualizing by R, and calculating the cohomology, we get that
![]() ${\operatorname{Ext}}^1_R\left (\frac {R}{x^aR},R\right )\cong \frac {R}{x^aR}$
. Similarly,
${\operatorname{Ext}}^1_R\left (\frac {R}{x^aR},R\right )\cong \frac {R}{x^aR}$
. Similarly,
![]() ${\operatorname{Ext}}^1_R\left (\frac {R}{x^bR},R\right )\cong \frac {R}{x^bR}$
. Hence, we have the exact sequence
${\operatorname{Ext}}^1_R\left (\frac {R}{x^bR},R\right )\cong \frac {R}{x^bR}$
. Hence, we have the exact sequence
![]() $\frac {R}{x^bR}\to \frac {R}{x^aR}\to 0$
. Since
$\frac {R}{x^bR}\to \frac {R}{x^aR}\to 0$
. Since
![]() $x^b$
annihilates
$x^b$
annihilates
![]() $\frac {R}{x^bR}$
, we have
$\frac {R}{x^bR}$
, we have
![]() $x^b$
annihilates
$x^b$
annihilates
![]() $\frac {R}{x^aR}$
as well, which implies
$\frac {R}{x^aR}$
as well, which implies
![]() $x^bR\subseteq x^aR$
. Since
$x^bR\subseteq x^aR$
. Since
![]() $x\in \mathfrak {m}$
is R-regular, so
$x\in \mathfrak {m}$
is R-regular, so
![]() $x^bR\subseteq x^aR$
implies that
$x^bR\subseteq x^aR$
implies that
![]() $a\leq b$
. Since
$a\leq b$
. Since
![]() $\sigma \otimes \frac {R}{x^cR}$
is short exact, we have the following short exact sequence:
$\sigma \otimes \frac {R}{x^cR}$
is short exact, we have the following short exact sequence:
 $$ \begin{align*}\sigma\otimes \frac{R}{x^cR}:0\to \left(\frac{R}{x^cR}\right)^{\oplus l_1}\to\left(\frac{R}{x^cR}\right)^{\oplus l_2}\oplus\frac{R}{x^aR}\to \frac{R}{x^bR}\to 0,\end{align*} $$
$$ \begin{align*}\sigma\otimes \frac{R}{x^cR}:0\to \left(\frac{R}{x^cR}\right)^{\oplus l_1}\to\left(\frac{R}{x^cR}\right)^{\oplus l_2}\oplus\frac{R}{x^aR}\to \frac{R}{x^bR}\to 0,\end{align*} $$
where we have used that
![]() $\frac {R}{x^cR}\otimes \frac {R}{x^aR}\cong \frac {R}{x^cR+x^aR}\cong \frac {R}{x^aR}$
and
$\frac {R}{x^cR}\otimes \frac {R}{x^aR}\cong \frac {R}{x^cR+x^aR}\cong \frac {R}{x^aR}$
and
![]() $\frac {R}{x^cR}\otimes \frac {R}{x^bR}\cong \frac {R}{x^cR+x^bR}\cong \frac {R}{x^bR}$
, as
$\frac {R}{x^cR}\otimes \frac {R}{x^bR}\cong \frac {R}{x^cR+x^bR}\cong \frac {R}{x^bR}$
, as
![]() $a\leq b\leq c$
. Since R is local Cohen–Macaulay of dimension
$a\leq b\leq c$
. Since R is local Cohen–Macaulay of dimension
![]() $1$
and
$1$
and
![]() $x\in \mathfrak {m}$
is R-regular, we have
$x\in \mathfrak {m}$
is R-regular, we have
![]() $x^aR, x^b R, x^c R$
are
$x^aR, x^b R, x^c R$
are
![]() $\mathfrak {m}$
-primary ideals. Hence, by calculating the length along the short exact sequence
$\mathfrak {m}$
-primary ideals. Hence, by calculating the length along the short exact sequence
![]() $\sigma \otimes \frac {R}{x^cR}$
, we get that
$\sigma \otimes \frac {R}{x^cR}$
, we get that
![]() $\lambda \left (\frac {R}{x^bR}\right )-\lambda \left (\frac {R}{x^aR}\right )=(l_2-l_1)\lambda \left (\frac {R}{x^cR}\right )=0$
. Since
$\lambda \left (\frac {R}{x^bR}\right )-\lambda \left (\frac {R}{x^aR}\right )=(l_2-l_1)\lambda \left (\frac {R}{x^cR}\right )=0$
. Since
![]() $x^bR\subseteq x^aR$
, so
$x^bR\subseteq x^aR$
, so
![]() $\lambda \left (\frac {R}{x^bR}\right )=\lambda \left (\frac {R}{x^aR}\right )$
now implies
$\lambda \left (\frac {R}{x^bR}\right )=\lambda \left (\frac {R}{x^aR}\right )$
now implies
![]() $x^aR=x^bR$
by calculating length along the short exact sequence
$x^aR=x^bR$
by calculating length along the short exact sequence
![]() $0\to \frac {x^aR}{x^bR}\to \frac {R}{x^bR}\to \frac {R}{x^aR}\to 0$
. Since
$0\to \frac {x^aR}{x^bR}\to \frac {R}{x^bR}\to \frac {R}{x^aR}\to 0$
. Since
![]() $x\in \mathfrak {m}$
is R-regular, we have
$x\in \mathfrak {m}$
is R-regular, we have
![]() $a=b$
. Finally, since
$a=b$
. Finally, since
![]() $F_1\cong F_2$
and
$F_1\cong F_2$
and
![]() $a=b$
, we get
$a=b$
, we get
![]() $\sigma $
is split exact.
$\sigma $
is split exact.
In the following,
![]() $\operatorname{H}^0_{\mathfrak {m}}(-)$
denotes the zeroth local cohomology module. For a finite length R-module M,
$\operatorname{H}^0_{\mathfrak {m}}(-)$
denotes the zeroth local cohomology module. For a finite length R-module M,
![]() $\ell \ell (M)$
will stand for the smallest integer
$\ell \ell (M)$
will stand for the smallest integer
![]() $n\ge 0$
such that
$n\ge 0$
such that
![]() $\mathfrak {m}^n M=0$
.
$\mathfrak {m}^n M=0$
.
Proposition 5.1.16. Let
![]() $(R,\mathfrak {m})$
be a regular local ring of dimension
$(R,\mathfrak {m})$
be a regular local ring of dimension
![]() $1$
. Let
$1$
. Let
![]() $L\in {\operatorname{mod}}(R)$
. Let c be an integer such that
$L\in {\operatorname{mod}}(R)$
. Let c be an integer such that
![]() $c\ge \ell \ell (\operatorname{H}^0_{\mathfrak {m}}(L))$
. Consider the function
$c\ge \ell \ell (\operatorname{H}^0_{\mathfrak {m}}(L))$
. Consider the function
![]() $\phi _L(-):=\lambda (\frac {R}{\mathfrak {m}^{c}}\otimes -):{\operatorname{mod}}(R)\to \mathbb {N}\cup \{0\}$
. Then, for any free R-module F, we have
$\phi _L(-):=\lambda (\frac {R}{\mathfrak {m}^{c}}\otimes -):{\operatorname{mod}}(R)\to \mathbb {N}\cup \{0\}$
. Then, for any free R-module F, we have
![]() ${\operatorname{Ext}}_R^1(L,F)^{\phi _L}=0$
.
${\operatorname{Ext}}_R^1(L,F)^{\phi _L}=0$
.
Proof. Note that R is not a field, since
![]() $\dim R=1$
. Since R is a regular local ring, we have
$\dim R=1$
. Since R is a regular local ring, we have
![]() $L\cong G\oplus L'$
, where G is a finite free R-module and
$L\cong G\oplus L'$
, where G is a finite free R-module and
![]() $L'$
is an R-module of finite length. We have
$L'$
is an R-module of finite length. We have
![]() $\operatorname{H}^0_{\mathfrak {m}}(L)\cong L'$
. Since
$\operatorname{H}^0_{\mathfrak {m}}(L)\cong L'$
. Since
![]() ${\operatorname{Ext}}^1_R(L,F)^{\phi _L}\cong {\operatorname{Ext}}^1_R(G,F)^{\phi _L}\oplus {\operatorname{Ext}}^1_R(L',F)^{\phi _L}\cong {\operatorname{Ext}}^1_R(L',F)^{\phi _L}$
, we may replace L by
${\operatorname{Ext}}^1_R(L,F)^{\phi _L}\cong {\operatorname{Ext}}^1_R(G,F)^{\phi _L}\oplus {\operatorname{Ext}}^1_R(L',F)^{\phi _L}\cong {\operatorname{Ext}}^1_R(L',F)^{\phi _L}$
, we may replace L by
![]() $L'$
, and assume without loss of generality that L has finite length, and
$L'$
, and assume without loss of generality that L has finite length, and
![]() $c\ge \ell \ell (L)$
. For simplicity, we denote
$c\ge \ell \ell (L)$
. For simplicity, we denote
![]() $\phi _L=\phi $
. Now, it is enough to show that
$\phi _L=\phi $
. Now, it is enough to show that
![]() ${\operatorname{Ext}}_R^1(L,R)^{\phi }=0$
. Since
${\operatorname{Ext}}_R^1(L,R)^{\phi }=0$
. Since
![]() $(R,\mathfrak {m})$
is a regular local ring of dimension
$(R,\mathfrak {m})$
is a regular local ring of dimension
![]() $1$
, R is a PID. Hence,
$1$
, R is a PID. Hence,
![]() $\mathfrak {m}=xR$
for some
$\mathfrak {m}=xR$
for some
![]() $x\neq 0$
. Since L is a finite length module, by the structure theorem of modules over a PID, we have
$x\neq 0$
. Since L is a finite length module, by the structure theorem of modules over a PID, we have
![]() $L\cong \oplus _{i=1}^{n} \frac {R}{x^{b_i}R}$
, where
$L\cong \oplus _{i=1}^{n} \frac {R}{x^{b_i}R}$
, where
![]() $b_i>0$
. So,
$b_i>0$
. So,
![]() $\ell \ell (L)=\max _{1\le i\le n}{b_i}$
. Hence, it is enough to show that
$\ell \ell (L)=\max _{1\le i\le n}{b_i}$
. Hence, it is enough to show that
![]() ${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }=0$
for all
${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }=0$
for all
![]() $i=1,\ldots ,n$
. Fix an
$i=1,\ldots ,n$
. Fix an
![]() $i\in \{1,\ldots ,n\}$
and consider a short exact sequence
$i\in \{1,\ldots ,n\}$
and consider a short exact sequence
![]() $\sigma :0\to R\to X\to \frac {R}{x^{b_i}R}\to 0$
in
$\sigma :0\to R\to X\to \frac {R}{x^{b_i}R}\to 0$
in
![]() ${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }$
. By the structure theorem of modules over a PID, we also have
${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }$
. By the structure theorem of modules over a PID, we also have
![]() $X\cong R^{\oplus s}\oplus \left (\oplus _{j=1}^t\frac {R}{x^{a_j}R}\right )$
, where
$X\cong R^{\oplus s}\oplus \left (\oplus _{j=1}^t\frac {R}{x^{a_j}R}\right )$
, where
![]() $a_j>0$
. As R is an integral domain and
$a_j>0$
. As R is an integral domain and
![]() $\frac {R}{x^{b_i}R}$
and
$\frac {R}{x^{b_i}R}$
and
![]() $\frac {R}{x^{a_j}R}$
are all torsion R-modules, so calculating rank along the short exact sequence
$\frac {R}{x^{a_j}R}$
are all torsion R-modules, so calculating rank along the short exact sequence
![]() $\sigma $
, we obtain
$\sigma $
, we obtain
![]() $s=1$
. Moreover,
$s=1$
. Moreover,
![]() $1+t=s+t=\mu (X)\leq 2$
, since
$1+t=s+t=\mu (X)\leq 2$
, since
![]() $\mu $
is subadditive. Thus,
$\mu $
is subadditive. Thus,
![]() $t\leq 1$
. If
$t\leq 1$
. If
![]() $t=0$
, then we obtain
$t=0$
, then we obtain
![]() $\sigma :0\to R\to R \oplus \frac {R}{x^0R}\to \frac {R}{x^{b_i}R}\to 0$
. Since
$\sigma :0\to R\to R \oplus \frac {R}{x^0R}\to \frac {R}{x^{b_i}R}\to 0$
. Since
![]() $\sigma $
is
$\sigma $
is
![]() $\phi $
-additive, by using Lemma 4.12 with the functor
$\phi $
-additive, by using Lemma 4.12 with the functor
![]() $\lambda _R\left (\frac {R}{\mathfrak {m}^{c}} \otimes _R -\right )$
, we obtain that
$\lambda _R\left (\frac {R}{\mathfrak {m}^{c}} \otimes _R -\right )$
, we obtain that
![]() $\sigma \otimes \frac {R}{\mathfrak {m}^{c}}=\sigma \otimes \frac {R}{x^{c}R}$
is short exact. As
$\sigma \otimes \frac {R}{\mathfrak {m}^{c}}=\sigma \otimes \frac {R}{x^{c}R}$
is short exact. As
![]() $c\geq b_i>0$
, we obtain a contradiction from Lemma 5.1.15. Thus,
$c\geq b_i>0$
, we obtain a contradiction from Lemma 5.1.15. Thus,
![]() $t=1$
. So, we get
$t=1$
. So, we get
![]() $X\cong R\oplus \frac {R}{x^{a}R}$
for some
$X\cong R\oplus \frac {R}{x^{a}R}$
for some
![]() $a=a_j$
. Thus, we have the short exact sequence
$a=a_j$
. Thus, we have the short exact sequence
![]() $\sigma :0\to R\to R\oplus \frac {R}{x^{a}R}\to \frac {R}{x^{b_i}R}\to 0$
.
$\sigma :0\to R\to R\oplus \frac {R}{x^{a}R}\to \frac {R}{x^{b_i}R}\to 0$
.
Since
![]() $c\ge \ell \ell (L)=\max _{1\le i\le n}{b_i}$
, we have
$c\ge \ell \ell (L)=\max _{1\le i\le n}{b_i}$
, we have
![]() $c\ge b_i$
for all
$c\ge b_i$
for all
![]() $i=1,\ldots ,n$
. Hence, by applying Lemma 5.1.15 on
$i=1,\ldots ,n$
. Hence, by applying Lemma 5.1.15 on
![]() $\sigma $
, we get that
$\sigma $
, we get that
![]() $\sigma $
is split exact. Since
$\sigma $
is split exact. Since
![]() $\sigma $
is an arbitrary element of
$\sigma $
is an arbitrary element of
![]() ${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }$
, we get
${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }$
, we get
![]() ${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }=0$
for all
${\operatorname{Ext}}_R^1\left (\frac {R}{x^{b_i}R},R\right )^{\phi }=0$
for all
![]() $i=1,\ldots ,n$
. This implies that
$i=1,\ldots ,n$
. This implies that
![]() ${\operatorname{Ext}}_R^1\left (L,R\right )^{\phi }=0$
, so
${\operatorname{Ext}}_R^1\left (L,R\right )^{\phi }=0$
, so
![]() ${\operatorname{Ext}}_R^1\left (L,F\right )^{\phi }=0$
.
${\operatorname{Ext}}_R^1\left (L,F\right )^{\phi }=0$
.
Taking
![]() $L=k$
and
$L=k$
and
![]() $c=1=\ell \ell (k)$
, we see that
$c=1=\ell \ell (k)$
, we see that
![]() $\phi _L(-)=\mu (-)$
in Proposition 5.1.16. So, we also get another proof of Corollary 5.1.4 in dimension
$\phi _L(-)=\mu (-)$
in Proposition 5.1.16. So, we also get another proof of Corollary 5.1.4 in dimension
![]() $1$
.
$1$
.
Next, we compare
![]() ${\operatorname{Ext}}^1_R(M,R)^{\mu }$
with
${\operatorname{Ext}}^1_R(M,R)^{\mu }$
with
![]() ${\operatorname{Ext}}^1_R(M,R)$
. In arbitrary dimension, we only consider this for local Cohen–Macaulay rings of minimal multiplicity. We first record some general preliminary lemmas.
${\operatorname{Ext}}^1_R(M,R)$
. In arbitrary dimension, we only consider this for local Cohen–Macaulay rings of minimal multiplicity. We first record some general preliminary lemmas.
Lemma 5.1.17. Let
![]() $(R,\mathfrak {m},k)$
be a local ring such that
$(R,\mathfrak {m},k)$
be a local ring such that
![]() $\mathfrak {m}^2=0$
and
$\mathfrak {m}^2=0$
and
![]() $\mathfrak {m}\neq 0$
. Let
$\mathfrak {m}\neq 0$
. Let
![]() $e:=\mu (\mathfrak {m})$
. Then
$e:=\mu (\mathfrak {m})$
. Then
![]() $\mu (\omega _R)=e$
,
$\mu (\omega _R)=e$
,
![]() $\mu (\Omega _R\omega _R)=e^2-1$
, and
$\mu (\Omega _R\omega _R)=e^2-1$
, and
![]() $\Omega _R\omega _R\cong k^{\oplus (e^2-1)}$
.
$\Omega _R\omega _R\cong k^{\oplus (e^2-1)}$
.
Proof. Since
![]() $\mathfrak {m}^2=0$
and
$\mathfrak {m}^2=0$
and
![]() $\mathfrak {m}\neq 0$
, we have
$\mathfrak {m}\neq 0$
, we have
![]() $\mathfrak {m}\subseteq (0:_R\mathfrak {m})\subsetneq R$
. Hence,
$\mathfrak {m}\subseteq (0:_R\mathfrak {m})\subsetneq R$
. Hence,
![]() $\mathfrak {m}=(0:_R\mathfrak {m})$
. Then we have
$\mathfrak {m}=(0:_R\mathfrak {m})$
. Then we have
![]() ${\mu }({\omega }_R)={\operatorname{r}}(R)=\dim _k(0:_R\mathfrak {m})=\dim _k\mathfrak {m}=\dim _k\left (\frac {\mathfrak {m}}{\mathfrak {m}^2}\right )=\mu (\mathfrak {m})=e$
. Also, note that
${\mu }({\omega }_R)={\operatorname{r}}(R)=\dim _k(0:_R\mathfrak {m})=\dim _k\mathfrak {m}=\dim _k\left (\frac {\mathfrak {m}}{\mathfrak {m}^2}\right )=\mu (\mathfrak {m})=e$
. Also, note that
![]() $\lambda (R)=\lambda \left (\frac {R}{\mathfrak {m}^2}\right )=\lambda \left (\frac {R}{\mathfrak {m}}\right )+\lambda \left (\frac {\mathfrak {m}}{\mathfrak {m}^2}\right )=1+\mu (\mathfrak {m})$
. Next, consider the short exact sequence
$\lambda (R)=\lambda \left (\frac {R}{\mathfrak {m}^2}\right )=\lambda \left (\frac {R}{\mathfrak {m}}\right )+\lambda \left (\frac {\mathfrak {m}}{\mathfrak {m}^2}\right )=1+\mu (\mathfrak {m})$
. Next, consider the short exact sequence
![]() $0\to \Omega _R\omega _R\to R^{\oplus \mu (\omega _R)}\to \omega _R\to 0$
, so
$0\to \Omega _R\omega _R\to R^{\oplus \mu (\omega _R)}\to \omega _R\to 0$
, so
![]() $\Omega _R\omega _R\subseteq \mathfrak {m} R^{\oplus \mu (\omega _R)}$
. Hence,
$\Omega _R\omega _R\subseteq \mathfrak {m} R^{\oplus \mu (\omega _R)}$
. Hence,
![]() $\mathfrak {m}\Omega _R\omega _R=0$
. This implies that
$\mathfrak {m}\Omega _R\omega _R=0$
. This implies that
 $\mu (\Omega _R\omega _R)=\lambda \left (\frac {\Omega _R\omega _R}{\mathfrak {m}\Omega _R\omega _R}\right )=\lambda (\Omega _R\omega _R)=\lambda (R^{\oplus \mu (\omega _R)})-\lambda (\omega _R)=\mu (\omega _R)\lambda (R)-\lambda (R)=\lambda (R)(\mu (\omega _R)-1)=\lambda (R)(\mu (\mathfrak {m})-1)=(1+\mu (\mathfrak {m}))(\mu (\mathfrak {m})-1)=e^2-1$
, where
$\mu (\Omega _R\omega _R)=\lambda \left (\frac {\Omega _R\omega _R}{\mathfrak {m}\Omega _R\omega _R}\right )=\lambda (\Omega _R\omega _R)=\lambda (R^{\oplus \mu (\omega _R)})-\lambda (\omega _R)=\mu (\omega _R)\lambda (R)-\lambda (R)=\lambda (R)(\mu (\omega _R)-1)=\lambda (R)(\mu (\mathfrak {m})-1)=(1+\mu (\mathfrak {m}))(\mu (\mathfrak {m})-1)=e^2-1$
, where
![]() $\lambda (\omega _R)=\lambda (R)$
follows from Matlis duality.
$\lambda (\omega _R)=\lambda (R)$
follows from Matlis duality.
Lemma 5.1.18. Let
![]() $(R,\mathfrak {m},k)$
be a local ring, and let M be a finitely generated R-module. If x is M-regular, then
$(R,\mathfrak {m},k)$
be a local ring, and let M be a finitely generated R-module. If x is M-regular, then
![]() $\frac {\Omega _R M}{x\Omega _R M}\cong \Omega _{R/xR}\left (\frac {M}{xM}\right )$
.
$\frac {\Omega _R M}{x\Omega _R M}\cong \Omega _{R/xR}\left (\frac {M}{xM}\right )$
.
Proof. Since x is M-regular, we have
![]() $\operatorname{Tor}_1^R(M,\frac {R}{xR})=0$
. Hence, tensoring the short exact sequence
$\operatorname{Tor}_1^R(M,\frac {R}{xR})=0$
. Hence, tensoring the short exact sequence
![]() $0\to \Omega _R M\to R^{\oplus \mu _R(M)}\to M\to 0$
with
$0\to \Omega _R M\to R^{\oplus \mu _R(M)}\to M\to 0$
with
![]() $R/xR$
, we get the exact sequence
$R/xR$
, we get the exact sequence
![]() $0\to \frac {\Omega _R M}{x\Omega _R M}\to (\frac {R}{xR})^{\oplus \mu _R(M)}\to \frac {M}{xM}\to 0$
. Since
$0\to \frac {\Omega _R M}{x\Omega _R M}\to (\frac {R}{xR})^{\oplus \mu _R(M)}\to \frac {M}{xM}\to 0$
. Since
![]() $\mu _R(M)=\mu _{\frac {R}{xR}}(\frac {M}{xM})$
, we have
$\mu _R(M)=\mu _{\frac {R}{xR}}(\frac {M}{xM})$
, we have
![]() $\frac {\Omega _R M}{x\Omega _R M}\cong \Omega _{R/xR}\left (\frac {M}{xM}\right )$
.
$\frac {\Omega _R M}{x\Omega _R M}\cong \Omega _{R/xR}\left (\frac {M}{xM}\right )$
.
5.1.19. Since
 $\mu _R(-)=\lambda _R\left (\dfrac {(-)}{\mathfrak {m}(-)}\right )$
, it follows by 4.3 that
$\mu _R(-)=\lambda _R\left (\dfrac {(-)}{\mathfrak {m}(-)}\right )$
, it follows by 4.3 that
![]() $\mu _R((-))=\mu _S(S\otimes _R(-))$
, where
$\mu _R((-))=\mu _S(S\otimes _R(-))$
, where
![]() $S=R[X]_{\mathfrak {m}[X]}$
. Since tensoring with S preserves exactness, so tensoring a minimal free resolution
$S=R[X]_{\mathfrak {m}[X]}$
. Since tensoring with S preserves exactness, so tensoring a minimal free resolution
![]() $(F_{\bullet },\partial _{\bullet })$
of an R-module M with S and remembering
$(F_{\bullet },\partial _{\bullet })$
of an R-module M with S and remembering
![]() $S\otimes \partial $
now have entries in
$S\otimes \partial $
now have entries in
![]() $\mathfrak {m} S$
, the maximal ideal of S, we see that
$\mathfrak {m} S$
, the maximal ideal of S, we see that
![]() $S\otimes _R \Omega _R M\cong \Omega _S(S\otimes _S M)$
. Also, if
$S\otimes _R \Omega _R M\cong \Omega _S(S\otimes _S M)$
. Also, if
![]() $\omega _R$
exists, then owing to the fact that
$\omega _R$
exists, then owing to the fact that
![]() $S/\mathfrak {m} S$
is a field, we see that
$S/\mathfrak {m} S$
is a field, we see that
![]() $\omega _S$
also exists and
$\omega _S$
also exists and
![]() $\omega _S\cong S\otimes _R \omega _R$
by [Reference Bruns and Herzog3, Th. 3.3.14(a)]. Hence,
$\omega _S\cong S\otimes _R \omega _R$
by [Reference Bruns and Herzog3, Th. 3.3.14(a)]. Hence,
![]() $S\otimes _R \operatorname{Hom}_R(-,\omega _R)\cong \operatorname{Hom}_S\left (S\otimes _R(-),\omega _S\right )$
. Finally, we also have
$S\otimes _R \operatorname{Hom}_R(-,\omega _R)\cong \operatorname{Hom}_S\left (S\otimes _R(-),\omega _S\right )$
. Finally, we also have
![]() ${\operatorname{r}}(R)={\operatorname{r}}(S)$
by [Reference Bruns and Herzog3, Prop. 1.2.16(b)].
${\operatorname{r}}(R)={\operatorname{r}}(S)$
by [Reference Bruns and Herzog3, Prop. 1.2.16(b)].
Proposition 5.1.20. Let
![]() $(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of minimal multiplicity admitting a canonical module
$(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of minimal multiplicity admitting a canonical module
![]() $\omega _R$
, and let
$\omega _R$
, and let
![]() $\mathfrak {m}\neq 0$
. Then
$\mathfrak {m}\neq 0$
. Then
![]() $\mu ((\Omega _R\omega _R)^{\dagger })={\operatorname{r}}(R)^2-1$
.
$\mu ((\Omega _R\omega _R)^{\dagger })={\operatorname{r}}(R)^2-1$
.
Proof. Due to 5.1.19, we may pass to the faithfully flat extension
![]() $S:=R[X]_{\mathfrak {m}[X]}$
and assume that the residue field is infinite.
$S:=R[X]_{\mathfrak {m}[X]}$
and assume that the residue field is infinite.
We will prove the claim by induction on
![]() $\dim R=d$
. First, let
$\dim R=d$
. First, let
![]() $d=0$
. Since R has minimal multiplicity, we have
$d=0$
. Since R has minimal multiplicity, we have
![]() $\mathfrak {m}^2=0$
. Hence, by Lemma 5.1.17, we get that
$\mathfrak {m}^2=0$
. Hence, by Lemma 5.1.17, we get that
![]() $\Omega _R\omega _R\cong k^{\oplus ({\operatorname{r}}(R)^2-1)}$
. This implies
$\Omega _R\omega _R\cong k^{\oplus ({\operatorname{r}}(R)^2-1)}$
. This implies
![]() $(\Omega _R\omega _R)^{\dagger }\cong k^{\oplus ({\operatorname{r}}(R)^2-1)}$
, so
$(\Omega _R\omega _R)^{\dagger }\cong k^{\oplus ({\operatorname{r}}(R)^2-1)}$
, so
![]() $\mu ((\Omega _R\omega _R)^{\dagger })={\operatorname{r}}(R)^2-1$
. Now, let
$\mu ((\Omega _R\omega _R)^{\dagger })={\operatorname{r}}(R)^2-1$
. Now, let
![]() $\dim R=d\ge 1$
, and let the claim be true for rings with dimension
$\dim R=d\ge 1$
, and let the claim be true for rings with dimension
![]() $d-1$
. Let
$d-1$
. Let
![]() $x\in \mathfrak {m}$
be such that
$x\in \mathfrak {m}$
be such that
![]() $\mathfrak {m}^2=(x,x_1,...,x_{d-1})\mathfrak {m}$
(see [Reference Bruns and Herzog3, Exer. 4.6.14(c)]). So,
$\mathfrak {m}^2=(x,x_1,...,x_{d-1})\mathfrak {m}$
(see [Reference Bruns and Herzog3, Exer. 4.6.14(c)]). So,
![]() $\frac {R}{xR}$
has minimal multiplicity. Now, we have
$\frac {R}{xR}$
has minimal multiplicity. Now, we have
 $$ \begin{align*} \frac{(\Omega_R\omega_R)^{\dagger}}{x(\Omega_R\omega_R)^{\dagger}} &\cong\left(\frac{\Omega_R\omega_R}{x\Omega_R\omega_R}\right)^{\dagger}\cong \left(\Omega_{\frac{R}{xR}}\left(\frac{\omega_R}{x\omega_R}\right)\right)^{\dagger}\cong \left(\Omega_{\frac{R}{xR}}\omega_{\frac{R}{xR}}\right)^{\dagger}, \end{align*} $$
$$ \begin{align*} \frac{(\Omega_R\omega_R)^{\dagger}}{x(\Omega_R\omega_R)^{\dagger}} &\cong\left(\frac{\Omega_R\omega_R}{x\Omega_R\omega_R}\right)^{\dagger}\cong \left(\Omega_{\frac{R}{xR}}\left(\frac{\omega_R}{x\omega_R}\right)\right)^{\dagger}\cong \left(\Omega_{\frac{R}{xR}}\omega_{\frac{R}{xR}}\right)^{\dagger}, \end{align*} $$
where the first isomorphism follows from [Reference Bruns and Herzog3, Prop. 3.3.3(a)], and the second isomorphism is by Lemma 5.1.18. So,
 $$ \begin{align*} \mu_R((\Omega_R\omega_R)^{\dagger}) =\mu_{\frac{R}{xR}}\left(\frac{(\Omega_R\omega_R)^{\dagger}}{x(\Omega_R\omega_R)^{\dagger}}\right)&=\mu_{\frac{R}{xR}}\left(\left(\Omega_{\frac{R}{xR}}\omega_{\frac{R}{xR}}\right)^{\dagger}\right)\\ &=r\left(\frac{R}{xR}\right)^2-1\text{ [By induction hypothesis]}\\ &={\operatorname{r}}(R)^2-1.\\[-45pt] \end{align*} $$
$$ \begin{align*} \mu_R((\Omega_R\omega_R)^{\dagger}) =\mu_{\frac{R}{xR}}\left(\frac{(\Omega_R\omega_R)^{\dagger}}{x(\Omega_R\omega_R)^{\dagger}}\right)&=\mu_{\frac{R}{xR}}\left(\left(\Omega_{\frac{R}{xR}}\omega_{\frac{R}{xR}}\right)^{\dagger}\right)\\ &=r\left(\frac{R}{xR}\right)^2-1\text{ [By induction hypothesis]}\\ &={\operatorname{r}}(R)^2-1.\\[-45pt] \end{align*} $$
Proposition 5.1.21. Let
![]() $(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of minimal multiplicity admitting a canonical module
$(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of minimal multiplicity admitting a canonical module
![]() $\omega _R$
. Then the exact sequence
$\omega _R$
. Then the exact sequence
![]() $0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
is
$0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
is
![]() $\mu $
-additive.
$\mu $
-additive.
Proof. Consider the exact sequence
![]() $0\to \Omega _R\omega _R\to R^{\oplus \mu (\omega _R)}\to \omega _R\to 0$
. Since
$0\to \Omega _R\omega _R\to R^{\oplus \mu (\omega _R)}\to \omega _R\to 0$
. Since
![]() ${\operatorname{Ext}}^1_R(\omega _R,\omega _R)=0$
, we have the exact sequence
${\operatorname{Ext}}^1_R(\omega _R,\omega _R)=0$
, we have the exact sequence
![]() $0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
. From Proposition 5.1.20, we have
$0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
. From Proposition 5.1.20, we have
![]() $\mu ((\Omega _R\omega _R)^{\dagger })={\operatorname{r}}(R)^2-1=\mu (\omega _R)^2-\mu (R)=\mu (\omega _R^{\oplus \mu (\omega _R)})-\mu (R)$
. Hence,
$\mu ((\Omega _R\omega _R)^{\dagger })={\operatorname{r}}(R)^2-1=\mu (\omega _R)^2-\mu (R)=\mu (\omega _R^{\oplus \mu (\omega _R)})-\mu (R)$
. Hence,
![]() $0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
is
$0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
is
![]() $\mu $
-additive.
$\mu $
-additive.
Proposition 5.1.22. Let
![]() $(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of minimal multiplicity. Then
$(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of minimal multiplicity. Then
![]() ${\operatorname{Ext}}^1_R(M,F)={\operatorname{Ext}}^1_R(M,F)^{\mu }$
for any maximal Cohen–Macaulay R-module M and any finitely generated free R-module F.
${\operatorname{Ext}}^1_R(M,F)={\operatorname{Ext}}^1_R(M,F)^{\mu }$
for any maximal Cohen–Macaulay R-module M and any finitely generated free R-module F.
Proof. By Lemma 2.4, it is enough to prove the claim for
![]() $F=R$
.
$F=R$
.
We first consider the case when R has a canonical module
![]() $\omega _R$
. Consider the
$\omega _R$
. Consider the
![]() $\mu $
-additive (by Proposition 5.1.21) exact sequence
$\mu $
-additive (by Proposition 5.1.21) exact sequence
![]() $\sigma :0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
. Applying
$\sigma :0\to R\to \omega _R^{\oplus \mu (\omega _R)}\to (\Omega _R\omega _R)^{\dagger }\to 0$
. Applying
![]() $\operatorname{Hom}_R(M,-)$
to
$\operatorname{Hom}_R(M,-)$
to
![]() $\sigma $
, we get the following part of a commutative diagram of exact sequences by Corollary 3.9:
$\sigma $
, we get the following part of a commutative diagram of exact sequences by Corollary 3.9:

Since
![]() $\omega _R$
has finite injective dimension, we have
$\omega _R$
has finite injective dimension, we have
![]() ${\operatorname{Ext}}_{R}^1(M,\omega _R^{\oplus \mu (\omega _R)})=0$
by [Reference Bruns and Herzog3, Exer. 3.1.24]. So,
${\operatorname{Ext}}_{R}^1(M,\omega _R^{\oplus \mu (\omega _R)})=0$
by [Reference Bruns and Herzog3, Exer. 3.1.24]. So,
![]() ${\operatorname{Ext}}_{R}^1(M,\omega _R^{\oplus \mu (\omega _R)})^{\mu }=0$
as well. Hence, we get the following commutative diagram:
${\operatorname{Ext}}_{R}^1(M,\omega _R^{\oplus \mu (\omega _R)})^{\mu }=0$
as well. Hence, we get the following commutative diagram:

Thus,
![]() $h\circ g=f$
is surjective, so h is surjective. Since h is the natural inclusion map, we have
$h\circ g=f$
is surjective, so h is surjective. Since h is the natural inclusion map, we have
![]() ${\operatorname{Ext}}^1_R(M,R)={\operatorname{Ext}}^1_R(M,R)^{\mu }$
.
${\operatorname{Ext}}^1_R(M,R)={\operatorname{Ext}}^1_R(M,R)^{\mu }$
.
Now, we consider the general case. Since
![]() ${\operatorname{Ext}}^1_R(M,R)^{\mu }\subseteq {\operatorname{Ext}}_{R}^1(M,R)$
, it is enough to prove the other inclusion. So, let
${\operatorname{Ext}}^1_R(M,R)^{\mu }\subseteq {\operatorname{Ext}}_{R}^1(M,R)$
, it is enough to prove the other inclusion. So, let
![]() $\sigma : 0\to R\to X\to M\to 0 $
be an exact sequence. We need to show
$\sigma : 0\to R\to X\to M\to 0 $
be an exact sequence. We need to show
![]() $\sigma $
is
$\sigma $
is
![]() $\mu $
-additive. Now, consider the completion
$\mu $
-additive. Now, consider the completion
![]() $\widehat \sigma : 0\to \widehat R\to \widehat X\to \widehat M \to 0$
. Since
$\widehat \sigma : 0\to \widehat R\to \widehat X\to \widehat M \to 0$
. Since
![]() $\widehat R$
is Cohen–Macaulay, having minimal multiplicity, admitting a canonical module, and
$\widehat R$
is Cohen–Macaulay, having minimal multiplicity, admitting a canonical module, and
![]() $\widehat M$
is maximal Cohen–Macaulay over
$\widehat M$
is maximal Cohen–Macaulay over
![]() $\widehat R$
, by the first part of the proof, we get
$\widehat R$
, by the first part of the proof, we get
![]() $ {\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)={\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)^{\mu }$
. Thus,
$ {\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)={\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)^{\mu }$
. Thus,
![]() $[\widehat \sigma ]\in {\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)={\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)^{\mu }$
. Hence,
$[\widehat \sigma ]\in {\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)={\operatorname{Ext}}^1_{\widehat R}(\widehat M,\widehat R)^{\mu }$
. Hence,
![]() $\widehat \sigma $
is
$\widehat \sigma $
is
![]() $\mu $
-additive. Since the number of generators does not change under completion, we get
$\mu $
-additive. Since the number of generators does not change under completion, we get
![]() $\sigma $
is
$\sigma $
is
![]() $\mu $
-additive, which is what we wanted to prove.
$\mu $
-additive, which is what we wanted to prove.
Corollary 5.1.23. Let
![]() $(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of dimension d and minimal multiplicity. If
$(R,\mathfrak {m},k)$
be a local Cohen–Macaulay ring of dimension d and minimal multiplicity. If
![]() ${\operatorname{Ext}}^1_R(\Omega ^{i+d}_R k,R)^{\mu }=0$
for some
${\operatorname{Ext}}^1_R(\Omega ^{i+d}_R k,R)^{\mu }=0$
for some
![]() $i\geq 0$
, then R is a hypersurface.
$i\geq 0$
, then R is a hypersurface.
Proof. By Proposition 5.1.22, we have
![]() ${\operatorname{Ext}}^{d+i+1}_R(k,R)\cong {\operatorname{Ext}}^1_R(\Omega ^{d+i}_R k, R)={\operatorname{Ext}}^1_R(\Omega ^{d+i}_R k, R)^{\mu }=0$
. Hence, R has finite injective dimension by [Reference Roberts32, II, Th. 2], so R is Gorenstein. Since R has minimal multiplicity, R is a hypersurface.
${\operatorname{Ext}}^{d+i+1}_R(k,R)\cong {\operatorname{Ext}}^1_R(\Omega ^{d+i}_R k, R)={\operatorname{Ext}}^1_R(\Omega ^{d+i}_R k, R)^{\mu }=0$
. Hence, R has finite injective dimension by [Reference Roberts32, II, Th. 2], so R is Gorenstein. Since R has minimal multiplicity, R is a hypersurface.
One can also detect when a local ring has depth
![]() $0$
by comparing
$0$
by comparing
![]() ${\operatorname{Ext}}^1_R(M,R)$
to
${\operatorname{Ext}}^1_R(M,R)$
to
![]() ${\operatorname{Ext}}^1_R(M,R)^{\mu }$
as shown in the following proposition. In the following,
${\operatorname{Ext}}^1_R(M,R)^{\mu }$
as shown in the following proposition. In the following,
![]() $\operatorname{Tr}(-)$
stands for Auslander transpose (see [Reference Leuschke and Wiegand27, Def. 12.3]).
$\operatorname{Tr}(-)$
stands for Auslander transpose (see [Reference Leuschke and Wiegand27, Def. 12.3]).
Proposition 5.1.24. Let I be an ideal of a local ring
![]() $(R,\mathfrak {m},k)$
. Then,
$(R,\mathfrak {m},k)$
. Then,
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))$
. Moreover, the following are equivalent:
${\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))$
. Moreover, the following are equivalent:
-
(1)
 $\operatorname{depth} R=0$
.
$\operatorname{depth} R=0$
. -
(2)
 ${\operatorname{Ext}}^1_R(M,F)^{\mu }={\operatorname{Ext}}^1_R(M,F)$
for all finitely generated R-modules M and F, where F is free.
${\operatorname{Ext}}^1_R(M,F)^{\mu }={\operatorname{Ext}}^1_R(M,F)$
for all finitely generated R-modules M and F, where F is free. -
(3)
 ${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)^{\mu }= {\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
.
${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)^{\mu }= {\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
.
Proof. Since everywhere in this proposition the Auslander transpose is in the first component of
![]() ${\operatorname{Ext}}^1$
, our claim does not depend on the choice of
${\operatorname{Ext}}^1$
, our claim does not depend on the choice of
![]() $\operatorname{Tr}$
. First, we prove
$\operatorname{Tr}$
. First, we prove
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))$
. We may assume
${\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))$
. We may assume
![]() $\operatorname{Tr}(R/I)$
is non-free. Dualizing the exact sequence
$\operatorname{Tr}(R/I)$
is non-free. Dualizing the exact sequence
![]() $R^{\oplus \mu (I)} \to R \xrightarrow {\pi } R/I \to 0$
by R, we get
$R^{\oplus \mu (I)} \to R \xrightarrow {\pi } R/I \to 0$
by R, we get
![]() $0\to \operatorname{Hom}_R(R/I,R)\xrightarrow {\pi ^*} R\to R^{\oplus \mu (I)}\to \operatorname{Tr}(R/I)\to 0$
. Under the natural identification
$0\to \operatorname{Hom}_R(R/I,R)\xrightarrow {\pi ^*} R\to R^{\oplus \mu (I)}\to \operatorname{Tr}(R/I)\to 0$
. Under the natural identification
![]() $\operatorname{Hom}_R(R/I,R)\cong \operatorname{ann}_R(I)$
, the map
$\operatorname{Hom}_R(R/I,R)\cong \operatorname{ann}_R(I)$
, the map
![]() $\operatorname{Hom}_R(R/I,R)\xrightarrow {\pi ^*} R$
can be identified with the inclusion map
$\operatorname{Hom}_R(R/I,R)\xrightarrow {\pi ^*} R$
can be identified with the inclusion map
![]() $\operatorname{ann}_R(I)\to R$
, giving us
$\operatorname{ann}_R(I)\to R$
, giving us
![]() $0\to \operatorname{ann}_R(I) \to R \to R^{\oplus \mu (I)}\to \operatorname{Tr}(R/I)\to 0$
. Hence, we get an exact sequence
$0\to \operatorname{ann}_R(I) \to R \to R^{\oplus \mu (I)}\to \operatorname{Tr}(R/I)\to 0$
. Hence, we get an exact sequence
![]() $0\to R/\operatorname{ann}_R(I) \to R^{\oplus \mu (I)}\to \operatorname{Tr}(R/I)\to 0$
. Since
$0\to R/\operatorname{ann}_R(I) \to R^{\oplus \mu (I)}\to \operatorname{Tr}(R/I)\to 0$
. Since
![]() $\operatorname{Tr}(R/I)$
is non-free, this sequence gives us
$\operatorname{Tr}(R/I)$
is non-free, this sequence gives us
![]() $\Omega _R \operatorname{Tr}(R/I)\cong R/\operatorname{ann}_R(I)$
and the first Betti number of
$\Omega _R \operatorname{Tr}(R/I)\cong R/\operatorname{ann}_R(I)$
and the first Betti number of
![]() $\operatorname{Tr}(R/I)$
is
$\operatorname{Tr}(R/I)$
is
![]() $1$
. Hence,
$1$
. Hence,
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))$
by Lemma 5.1.3.
${\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr}(R/I),R/\operatorname{ann}_R(I))$
by Lemma 5.1.3.
Now, we prove the equivalence of the three conditions as follows:
![]() $(1) \implies (2)$
: Let
$(1) \implies (2)$
: Let
![]() $\sigma : 0\to F\to X\to M\to 0$
be an exact sequence, where F is a finitely generated free R-module. Since
$\sigma : 0\to F\to X\to M\to 0$
be an exact sequence, where F is a finitely generated free R-module. Since
![]() $\operatorname{depth} R=0$
, we get that k embeds inside R, that is, k is torsionless. Hence,
$\operatorname{depth} R=0$
, we get that k embeds inside R, that is, k is torsionless. Hence,
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr} k, R)=0$
by [Reference Leuschke and Wiegand27, Prop. 12.5]. Hence,
${\operatorname{Ext}}^1_R(\operatorname{Tr} k, R)=0$
by [Reference Leuschke and Wiegand27, Prop. 12.5]. Hence,
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr} k, F)=0$
. So, we get an exact sequence
${\operatorname{Ext}}^1_R(\operatorname{Tr} k, F)=0$
. So, we get an exact sequence
![]() $0\to \operatorname{Hom}_R(\operatorname{Tr} k,F)\to \operatorname{Hom}_R(\operatorname{Tr} k, X) \to \operatorname{Hom}_R(\operatorname{Tr} k, M)\to 0$
. Then, by [Reference Leuschke and Wiegand27, Exer. 13.36], we get that the sequence
$0\to \operatorname{Hom}_R(\operatorname{Tr} k,F)\to \operatorname{Hom}_R(\operatorname{Tr} k, X) \to \operatorname{Hom}_R(\operatorname{Tr} k, M)\to 0$
. Then, by [Reference Leuschke and Wiegand27, Exer. 13.36], we get that the sequence
![]() $0\to F \otimes _R k \to X \otimes _R k \to M \otimes _R k \to 0$
is also exact, which means
$0\to F \otimes _R k \to X \otimes _R k \to M \otimes _R k \to 0$
is also exact, which means
![]() $\sigma $
is
$\sigma $
is
![]() $\mu $
-additive. Thus,
$\mu $
-additive. Thus,
![]() ${\operatorname{Ext}}^1_R(M,F)^{\mu }={\operatorname{Ext}}^1_R(M,F)$
.
${\operatorname{Ext}}^1_R(M,F)^{\mu }={\operatorname{Ext}}^1_R(M,F)$
.
![]() $(2) \implies (3)$
Obvious.
$(2) \implies (3)$
Obvious.
![]() $(3) \implies (1)$
: Assume
$(3) \implies (1)$
: Assume
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)^{\mu }={\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
. Now, if possible let
${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)^{\mu }={\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
. Now, if possible let
![]() $\operatorname{depth} R>0$
. Then
$\operatorname{depth} R>0$
. Then
![]() $\mathfrak {m}$
contains a nonzero divisor, so
$\mathfrak {m}$
contains a nonzero divisor, so
![]() $\operatorname{ann}_R(\mathfrak {m})=0$
. Then, by the first part of this proposition, we get
$\operatorname{ann}_R(\mathfrak {m})=0$
. Then, by the first part of this proposition, we get
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
. Hence,
${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)^{\mu }=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
. Hence,
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
. Then, by Nakayama’s lemma,
${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)=\mathfrak {m} {\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)$
. Then, by Nakayama’s lemma,
![]() ${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)=0$
. Hence, by [Reference Leuschke and Wiegand27, Prop. 12.5], we have an embedding
${\operatorname{Ext}}^1_R(\operatorname{Tr} k,R)=0$
. Hence, by [Reference Leuschke and Wiegand27, Prop. 12.5], we have an embedding
![]() $k \to k^{**}$
. Consequently,
$k \to k^{**}$
. Consequently,
![]() $k^*\ne 0$
, that is,
$k^*\ne 0$
, that is,
![]() $\operatorname{depth} R=0$
.
$\operatorname{depth} R=0$
.
For general local Cohen–Macaulay rings of dimension
![]() $1$
, we now show that if
$1$
, we now show that if
![]() ${\operatorname{Ext}}^1_R(M,R)^{\mu }=0$
for some I-Ulrich module [Reference Dao, Maitra and Sridhar11, Def. 4.1]
${\operatorname{Ext}}^1_R(M,R)^{\mu }=0$
for some I-Ulrich module [Reference Dao, Maitra and Sridhar11, Def. 4.1]
![]() $M\subseteq Q(R)$
containing a nonzero divisor of R, then I is principal. For this, we first need the following lemma. For the remainder of this section, given R-submodules
$M\subseteq Q(R)$
containing a nonzero divisor of R, then I is principal. For this, we first need the following lemma. For the remainder of this section, given R-submodules
![]() $M,N$
of
$M,N$
of
![]() $Q(R)$
, by
$Q(R)$
, by
![]() $(M:N)$
, we will mean
$(M:N)$
, we will mean
![]() $\{x\in Q(R): xN\subseteq M\}$
.
$\{x\in Q(R): xN\subseteq M\}$
.
Lemma 5.1.25. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let I be an
$1$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal of R admitting a principal reduction
$\mathfrak {m}$
-primary ideal of R admitting a principal reduction
![]() $a\in I$
. Assume
$a\in I$
. Assume
![]() $(I:I)=R$
. If
$(I:I)=R$
. If
![]() $M\subseteq Q(R)$
is an I-Ulrich module, and contains a nonzero divisor of R, then the natural inclusion map
$M\subseteq Q(R)$
is an I-Ulrich module, and contains a nonzero divisor of R, then the natural inclusion map
![]() $\operatorname{Hom}_R\left (M,(a)\right )\to \operatorname{Hom}_R(M,I)$
, induced by the inclusion
$\operatorname{Hom}_R\left (M,(a)\right )\to \operatorname{Hom}_R(M,I)$
, induced by the inclusion
![]() $(a) \to I$
, is an isomorphism.
$(a) \to I$
, is an isomorphism.
Proof. The natural inclusion
![]() $0\to (a) \xrightarrow {i} I$
induces the following commutative diagram:
$0\to (a) \xrightarrow {i} I$
induces the following commutative diagram:

where the rows are natural inclusion maps, and the vertical arrows are isomorphisms due to [Reference Kobayashi and Takahashi26, Prop. 2.4(1)]. So, it is enough to show that
![]() $(I:M)\subseteq ((a):M)$
. Indeed, if
$(I:M)\subseteq ((a):M)$
. Indeed, if
![]() $x\in (I:M)$
, then
$x\in (I:M)$
, then
![]() $xM\subseteq I$
. Since M is I-Ulrich, M is a
$xM\subseteq I$
. Since M is I-Ulrich, M is a
 $B(I)=R\left [\dfrac Ia\right ]$
-module (see [Reference Dao, Maitra and Sridhar11, Rem. 4.4 and Th. 4.6]). Hence,
$B(I)=R\left [\dfrac Ia\right ]$
-module (see [Reference Dao, Maitra and Sridhar11, Rem. 4.4 and Th. 4.6]). Hence,
![]() $\dfrac I a M\subseteq M$
, so
$\dfrac I a M\subseteq M$
, so
![]() $\dfrac I a xM\subseteq xM\subseteq I$
. Thus,
$\dfrac I a xM\subseteq xM\subseteq I$
. Thus,
![]() $\dfrac 1 a xM\subseteq (I:I)=R$
, so
$\dfrac 1 a xM\subseteq (I:I)=R$
, so
![]() $xM\subseteq (a)$
. Therefore,
$xM\subseteq (a)$
. Therefore,
![]() $x\in \left ((a):M\right )$
.
$x\in \left ((a):M\right )$
.
Proposition 5.1.26. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let I be an
$1$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal of R admitting a principal reduction
$\mathfrak {m}$
-primary ideal of R admitting a principal reduction
![]() $a\in I$
. Assume
$a\in I$
. Assume
![]() $(I:I)=R$
. If there exists an I-Ulrich module
$(I:I)=R$
. If there exists an I-Ulrich module
![]() $M\subseteq Q(R)$
, containing a nonzero divisor of R such that
$M\subseteq Q(R)$
, containing a nonzero divisor of R such that
![]() ${\operatorname{Ext}}^1_R(M,R)^{\mu }=0$
, then
${\operatorname{Ext}}^1_R(M,R)^{\mu }=0$
, then
![]() $I\cong R$
.
$I\cong R$
.
Proof. Consider the short exact sequence
![]() $0\to (a) \xrightarrow {i} I \to I/(a)\to 0$
. Since
$0\to (a) \xrightarrow {i} I \to I/(a)\to 0$
. Since
![]() $I^{n+1}=aI^n$
for all
$I^{n+1}=aI^n$
for all
![]() $n\gg 0$
and I contains a nonzero divisor, we have that a is a nonzero divisor. So,
$n\gg 0$
and I contains a nonzero divisor, we have that a is a nonzero divisor. So,
![]() $(a)\cong R$
. If
$(a)\cong R$
. If
![]() $a\in \mathfrak {m} I$
, then
$a\in \mathfrak {m} I$
, then
![]() $I^{n+1}\subseteq \mathfrak {m} II^n=\mathfrak {m} I^{n+1}$
, which implies that
$I^{n+1}\subseteq \mathfrak {m} II^n=\mathfrak {m} I^{n+1}$
, which implies that
![]() $I^{n+1}=0$
by Nakayama’s lemma. This contradicts the fact that I is
$I^{n+1}=0$
by Nakayama’s lemma. This contradicts the fact that I is
![]() $\mathfrak {m}$
-primary. So,
$\mathfrak {m}$
-primary. So,
![]() $a\notin \mathfrak {m} I$
, and hence
$a\notin \mathfrak {m} I$
, and hence
![]() $\mu (I/(a))=\mu (I)-1$
. Thus, the above short exact sequence is
$\mu (I/(a))=\mu (I)-1$
. Thus, the above short exact sequence is
![]() $\mu $
-additive. So, by Corollary 3.9, we get the following induced exact sequence:
$\mu $
-additive. So, by Corollary 3.9, we get the following induced exact sequence:
where the induced map
![]() $ \operatorname{Hom}_R(M,(a))\to \operatorname{Hom}_R(M,I)$
is an isomorphism by Lemma 5.1.25. Hence, we get
$ \operatorname{Hom}_R(M,(a))\to \operatorname{Hom}_R(M,I)$
is an isomorphism by Lemma 5.1.25. Hence, we get
![]() $\operatorname{Hom}_R(M,I/(a))=0$
. Now,
$\operatorname{Hom}_R(M,I/(a))=0$
. Now,
![]() $I/(a)$
has finite length. So, if
$I/(a)$
has finite length. So, if
![]() $I/(a)\ne 0$
, then
$I/(a)\ne 0$
, then
![]() $\operatorname{Ass}(I/(a))=\{\mathfrak {m}\}$
. Hence,
$\operatorname{Ass}(I/(a))=\{\mathfrak {m}\}$
. Hence,
![]() $\operatorname{Ass}\left (\operatorname{Hom}_R(M,I/(a))\right )=\operatorname{Supp}(M)\cap \operatorname{Ass}(I/(a))=\operatorname{Supp}(M)\cap \{\mathfrak {m}\}=\{\mathfrak {m}\}$
, contradicting
$\operatorname{Ass}\left (\operatorname{Hom}_R(M,I/(a))\right )=\operatorname{Supp}(M)\cap \operatorname{Ass}(I/(a))=\operatorname{Supp}(M)\cap \{\mathfrak {m}\}=\{\mathfrak {m}\}$
, contradicting
![]() $\operatorname{Hom}_R(M,I/(a))=0$
. Thus, we must have
$\operatorname{Hom}_R(M,I/(a))=0$
. Thus, we must have
![]() $I/(a)=0$
, that is,
$I/(a)=0$
, that is,
![]() $I=(a)\cong R$
.
$I=(a)\cong R$
.
5.2 Some applications of the subfunctor
 ${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(-,-)$
${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(-,-)$
Let I be an
![]() $\mathfrak {m}$
-primary ideal. In this subsection, we give various applications of the subfunctor
$\mathfrak {m}$
-primary ideal. In this subsection, we give various applications of the subfunctor
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(-,-):\operatorname{Ul}_I^s (R)^{op}\times \operatorname{Ul}_I^s(R) \to {\operatorname{mod}}\ R$
(see 4.9 for notation), where we recall from Corollary 4.7 that
${\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(-,-):\operatorname{Ul}_I^s (R)^{op}\times \operatorname{Ul}_I^s(R) \to {\operatorname{mod}}\ R$
(see 4.9 for notation), where we recall from Corollary 4.7 that
![]() $\operatorname{Ul}_I^s(R)$
along with its all short exact sequences form an exact subcategory of
$\operatorname{Ul}_I^s(R)$
along with its all short exact sequences form an exact subcategory of
![]() ${\operatorname{mod}}\ R$
. Hence,
${\operatorname{mod}}\ R$
. Hence,
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(-,-):\operatorname{Ul}_I^s (R)^{op}\times \operatorname{Ul}_I^s(R) \to {\operatorname{mod}}\ R$
is a subfunctor of
${\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(-,-):\operatorname{Ul}_I^s (R)^{op}\times \operatorname{Ul}_I^s(R) \to {\operatorname{mod}}\ R$
is a subfunctor of
![]() ${\operatorname{Ext}}^1_R(-,-):\operatorname{Ul}_I^s (R)^{op}\times \operatorname{Ul}_I^s(R) \to {\operatorname{mod}}\ R$
by Proposition 3.8.
${\operatorname{Ext}}^1_R(-,-):\operatorname{Ul}_I^s (R)^{op}\times \operatorname{Ul}_I^s(R) \to {\operatorname{mod}}\ R$
by Proposition 3.8.
We begin by observing a general connection between
![]() ${\operatorname{Ext}}^1_R(M,N)$
and
${\operatorname{Ext}}^1_R(M,N)$
and
![]() ${\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
, where
${\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
, where
![]() $M,N\in {\operatorname{mod}}\ R$
and
$M,N\in {\operatorname{mod}}\ R$
and
![]() $\nu _I(-):=\lambda ((-)\otimes _R R/I):{\operatorname{mod}}\ R\to \mathbb Z$
and (see Definition 4.10 for notation of
$\nu _I(-):=\lambda ((-)\otimes _R R/I):{\operatorname{mod}}\ R\to \mathbb Z$
and (see Definition 4.10 for notation of
![]() ${\operatorname{Ext}}^1_R(-,-)^{\phi }$
).
${\operatorname{Ext}}^1_R(-,-)^{\phi }$
).
Lemma 5.2.1. Let
![]() $(R,\mathfrak {m})$
be a Noetherian local ring, and let I be an
$(R,\mathfrak {m})$
be a Noetherian local ring, and let I be an
![]() $\mathfrak {m}$
-primary ideal. Then,
$\mathfrak {m}$
-primary ideal. Then,
![]() $I\ {\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
for all
$I\ {\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
for all
![]() $M,N\in {\operatorname{mod}}\ R$
.
$M,N\in {\operatorname{mod}}\ R$
.
Proof. Let
![]() $\sigma :0\to N \to X \to M \to 0$
be a short exact sequence in
$\sigma :0\to N \to X \to M \to 0$
be a short exact sequence in
![]() $I\ {\operatorname{Ext}}^1_R(M,N)$
. Then
$I\ {\operatorname{Ext}}^1_R(M,N)$
. Then
![]() $\sigma \otimes _R R/I$
splits by [Reference Striuli36, Th. 1.1], so
$\sigma \otimes _R R/I$
splits by [Reference Striuli36, Th. 1.1], so
![]() $M/IM \oplus N/IN \cong X/IX$
. Hence, taking length, we get
$M/IM \oplus N/IN \cong X/IX$
. Hence, taking length, we get
![]() $\lambda (M/IM)+\lambda (N/IN)=\lambda (X/IX)$
, so
$\lambda (M/IM)+\lambda (N/IN)=\lambda (X/IX)$
, so
![]() $\sigma $
is
$\sigma $
is
![]() $\nu _I$
-additive.
$\nu _I$
-additive.
This allows us to prove a general connection between
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
and
${\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
and
![]() ${\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
, when
${\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
, when
![]() $M,N\in \operatorname{Ul}^s_I(R)$
(recall the definition of
$M,N\in \operatorname{Ul}^s_I(R)$
(recall the definition of
![]() $\operatorname{Ul}^s_I(R)$
from Definition 4.5).
$\operatorname{Ul}^s_I(R)$
from Definition 4.5).
Lemma 5.2.2. Let
![]() $(R,\mathfrak {m})$
be a local ring, let
$(R,\mathfrak {m})$
be a local ring, let
![]() $s\ge 0$
be an integer, and let I be an
$s\ge 0$
be an integer, and let I be an
![]() $\mathfrak {m}$
-primary ideal. Then,
$\mathfrak {m}$
-primary ideal. Then,
![]() ${\operatorname{Ext}}^1_R(M,N)^{\nu _I}={\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
for all
${\operatorname{Ext}}^1_R(M,N)^{\nu _I}={\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
for all
![]() $M,N\in \operatorname{Ul}^s_I(R)$
. So, in particular,
$M,N\in \operatorname{Ul}^s_I(R)$
. So, in particular,
![]() $I{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(M,N)$
for all
$I{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(M,N)$
for all
![]() $M,N\in \operatorname{Ul}^s_I(R)$
.
$M,N\in \operatorname{Ul}^s_I(R)$
.
Proof. Let
![]() $M,N\in \operatorname{Ul}^s_I(R)$
, and let
$M,N\in \operatorname{Ul}^s_I(R)$
, and let
![]() $\sigma : 0\to N \to X \to M \to 0$
be a short exact sequence of R-modules. Then
$\sigma : 0\to N \to X \to M \to 0$
be a short exact sequence of R-modules. Then
![]() $X\in \operatorname{CM}^s(R)$
(see 4.2), and
$X\in \operatorname{CM}^s(R)$
(see 4.2), and
![]() $\lambda (M/IM)+\lambda (N/IN)=e_R(I,M)+e_R(I,N)=e_R(I,X)$
. Now,
$\lambda (M/IM)+\lambda (N/IN)=e_R(I,M)+e_R(I,N)=e_R(I,X)$
. Now,
![]() $\sigma \in {\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
, if and only if
$\sigma \in {\operatorname{Ext}}^1_R(M,N)^{\nu _I}$
, if and only if
![]() $\lambda (X/IX)=\lambda (M/IM)+\lambda (N/IN)$
, if and only if
$\lambda (X/IX)=\lambda (M/IM)+\lambda (N/IN)$
, if and only if
![]() $\lambda (X/IX)=e_R(I,X)$
, if and only if
$\lambda (X/IX)=e_R(I,X)$
, if and only if
![]() $X\in \operatorname{Ul}^s_I(R)$
if and only if
$X\in \operatorname{Ul}^s_I(R)$
if and only if
![]() $\sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(M,N)$
. This proves the desired equality
$\sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}_I^s(R)}(M,N)$
. This proves the desired equality
![]() ${\operatorname{Ext}}^1_R(M,N)^{\nu _I}={\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
. The last inclusion in the statement now follows from this and Lemma 5.2.1.
${\operatorname{Ext}}^1_R(M,N)^{\nu _I}={\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
. The last inclusion in the statement now follows from this and Lemma 5.2.1.
When R is Cohen–Macaulay of dimension
![]() $1$
and
$1$
and
![]() $M,N\in \operatorname{Ul}_I(R)$
, then one can improve the inclusion
$M,N\in \operatorname{Ul}_I(R)$
, then one can improve the inclusion
![]() $I{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
of Lemma 5.2.2 quite a bit. For this, we first record a general lemma about trace ideals. In the following, we say that
$I{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
of Lemma 5.2.2 quite a bit. For this, we first record a general lemma about trace ideals. In the following, we say that
![]() $\dfrac {a}{b}\in Q(R)$
is a nonzero divisor if a is a nonzero divisor in R. Note that this does not depend on the choice of representative, since
$\dfrac {a}{b}\in Q(R)$
is a nonzero divisor if a is a nonzero divisor in R. Note that this does not depend on the choice of representative, since
![]() $\frac ab=\frac {a'} {b'}$
in
$\frac ab=\frac {a'} {b'}$
in
![]() $Q(R)$
implies
$Q(R)$
implies
![]() $ab'=a'b$
, and since
$ab'=a'b$
, and since
![]() $b,b'$
are nonzero divisors in R, so a is a nonzero divisor in R if and only if
$b,b'$
are nonzero divisors in R, so a is a nonzero divisor in R if and only if
![]() $a'$
is a nonzero divisor in R.
$a'$
is a nonzero divisor in R.
Lemma 5.2.3. Let I be an ideal of R containing a nonzero divisor. Then the following holds:
-
(1) There exist nonzero divisors
 $x_1,...,x_n\in R$
such that
$x_1,...,x_n\in R$
such that
 $I=(x_1,...,x_n)$
.
$I=(x_1,...,x_n)$
. -
(2) There exist nonzero divisors
 $y_1,...,y_n \in (R:I)$
such that
$y_1,...,y_n \in (R:I)$
such that
 $\operatorname{tr}_R(I)=\sum _{i=1}^n y_iI$
.
$\operatorname{tr}_R(I)=\sum _{i=1}^n y_iI$
.
Proof. (1) Let S be the collection of all nonzero divisors of R that are in I. Let
![]() $\langle S\rangle $
be the ideal of R generated by S. Then
$\langle S\rangle $
be the ideal of R generated by S. Then
![]() $I\subseteq (\cup _{\mathfrak {p}\in \operatorname{Ass}(R)} \mathfrak {p}) \cup \langle S\rangle $
. By prime avoidance, either
$I\subseteq (\cup _{\mathfrak {p}\in \operatorname{Ass}(R)} \mathfrak {p}) \cup \langle S\rangle $
. By prime avoidance, either
![]() $I \subseteq \mathfrak {p}$
for some
$I \subseteq \mathfrak {p}$
for some
![]() $\mathfrak {p} \in \operatorname{Ass}(R)$
, or
$\mathfrak {p} \in \operatorname{Ass}(R)$
, or
![]() $I\subseteq \langle S\rangle $
. But I contains a nonzero divisor, so
$I\subseteq \langle S\rangle $
. But I contains a nonzero divisor, so
![]() $I\nsubseteq \mathfrak {p}$
for every
$I\nsubseteq \mathfrak {p}$
for every
![]() $\mathfrak {p}\in \operatorname{Ass}(R)$
. Hence,
$\mathfrak {p}\in \operatorname{Ass}(R)$
. Hence,
![]() $I\subseteq \langle S\rangle $
. Since S is a subset of I, we conclude
$I\subseteq \langle S\rangle $
. Since S is a subset of I, we conclude
![]() $I= \langle S\rangle $
. Since R is Noetherian, there exist finitely many elements
$I= \langle S\rangle $
. Since R is Noetherian, there exist finitely many elements
![]() $x_1,...,x_n\in S$
such that
$x_1,...,x_n\in S$
such that
![]() $I=(x_1,...,x_n)$
.
$I=(x_1,...,x_n)$
.
(2) We know that
![]() $\operatorname{tr}_R(I)=(R:I)I$
in
$\operatorname{tr}_R(I)=(R:I)I$
in
![]() $Q(R)$
(see [Reference Kobayashi and Takahashi26, Prop. 2.4(2)]). Pick a nonzero divisor
$Q(R)$
(see [Reference Kobayashi and Takahashi26, Prop. 2.4(2)]). Pick a nonzero divisor
![]() $a\in I$
, so
$a\in I$
, so
![]() $J=a(R:I)\subseteq R$
is an ideal of R. Then
$J=a(R:I)\subseteq R$
is an ideal of R. Then
![]() $\operatorname{tr}_R(I)=J(\frac 1 aI)$
. Now, J contains a nonzero divisor, so by part (1), we have
$\operatorname{tr}_R(I)=J(\frac 1 aI)$
. Now, J contains a nonzero divisor, so by part (1), we have
![]() $J=(x_1,...,x_n)$
for some nonzero divisors
$J=(x_1,...,x_n)$
for some nonzero divisors
![]() $x_1,...,x_n$
. Then
$x_1,...,x_n$
. Then
![]() $\operatorname{tr}_R(I)=\sum _{i=1}^n \frac 1 a x_iI$
. Denoting
$\operatorname{tr}_R(I)=\sum _{i=1}^n \frac 1 a x_iI$
. Denoting
![]() $y_i:=\frac 1 a x_i$
, we see that each
$y_i:=\frac 1 a x_i$
, we see that each
![]() $y_i\in Q(R)$
is a nonzero divisor, and
$y_i\in Q(R)$
is a nonzero divisor, and
![]() $y_i\in (R:I)$
as
$y_i\in (R:I)$
as
![]() $x_i\in a(R:I)$
. Hence the claim.
$x_i\in a(R:I)$
. Hence the claim.
In the proof of the next result, for an
![]() $\mathfrak {m}$
-primary ideal I,
$\mathfrak {m}$
-primary ideal I,
![]() $B(I)$
denotes blow-up of I in the sense of [Reference Dao, Maitra and Sridhar11, Def. 4.3 and Rem. 4.4], namely
$B(I)$
denotes blow-up of I in the sense of [Reference Dao, Maitra and Sridhar11, Def. 4.3 and Rem. 4.4], namely
![]() $B(I) :=\cup _{n>0}(I^n:_{Q(R)} I^n)$
.
$B(I) :=\cup _{n>0}(I^n:_{Q(R)} I^n)$
.
Proposition 5.2.4. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
, and let I be an
$1$
, and let I be an
![]() $\mathfrak {m}$
-primary ideal of R. Then
$\mathfrak {m}$
-primary ideal of R. Then
![]() $\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
for all
$\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
for all
![]() $M,N\in \operatorname{Ul}_I(R)$
.
$M,N\in \operatorname{Ul}_I(R)$
.
Proof. Let
![]() $M,N\in \operatorname{Ul}_I(R)$
, and let
$M,N\in \operatorname{Ul}_I(R)$
, and let
![]() $a\in (R:I)$
be a nonzero divisor. Then
$a\in (R:I)$
be a nonzero divisor. Then
![]() $aI$
is an
$aI$
is an
![]() $\mathfrak {m}$
-primary ideal of R and
$\mathfrak {m}$
-primary ideal of R and
![]() $B(I)=B(aI)$
. So,
$B(I)=B(aI)$
. So,
![]() $\operatorname{Ul}_I(R)=\operatorname{Ul}_{aI}(R)$
by [Reference Dao, Maitra and Sridhar11, Prop. 4.24]. Hence, for every nonzero divisor
$\operatorname{Ul}_I(R)=\operatorname{Ul}_{aI}(R)$
by [Reference Dao, Maitra and Sridhar11, Prop. 4.24]. Hence, for every nonzero divisor
![]() $a\in (R:I)$
, we have
$a\in (R:I)$
, we have
![]() $aI{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
by Lemma 5.2.2. Now, by Lemma 5.2.3, there exist nonzero divisors
$aI{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
by Lemma 5.2.2. Now, by Lemma 5.2.3, there exist nonzero divisors
![]() $y_1,...,y_n\in (R:I)$
such that
$y_1,...,y_n\in (R:I)$
such that
![]() $\operatorname{tr}_R(I)=\sum _{i=1}^n y_iI$
. Thus,
$\operatorname{tr}_R(I)=\sum _{i=1}^n y_iI$
. Thus,
![]() $\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,N)= \sum _{i=1}^n y_iI{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
.
$\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,N)= \sum _{i=1}^n y_iI{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
.
When
![]() $s=1$
,
$s=1$
,
![]() $\operatorname{depth} R>0$
, and
$\operatorname{depth} R>0$
, and
![]() $I=\mathfrak {m}$
(so
$I=\mathfrak {m}$
(so
![]() $\nu _I(-)=\mu (-)$
), the inclusion
$\nu _I(-)=\mu (-)$
), the inclusion
![]() $I{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
of Lemma 5.2.2 is actually an equality as we prove next. For this, we first record an easy lemma about flat extensions.
$I{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}^s_I(R)}(M,N)$
of Lemma 5.2.2 is actually an equality as we prove next. For this, we first record an easy lemma about flat extensions.
Lemma 5.2.5. Let
![]() $R\to S$
be a flat extension of rings. Let M be an R-module, and let I an ideal of R. Then, the following holds:
$R\to S$
be a flat extension of rings. Let M be an R-module, and let I an ideal of R. Then, the following holds:
-
(1)
 $S \otimes _R (IM)=(IS)(S \otimes _R M)$
when identified as submodules of
$S \otimes _R (IM)=(IS)(S \otimes _R M)$
when identified as submodules of
 $S\otimes _R M$
.
$S\otimes _R M$
. -
(2) If
 $N\subseteq M$
is an R-submodule, S is a faithfully flat extension of R, and
$N\subseteq M$
is an R-submodule, S is a faithfully flat extension of R, and
 $S \otimes _R M=S \otimes _R N$
, then
$S \otimes _R M=S \otimes _R N$
, then
 $M=N$
.
$M=N$
.
Proof. (1) Consider the exact sequence
![]() $0\to IM \to M \to M/IM\to 0$
, which after tensoring with S gives
$0\to IM \to M \to M/IM\to 0$
, which after tensoring with S gives
![]() $0\to S \otimes _R (IM) \to S\otimes _R M \to S\otimes _R M/IM \to 0$
. Now,
$0\to S \otimes _R (IM) \to S\otimes _R M \to S\otimes _R M/IM \to 0$
. Now,
![]() $S \otimes _R M/IM \cong S \otimes _R (M\otimes _R R/I)\cong (S\otimes _R M)\otimes _R R/I\cong (S\otimes _R M)/I(S \otimes _R M)$
. Now, by the natural S-module structure on
$S \otimes _R M/IM \cong S \otimes _R (M\otimes _R R/I)\cong (S\otimes _R M)\otimes _R R/I\cong (S\otimes _R M)/I(S \otimes _R M)$
. Now, by the natural S-module structure on
![]() $S\otimes _R M$
, we see that
$S\otimes _R M$
, we see that
![]() $I(S \otimes _R M)=(IS)(S \otimes _R M)$
. Thus, we get the exact sequence
$I(S \otimes _R M)=(IS)(S \otimes _R M)$
. Thus, we get the exact sequence
![]() $0\to S \otimes _R (IM) \to S\otimes _R M \to (S \otimes _R M)/(IS)(S \otimes _R M)\to 0$
, and by naturality of the isomorphisms, we see that the map
$0\to S \otimes _R (IM) \to S\otimes _R M \to (S \otimes _R M)/(IS)(S \otimes _R M)\to 0$
, and by naturality of the isomorphisms, we see that the map
![]() $S\otimes _R M \to (S \otimes _R M)/(IS)(S \otimes _R M)$
in the exact sequence has kernel
$S\otimes _R M \to (S \otimes _R M)/(IS)(S \otimes _R M)$
in the exact sequence has kernel
![]() $(IS)(S \otimes _R M)$
. Hence,
$(IS)(S \otimes _R M)$
. Hence,
![]() $S \otimes _R (IM)=(IS)(S \otimes _R M).$
$S \otimes _R (IM)=(IS)(S \otimes _R M).$
(2) Tensoring the exact sequence
![]() $0\to N \to M \to M/N \to 0$
with S and using
$0\to N \to M \to M/N \to 0$
with S and using
![]() $S \otimes _R M=S \otimes _R N$
, we get
$S \otimes _R M=S \otimes _R N$
, we get
![]() $(M/N)\otimes _R S=0$
. Since S is faithfully flat, we have
$(M/N)\otimes _R S=0$
. Since S is faithfully flat, we have
![]() $M/N=0$
. Hence,
$M/N=0$
. Hence,
![]() $M=N$
.
$M=N$
.
Now, we prove the desired equality between
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
and
$\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
and
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
, when R has positive depth.
${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
, when R has positive depth.
Proposition 5.2.6. Let
![]() $(R,\mathfrak {m},k)$
be a local ring of positive depth. Let
$(R,\mathfrak {m},k)$
be a local ring of positive depth. Let
![]() $M,N\in \operatorname{Ul}^1(R)$
. Then, the following holds:
$M,N\in \operatorname{Ul}^1(R)$
. Then, the following holds:
-
(1) We always have
 $\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)={\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
.
$\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)={\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
. -
(2) If R is moreover Cohen–Macaulay of dimension
 $1$
(so
$1$
(so
 $\operatorname{Ul}^1(R)=\operatorname{Ul}(R)$
) and if
$\operatorname{Ul}^1(R)=\operatorname{Ul}(R)$
) and if
 $x\in \mathfrak {m}$
is a minimal reduction of
$x\in \mathfrak {m}$
is a minimal reduction of
 $\mathfrak {m}$
, then
$\mathfrak {m}$
, then
 $x{\operatorname{Ext}}^1_R(M,N)={\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N)$
.
$x{\operatorname{Ext}}^1_R(M,N)={\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N)$
.
Proof. (1) Due to Lemma 5.2.2, we only need to prove
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N) \subseteq \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
. We may assume
${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N) \subseteq \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
. We may assume
![]() $M,N\ne 0$
.
$M,N\ne 0$
.
First, we assume that the residue field is infinite. Let
![]() $\sigma : 0\to N\to X\to M\to 0$
be a short exact sequence such that
$\sigma : 0\to N\to X\to M\to 0$
be a short exact sequence such that
![]() $X\in \operatorname{Ul}^1(R)$
. Choose
$X\in \operatorname{Ul}^1(R)$
. Choose
![]() $x\in \mathfrak {m}$
to be
$x\in \mathfrak {m}$
to be
![]() $R\oplus M \oplus N\oplus X$
-superficial (which exists by [Reference Huneke and Swanson24, Prop. 8.5.7], since we are assuming R has infinite residue field). Now,
$R\oplus M \oplus N\oplus X$
-superficial (which exists by [Reference Huneke and Swanson24, Prop. 8.5.7], since we are assuming R has infinite residue field). Now,
![]() $\operatorname{depth}_R(R\oplus M\oplus N\oplus X)=\inf \{\operatorname{depth} R,\operatorname{depth}_R M,\operatorname{depth}_R N,\operatorname{depth}_R X\}>0$
, so x is
$\operatorname{depth}_R(R\oplus M\oplus N\oplus X)=\inf \{\operatorname{depth} R,\operatorname{depth}_R M,\operatorname{depth}_R N,\operatorname{depth}_R X\}>0$
, so x is
![]() $R\oplus M\oplus N\oplus X$
-regular by [Reference Huneke and Swanson24, Lem. 8.5.4]. Hence,
$R\oplus M\oplus N\oplus X$
-regular by [Reference Huneke and Swanson24, Lem. 8.5.4]. Hence,
![]() $x\in \mathfrak {m}$
is regular on
$x\in \mathfrak {m}$
is regular on
![]() $R,M$
, and N, and superficial on
$R,M$
, and N, and superficial on
![]() $M,N$
, and X. Thus,
$M,N$
, and X. Thus,
![]() $M/xM,N/xN,X/xX$
are zero-dimensional Ulrich modules by [Reference Goto, Takahashi and Taniguchi21, Prop. 2.2(4)], so these are k-vector spaces by [Reference Goto, Takahashi and Taniguchi21, Prop. 2.2(1)]. Hence,
$M/xM,N/xN,X/xX$
are zero-dimensional Ulrich modules by [Reference Goto, Takahashi and Taniguchi21, Prop. 2.2(4)], so these are k-vector spaces by [Reference Goto, Takahashi and Taniguchi21, Prop. 2.2(1)]. Hence,
![]() $\sigma \otimes _R R/xR$
, being a short exact sequence of k-vector spaces, is split exact. Since x is
$\sigma \otimes _R R/xR$
, being a short exact sequence of k-vector spaces, is split exact. Since x is
![]() $R,M,N$
-regular, by [Reference Striuli36, Prop. 2.8], we have
$R,M,N$
-regular, by [Reference Striuli36, Prop. 2.8], we have
![]() $\sigma \in x{\operatorname{Ext}}^1_R(M,N)\subseteq \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
.
$\sigma \in x{\operatorname{Ext}}^1_R(M,N)\subseteq \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
.
Now, we prove the general case. This part will use extensively that
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
is a submodule of
${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
is a submodule of
![]() ${\operatorname{Ext}}^1_R(M,N)$
, where
${\operatorname{Ext}}^1_R(M,N)$
, where
![]() $M,N\in \operatorname{Ul}^1(R)$
. Consider the faithfully flat extension of R as follows:
$M,N\in \operatorname{Ul}^1(R)$
. Consider the faithfully flat extension of R as follows:
![]() $S :=R[X]_{\mathfrak {m}[X]}$
, with maximal ideal
$S :=R[X]_{\mathfrak {m}[X]}$
, with maximal ideal
![]() $\mathfrak {m} S$
, and infinite residue field. Since we already know,
$\mathfrak {m} S$
, and infinite residue field. Since we already know,
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
by Lemma 5.2.2 and since S is faithfully flat, it is enough to prove
$\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
by Lemma 5.2.2 and since S is faithfully flat, it is enough to prove
![]() $S\otimes _R \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)=S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
(by Lemma 5.2.5(2)). Now,
$S\otimes _R \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)=S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
(by Lemma 5.2.5(2)). Now,
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
, with flatness of S, already implies
$\mathfrak {m}{\operatorname{Ext}}^1_R(M,N)\subseteq {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
, with flatness of S, already implies
![]() $S \otimes _R \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)\subseteq S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
. So, to prove equality, it is enough to prove that
$S \otimes _R \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)\subseteq S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
. So, to prove equality, it is enough to prove that
![]() $S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N) \subseteq S\otimes _R \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
. Now, due to Lemma 5.2.5(1), it is enough to prove
$S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N) \subseteq S\otimes _R \mathfrak {m}{\operatorname{Ext}}^1_R(M,N)$
. Now, due to Lemma 5.2.5(1), it is enough to prove
![]() $S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N) \subseteq (\mathfrak {m} S)(S \otimes _R {\operatorname{Ext}}^1_R(M,N))$
, and the latter object here is naturally identified with
$S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N) \subseteq (\mathfrak {m} S)(S \otimes _R {\operatorname{Ext}}^1_R(M,N))$
, and the latter object here is naturally identified with
![]() $(\mathfrak {m} S){\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
. Since the S-module
$(\mathfrak {m} S){\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
. Since the S-module
![]() $S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
is generated by
$S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
is generated by
![]() $1\otimes _R \sigma $
as
$1\otimes _R \sigma $
as
![]() $\sigma $
runs over all elements of
$\sigma $
runs over all elements of
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
, we need to prove that
${\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
, we need to prove that
![]() $1 \otimes _R \sigma \in (\mathfrak {m} S){\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
for all
$1 \otimes _R \sigma \in (\mathfrak {m} S){\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
for all
![]() $\sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
. So, let
$\sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)$
. So, let
![]() $\sigma : 0\to N\to X\to M\to 0$
be a short exact sequence such that
$\sigma : 0\to N\to X\to M\to 0$
be a short exact sequence such that
![]() $X\in \operatorname{Ul}^1(R)$
. Then,
$X\in \operatorname{Ul}^1(R)$
. Then,
![]() $1\otimes _R \sigma \in S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)\subseteq S \otimes _R {\operatorname{Ext}}^1_R(M,N)\cong {\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
is naturally identified with the exact sequence
$1\otimes _R \sigma \in S \otimes _R {\operatorname{Ext}}^1_{\operatorname{Ul}^1(R)}(M,N)\subseteq S \otimes _R {\operatorname{Ext}}^1_R(M,N)\cong {\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
is naturally identified with the exact sequence
![]() $S \otimes _R \sigma : 0\to S \otimes _R N \to S \otimes _R X \to S \otimes _R M \to 0$
in
$S \otimes _R \sigma : 0\to S \otimes _R N \to S \otimes _R X \to S \otimes _R M \to 0$
in
![]() ${\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
. Now,
${\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
. Now,
![]() $S \otimes _R \sigma $
is a short exact sequence of modules in
$S \otimes _R \sigma $
is a short exact sequence of modules in
![]() $\operatorname{Ul}^1(S)$
by [Reference Goto, Takahashi and Taniguchi21, Prop. 2.2(3)]. Hence,
$\operatorname{Ul}^1(S)$
by [Reference Goto, Takahashi and Taniguchi21, Prop. 2.2(3)]. Hence,
![]() $1\otimes _R \sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}^1(S)}(S \otimes _R M, S \otimes _R N)$
. Since S also has positive depth and infinite residue field, by the proof of the infinite residue field case, we get
$1\otimes _R \sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}^1(S)}(S \otimes _R M, S \otimes _R N)$
. Since S also has positive depth and infinite residue field, by the proof of the infinite residue field case, we get
![]() $1\otimes _R \sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}^1(S)}(S \otimes _R M, S \otimes _R N) \subseteq (\mathfrak {m} S){\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
, which is what we wanted to prove.
$1\otimes _R \sigma \in {\operatorname{Ext}}^1_{\operatorname{Ul}^1(S)}(S \otimes _R M, S \otimes _R N) \subseteq (\mathfrak {m} S){\operatorname{Ext}}^1_S(S \otimes _R M, S \otimes _R N)$
, which is what we wanted to prove.
(2) Due to Lemma 5.2.2, we only need to prove
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N) \subseteq x{\operatorname{Ext}}^1_R(M,N)$
. So, let
${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N) \subseteq x{\operatorname{Ext}}^1_R(M,N)$
. So, let
![]() $\sigma : 0\to N\to X\to M\to 0$
be a short exact sequence such that
$\sigma : 0\to N\to X\to M\to 0$
be a short exact sequence such that
![]() $X\in \operatorname{Ul}(R)$
. Since
$X\in \operatorname{Ul}(R)$
. Since
![]() $xR$
is a reduction of
$xR$
is a reduction of
![]() $\mathfrak {m}$
, we have
$\mathfrak {m}$
, we have
![]() $xR$
is
$xR$
is
![]() $\mathfrak {m}$
-primary. Hence, x is R-regular, so x is
$\mathfrak {m}$
-primary. Hence, x is R-regular, so x is
![]() $M,N,X$
-regular. Also,
$M,N,X$
-regular. Also,
![]() $\mathfrak {m} M=xM,\mathfrak {m} N=xN,\mathfrak {m} X=xX$
. So,
$\mathfrak {m} M=xM,\mathfrak {m} N=xN,\mathfrak {m} X=xX$
. So,
![]() $\sigma \otimes _R R/xR: 0\to N/xN \to X/xX \to M/xM\to 0$
is an exact sequence of k-vector spaces. Hence,
$\sigma \otimes _R R/xR: 0\to N/xN \to X/xX \to M/xM\to 0$
is an exact sequence of k-vector spaces. Hence,
![]() $\sigma \otimes _R R/xR$
is split exact. Since x is
$\sigma \otimes _R R/xR$
is split exact. Since x is
![]() $R,M,N,X$
-regular, by [Reference Striuli36, Prop. 2.8], we have
$R,M,N,X$
-regular, by [Reference Striuli36, Prop. 2.8], we have
![]() $\sigma \in x{\operatorname{Ext}}^1_R(M,N)$
. Thus, we get
$\sigma \in x{\operatorname{Ext}}^1_R(M,N)$
. Thus, we get
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N) \subseteq x{\operatorname{Ext}}^1_R(M,N)$
.
${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N) \subseteq x{\operatorname{Ext}}^1_R(M,N)$
.
Following is an interesting consequence of Proposition 5.2.6. Here, for R-modules
![]() $X,Y$
, we denote by
$X,Y$
, we denote by
![]() $X*Y$
the collection of all R-modules Z that fit into a short exact sequence
$X*Y$
the collection of all R-modules Z that fit into a short exact sequence
![]() $0\to X \to Z \to Y \to 0 $
.
$0\to X \to Z \to Y \to 0 $
.
Corollary 5.2.7. Let
![]() $(R,\mathfrak {m})$
be a local one-dimensional Cohen–Macaulay ring. Then, the following are equivalent:
$(R,\mathfrak {m})$
be a local one-dimensional Cohen–Macaulay ring. Then, the following are equivalent:
-
(1) R is regular.
-
(2)
 $\operatorname{Ul}(R)$
is closed under taking extensions.
$\operatorname{Ul}(R)$
is closed under taking extensions. -
(3) There exists
 $M,N\in \operatorname{Ul}(R)$
such that N is faithful,
$M,N\in \operatorname{Ul}(R)$
such that N is faithful,
 $M\ne 0$
, and
$M\ne 0$
, and
 $N*M\subseteq \operatorname{Ul}(R)$
.
$N*M\subseteq \operatorname{Ul}(R)$
.
Proof.
![]() $(1)\implies (2)$
: If R is regular, then
$(1)\implies (2)$
: If R is regular, then
![]() $\operatorname{Ul}(R)=\operatorname{CM}(R)$
, which is closed under taking extensions.
$\operatorname{Ul}(R)=\operatorname{CM}(R)$
, which is closed under taking extensions.
![]() $(2)\implies (3)$
: One can take
$(2)\implies (3)$
: One can take
![]() $M=N=\mathfrak {m}^n$
for some
$M=N=\mathfrak {m}^n$
for some
![]() $n\gg 0$
.
$n\gg 0$
.
![]() $(3) \implies (1)$
: By hypothesis, we get
$(3) \implies (1)$
: By hypothesis, we get
![]() ${\operatorname{Ext}}^1_{R}(M,N)={\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N)$
. Then from Proposition 5.2.6 (remembering
${\operatorname{Ext}}^1_{R}(M,N)={\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N)$
. Then from Proposition 5.2.6 (remembering
![]() $\operatorname{Ul}^1(R)=\operatorname{Ul}(R)$
in our case), we get
$\operatorname{Ul}^1(R)=\operatorname{Ul}(R)$
in our case), we get
![]() ${\operatorname{Ext}}^1_{R}(M,N)=\mathfrak {m}{\operatorname{Ext}}^1_{R}(M,N)$
. So, by Nakayama’s lemma, we get
${\operatorname{Ext}}^1_{R}(M,N)=\mathfrak {m}{\operatorname{Ext}}^1_{R}(M,N)$
. So, by Nakayama’s lemma, we get
![]() ${\operatorname{Ext}}^1_{R}(M,N)=0$
. By [Reference Dao, Maitra and Sridhar11, Th. 4.6] (see also [Reference Dey and Kobayashi12, Lem. 5.2]), we get
${\operatorname{Ext}}^1_{R}(M,N)=0$
. By [Reference Dao, Maitra and Sridhar11, Th. 4.6] (see also [Reference Dey and Kobayashi12, Lem. 5.2]), we get
![]() $M\cong \mathfrak {m} M$
and
$M\cong \mathfrak {m} M$
and
![]() $N\cong \mathfrak {m} N$
. So,
$N\cong \mathfrak {m} N$
. So,
![]() ${\operatorname{Ext}}^1_R(\mathfrak {m} M,\mathfrak {m} N)=0$
. Hence,
${\operatorname{Ext}}^1_R(\mathfrak {m} M,\mathfrak {m} N)=0$
. Hence,
![]() $\operatorname{pd}_R (\mathfrak {m} M)<\infty $
by [Reference Dey and Kobayashi12, Prop. 2.6]. Thus,
$\operatorname{pd}_R (\mathfrak {m} M)<\infty $
by [Reference Dey and Kobayashi12, Prop. 2.6]. Thus,
![]() $\operatorname{Tor}^R_{\gg 0}(\mathfrak {m}, \mathfrak {m} M)=0$
. Since
$\operatorname{Tor}^R_{\gg 0}(\mathfrak {m}, \mathfrak {m} M)=0$
. Since
![]() $0\ne M$
, we have
$0\ne M$
, we have
![]() $\mathfrak {m} M\cong M\ne 0$
. Thus,
$\mathfrak {m} M\cong M\ne 0$
. Thus,
![]() $\operatorname{pd}_R(\mathfrak {m})<\infty $
by [Reference Dey and Kobayashi12, Cor. 3.17]. Hence, R is regular.
$\operatorname{pd}_R(\mathfrak {m})<\infty $
by [Reference Dey and Kobayashi12, Cor. 3.17]. Hence, R is regular.
We mention in passing that when R is local Cohen–Macaulay of minimal multiplicity,
![]() $(2)\implies (1)$
of Corollary 5.2.7 also follows from [Reference Dey and Takahashi13, Prop. 3.2(5)].
$(2)\implies (1)$
of Corollary 5.2.7 also follows from [Reference Dey and Takahashi13, Prop. 3.2(5)].
Before proceeding further with applications to
![]() $\operatorname{Ul}_I(R)$
, we outline an alternative proof that
$\operatorname{Ul}_I(R)$
, we outline an alternative proof that
![]() $\operatorname{Ul}_I(R)$
is an exact subcategory of
$\operatorname{Ul}_I(R)$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
when R is a local one-dimensional Cohen–Macaulay ring, via birational extensions. For this, we first record some preliminary results.
${\operatorname{mod}}\ R$
when R is a local one-dimensional Cohen–Macaulay ring, via birational extensions. For this, we first record some preliminary results.
The following is easy to see from the definition of an exact category.
Lemma 5.2.8. Let
![]() $R,S$
be two commutative rings such that
$R,S$
be two commutative rings such that
![]() $R\to S$
is a ring extension. Let
$R\to S$
is a ring extension. Let
![]() $({\cal{X}},{\cal{E}})$
be a strictly full exact subcategory of
$({\cal{X}},{\cal{E}})$
be a strictly full exact subcategory of
![]() ${\operatorname{Mod}}\ S$
. Assume that
${\operatorname{Mod}}\ S$
. Assume that
![]() ${\cal{X}}$
is closed under R-linear isomorphism of R-modules. Also, assume that every R-linear map between any two modules in
${\cal{X}}$
is closed under R-linear isomorphism of R-modules. Also, assume that every R-linear map between any two modules in
![]() ${\cal{X}}$
is S-linear, that is,
${\cal{X}}$
is S-linear, that is,
![]() $\operatorname{Hom}_R(M,N)=\operatorname{Hom}_S(M,N)$
for all
$\operatorname{Hom}_R(M,N)=\operatorname{Hom}_S(M,N)$
for all
![]() $M,N\in {\cal{X}}$
. Then,
$M,N\in {\cal{X}}$
. Then,
![]() $({\cal{X}},{\cal{E}})$
is a strictly full exact subcategory of
$({\cal{X}},{\cal{E}})$
is a strictly full exact subcategory of
![]() ${\operatorname{Mod}}\ R$
.
${\operatorname{Mod}}\ R$
.
For the consequences of Lemma 5.2.8, we need the following lemma, which is essentially [Reference Leuschke and Wiegand27, Prop. 4.14(i)]. Before proceeding, we note that for a birational extension
![]() $R\subseteq S\subseteq Q(R)$
and an S-module N, being torsion-free as an S-module and as an R-module are the same.
$R\subseteq S\subseteq Q(R)$
and an S-module N, being torsion-free as an S-module and as an R-module are the same.
Lemma 5.2.9. Let R be a commutative Noetherian ring, and let
![]() $R\subseteq S \subseteq Q(R)$
be a ring extension. Then,
$R\subseteq S \subseteq Q(R)$
be a ring extension. Then,
![]() $\operatorname{Hom}_R(M,N)=\operatorname{Hom}_S(M,N)$
for all
$\operatorname{Hom}_R(M,N)=\operatorname{Hom}_S(M,N)$
for all
![]() $M,N\in {\operatorname{Mod}} (S)$
where N is torsion-free S-module.
$M,N\in {\operatorname{Mod}} (S)$
where N is torsion-free S-module.
Proof.
![]() $\operatorname{Hom}_S(M,N)\subseteq \operatorname{Hom}_R(M,N)$
is clear. Hence, it is enough to show that
$\operatorname{Hom}_S(M,N)\subseteq \operatorname{Hom}_R(M,N)$
is clear. Hence, it is enough to show that
![]() $\operatorname{Hom}_R(M,N)\subseteq \operatorname{Hom}_S(M,N)$
. Let
$\operatorname{Hom}_R(M,N)\subseteq \operatorname{Hom}_S(M,N)$
. Let
![]() $\dfrac a b\in S \subseteq Q(R)$
, where
$\dfrac a b\in S \subseteq Q(R)$
, where
![]() $a,b\in R$
, so
$a,b\in R$
, so
![]() $b\in R$
is a nonzero divisor. Let
$b\in R$
is a nonzero divisor. Let
![]() $m\in M$
and
$m\in M$
and
![]() $f\in \operatorname{Hom}_R(M,N)$
. Then
$f\in \operatorname{Hom}_R(M,N)$
. Then
![]() $b\left (f\left (\dfrac a b m\right )-\dfrac a b f(m)\right )=bf\left (\dfrac a b m\right )-af(m)=f\left (b\dfrac a b m\right )-af(m)=f(am)-af(m)=0$
. Since N is torsion-free and b is a nonzero divisor on R, it is a nonzero divisor on N. So,
$b\left (f\left (\dfrac a b m\right )-\dfrac a b f(m)\right )=bf\left (\dfrac a b m\right )-af(m)=f\left (b\dfrac a b m\right )-af(m)=f(am)-af(m)=0$
. Since N is torsion-free and b is a nonzero divisor on R, it is a nonzero divisor on N. So,
![]() $f\left (\dfrac a b m\right )=\dfrac a b f(m)$
. As
$f\left (\dfrac a b m\right )=\dfrac a b f(m)$
. As
![]() $\dfrac a b\in S, m\in M$
, and
$\dfrac a b\in S, m\in M$
, and
![]() $f\in \operatorname{Hom}_R(M,N)$
were arbitrary, we conclude
$f\in \operatorname{Hom}_R(M,N)$
were arbitrary, we conclude
![]() $\operatorname{Hom}_R(M,N)\subseteq \operatorname{Hom}_S(M,N)$
.
$\operatorname{Hom}_R(M,N)\subseteq \operatorname{Hom}_S(M,N)$
.
Now, as a consequence, we can deduce the following.
Proposition 5.2.10. Let
![]() $R\subseteq S$
be a birational extension (
$R\subseteq S$
be a birational extension (
![]() $S\subseteq Q(R)$
) of commutative rings. Let
$S\subseteq Q(R)$
) of commutative rings. Let
![]() ${\cal{S}}_R$
be the standard exact structure on
${\cal{S}}_R$
be the standard exact structure on
![]() ${\operatorname{mod}}\ R$
. Let
${\operatorname{mod}}\ R$
. Let
![]() ${\cal{X}}$
be the strictly full subcategory of
${\cal{X}}$
be the strictly full subcategory of
![]() ${\operatorname{Mod}} S$
consisting of all torsion-free S-modules. Then it holds that
${\operatorname{Mod}} S$
consisting of all torsion-free S-modules. Then it holds that
![]() ${\cal{S}}_R|_{\cal{X}}={\cal{S}}_S|_{\cal{X}}$
, and
${\cal{S}}_R|_{\cal{X}}={\cal{S}}_S|_{\cal{X}}$
, and
![]() $({\cal{X}}, {\cal{S}}_R|_{\cal{X}})$
is a strictly full exact subcategory of
$({\cal{X}}, {\cal{S}}_R|_{\cal{X}})$
is a strictly full exact subcategory of
![]() ${\operatorname{mod}}\ R$
, and
${\operatorname{mod}}\ R$
, and
![]() $({\cal{X}}\cap {\operatorname{mod}}\ R, {\cal{S}}_R|_{{\cal{X}}\cap {\operatorname{mod}}\ R})$
is an exact subcategory of
$({\cal{X}}\cap {\operatorname{mod}}\ R, {\cal{S}}_R|_{{\cal{X}}\cap {\operatorname{mod}}\ R})$
is an exact subcategory of
![]() ${\operatorname{Mod}}\ R$
(hence, also of
${\operatorname{Mod}}\ R$
(hence, also of
![]() ${\operatorname{mod}}\ R$
).
${\operatorname{mod}}\ R$
).
Proof. By definition,
![]() ${\cal{S}}_R|_{{\operatorname{mod}}\ R\cap {\cal{X}}}={\cal{S}}_R|_{{{\operatorname{mod}}\ R}}\cap {\cal{S}}_R|_{\cal{X}}$
. Since
${\cal{S}}_R|_{{\operatorname{mod}}\ R\cap {\cal{X}}}={\cal{S}}_R|_{{{\operatorname{mod}}\ R}}\cap {\cal{S}}_R|_{\cal{X}}$
. Since
![]() $({\operatorname{mod}}\ R,{\cal{S}}_R|_{{{\operatorname{mod}}\ R}})$
is an exact subcategory of
$({\operatorname{mod}}\ R,{\cal{S}}_R|_{{{\operatorname{mod}}\ R}})$
is an exact subcategory of
![]() ${\operatorname{Mod}}\ R$
, the second part of the statement would readily follow from the first part of the statement and Lemma 3.2. First, we show that
${\operatorname{Mod}}\ R$
, the second part of the statement would readily follow from the first part of the statement and Lemma 3.2. First, we show that
![]() $\cal{X}$
is strictly full in
$\cal{X}$
is strictly full in
![]() ${\operatorname{mod}}\ R$
. If
${\operatorname{mod}}\ R$
. If
![]() $M,N$
are two R-modules and
$M,N$
are two R-modules and
![]() $f:M\to N$
is an R-linear isomorphism and N is moreover a torsion-free S-module extending its R-module structure, then M has an S-module structure, extending its R-module structure, given by
$f:M\to N$
is an R-linear isomorphism and N is moreover a torsion-free S-module extending its R-module structure, then M has an S-module structure, extending its R-module structure, given by
![]() $s\cdot m:=f^{-1}(sf(m))$
for all
$s\cdot m:=f^{-1}(sf(m))$
for all
![]() $s\in S, m \in M$
. Note that, with this structure, M is moreover a torsion-free S-module. Indeed, let
$s\in S, m \in M$
. Note that, with this structure, M is moreover a torsion-free S-module. Indeed, let
![]() $s\in S$
be a nonzero divisor such that
$s\in S$
be a nonzero divisor such that
![]() $s\cdot m=0$
. Then
$s\cdot m=0$
. Then
![]() $sf(m)=f(s\cdot m)=0$
, so
$sf(m)=f(s\cdot m)=0$
, so
![]() $f(m)=0$
as N is S-torsion-free. Thus,
$f(m)=0$
as N is S-torsion-free. Thus,
![]() $m=0$
as f is an isomorphism. Moreover,
$m=0$
as f is an isomorphism. Moreover,
![]() $\operatorname{Hom}_R(M,N)=\operatorname{Hom}_S(M,N)$
for all torsion-free S-modules
$\operatorname{Hom}_R(M,N)=\operatorname{Hom}_S(M,N)$
for all torsion-free S-modules
![]() $M,N$
by Lemma 5.2.9. Consequently, we notice that
$M,N$
by Lemma 5.2.9. Consequently, we notice that
![]() ${\cal{S}}_R|_{{\cal{X}}}={\cal{S}}_S|_{{\cal{X}}}$
. So, to show that
${\cal{S}}_R|_{{\cal{X}}}={\cal{S}}_S|_{{\cal{X}}}$
. So, to show that
![]() $({\cal{X}}, {\cal{S}}_R|_{\cal{X}})$
is an exact subcategory of
$({\cal{X}}, {\cal{S}}_R|_{\cal{X}})$
is an exact subcategory of
![]() ${\operatorname{Mod}}\ R$
, it is enough to show that
${\operatorname{Mod}}\ R$
, it is enough to show that
![]() $({\cal{X}}, {\cal{S}}_S|_{\cal{X}})$
is an exact subcategory of
$({\cal{X}}, {\cal{S}}_S|_{\cal{X}})$
is an exact subcategory of
![]() ${\operatorname{Mod}}\ S$
(by Lemma 5.2.8). Now, it is well known that for any ring S, the subcategory of all S-torsion-free modules is closed under extensions in
${\operatorname{Mod}}\ S$
(by Lemma 5.2.8). Now, it is well known that for any ring S, the subcategory of all S-torsion-free modules is closed under extensions in
![]() ${\operatorname{Mod}}\ S$
. Hence,
${\operatorname{Mod}}\ S$
. Hence,
![]() $({\cal{X}}, {\cal{S}}_S|_{\cal{X}})$
is an exact subcategory of
$({\cal{X}}, {\cal{S}}_S|_{\cal{X}})$
is an exact subcategory of
![]() ${\operatorname{Mod}}\ S$
by Proposition 3.5.
${\operatorname{Mod}}\ S$
by Proposition 3.5.
Corollary 5.2.11. Let R be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let
$1$
. Let
![]() $R\subseteq S$
be a finite birational extension. Then,
$R\subseteq S$
be a finite birational extension. Then,
![]() $(\operatorname{CM}(S),{\cal{S}}_R|_{{\operatorname{CM}(S)}})$
is a strictly full exact subcategory of
$(\operatorname{CM}(S),{\cal{S}}_R|_{{\operatorname{CM}(S)}})$
is a strictly full exact subcategory of
![]() ${\operatorname{mod}}\ R$
.
${\operatorname{mod}}\ R$
.
Proof. We note that
![]() ${\operatorname{mod}} S={\operatorname{Mod}}\ S\cap {\operatorname{mod}}\ R$
. Since S is also one-dimensional Cohen–Macaulay, we have
${\operatorname{mod}} S={\operatorname{Mod}}\ S\cap {\operatorname{mod}}\ R$
. Since S is also one-dimensional Cohen–Macaulay, we have
![]() $\operatorname{CM}(S)=$
collection of all finitely generated torsion-free S-modules
$\operatorname{CM}(S)=$
collection of all finitely generated torsion-free S-modules
![]() $ = $
collection of all torsion-free S-modules
$ = $
collection of all torsion-free S-modules
![]() $\cap {\operatorname{mod}}\ R$
. Hence, the conclusion follows from Proposition 5.2.10.
$\cap {\operatorname{mod}}\ R$
. Hence, the conclusion follows from Proposition 5.2.10.
When
![]() $(R,\mathfrak {m})$
is a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
is a local Cohen–Macaulay ring of dimension
![]() $1$
and I an
$1$
and I an
![]() $\mathfrak {m}$
-primary ideal, then considering the finite birational extension
$\mathfrak {m}$
-primary ideal, then considering the finite birational extension
![]() $R\subseteq B(I)$
, where
$R\subseteq B(I)$
, where
![]() $B(I)$
denotes blow-up of I [Reference Dao, Maitra and Sridhar11, Def. 4.3 and Rem. 4.4], it is shown in [Reference Dao, Maitra and Sridhar11, Th. 4.6] that
$B(I)$
denotes blow-up of I [Reference Dao, Maitra and Sridhar11, Def. 4.3 and Rem. 4.4], it is shown in [Reference Dao, Maitra and Sridhar11, Th. 4.6] that
![]() $\operatorname{CM}(B(I))=\operatorname{Ul}_I(R)$
. Thus, in this particular case, we get another proof of the fact that
$\operatorname{CM}(B(I))=\operatorname{Ul}_I(R)$
. Thus, in this particular case, we get another proof of the fact that
![]() $\operatorname{Ul}_I(R)$
is an exact subcategory of
$\operatorname{Ul}_I(R)$
is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
, which is very different from Corollary 4.7.
${\operatorname{mod}}\ R$
, which is very different from Corollary 4.7.
For further applications, we first record a lemma connecting
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(-,-)$
to
${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(-,-)$
to
![]() ${\operatorname{Ext}}^1_{B(I)}(-,-)$
. Here, we will keep in mind that when
${\operatorname{Ext}}^1_{B(I)}(-,-)$
. Here, we will keep in mind that when
![]() $\dim R=1$
, we write
$\dim R=1$
, we write
![]() $\operatorname{Ul}^1_I(R)=\operatorname{Ul}_I(R)$
in our notation (see Definition 4.5).
$\operatorname{Ul}^1_I(R)=\operatorname{Ul}_I(R)$
in our notation (see Definition 4.5).
Lemma 5.2.12. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let I be an
$1$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal of R. Then, for all I-Ulrich modules
$\mathfrak {m}$
-primary ideal of R. Then, for all I-Ulrich modules
![]() $M,N$
, we have a natural map
$M,N$
, we have a natural map
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)\xrightarrow {[\sigma ]_R \to [\sigma ]_{B(I)}} {\operatorname{Ext}}^1_{B(I)}(M,N)$
, which is an isomorphism of R-modules.
${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)\xrightarrow {[\sigma ]_R \to [\sigma ]_{B(I)}} {\operatorname{Ext}}^1_{B(I)}(M,N)$
, which is an isomorphism of R-modules.
Proof. We recall that
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
is the equivalence class of all short exact sequences
${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
is the equivalence class of all short exact sequences
![]() $0\to N \to X \to M\to 0$
of I-Ulrich modules and R-linear maps. Since
$0\to N \to X \to M\to 0$
of I-Ulrich modules and R-linear maps. Since
![]() $\operatorname{Ul}_I(R)=\operatorname{CM}(B(I))$
[Reference Dao, Maitra and Sridhar11, Th. 4.6], any R-linear map between two Ulrich modules is
$\operatorname{Ul}_I(R)=\operatorname{CM}(B(I))$
[Reference Dao, Maitra and Sridhar11, Th. 4.6], any R-linear map between two Ulrich modules is
![]() $B(I)$
-linear (see [Reference Leuschke and Wiegand27, Prop. 4.14(i)]). Hence, any short exact sequence
$B(I)$
-linear (see [Reference Leuschke and Wiegand27, Prop. 4.14(i)]). Hence, any short exact sequence
![]() $0\to N \to X \to M\to 0$
of I-Ulrich modules and R-linear maps is a short exact sequence of maximal Cohen–Macaulay
$0\to N \to X \to M\to 0$
of I-Ulrich modules and R-linear maps is a short exact sequence of maximal Cohen–Macaulay
![]() $B(I)$
-modules and
$B(I)$
-modules and
![]() $B(I)$
-linear maps, and any R-linear morphism between two short exact sequences of I-Ulrich R-modules is actually a
$B(I)$
-linear maps, and any R-linear morphism between two short exact sequences of I-Ulrich R-modules is actually a
![]() $B(I)$
-morphism. This proves the well-definedness of the map. Injectivity is similarly obvious. To prove surjectivity, we note that if Y is a
$B(I)$
-morphism. This proves the well-definedness of the map. Injectivity is similarly obvious. To prove surjectivity, we note that if Y is a
![]() $B(I)$
-module, and
$B(I)$
-module, and
![]() $0\to N \to Y \to M \to 0$
is a short exact sequence in
$0\to N \to Y \to M \to 0$
is a short exact sequence in
![]() ${\operatorname{Mod}} (B(I))$
, then
${\operatorname{Mod}} (B(I))$
, then
![]() $M,N\in \operatorname{CM}(B(I))$
implies
$M,N\in \operatorname{CM}(B(I))$
implies
![]() $Y\in \operatorname{CM}(B(I))$
. Hence,
$Y\in \operatorname{CM}(B(I))$
. Hence,
![]() $Y\in \operatorname{Ul}_I(R)$
. Since
$Y\in \operatorname{Ul}_I(R)$
. Since
![]() $B(I)$
-linear maps are R-linear, this gives a pre-image in
$B(I)$
-linear maps are R-linear, this gives a pre-image in
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
. Finally, to show the map is R-linear, we recall that the Baer-sum structure and multiplication by R on
${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,N)$
. Finally, to show the map is R-linear, we recall that the Baer-sum structure and multiplication by R on
![]() ${\operatorname{Ext}}^1$
are given by certain pullback and pushout diagrams. So, it is enough to prove that given an exact sequence
${\operatorname{Ext}}^1$
are given by certain pullback and pushout diagrams. So, it is enough to prove that given an exact sequence
![]() $\sigma : 0\to N \to X \to M \to 0$
in
$\sigma : 0\to N \to X \to M \to 0$
in
![]() $\operatorname{Ul}_I(R)$
and R-linear maps
$\operatorname{Ul}_I(R)$
and R-linear maps
![]() $f: N\to N', g:M'\to M$
with
$f: N\to N', g:M'\to M$
with
![]() $M',N'\in \operatorname{Ul}_I(R)$
, the pushout and pullback of
$M',N'\in \operatorname{Ul}_I(R)$
, the pushout and pullback of
![]() $\sigma $
by f and g in
$\sigma $
by f and g in
![]() ${\operatorname{mod}}\ R$
, respectively, are actually pushout and pullback in
${\operatorname{mod}}\ R$
, respectively, are actually pushout and pullback in
![]() ${\operatorname{mod}} (B(I))$
. Let us look at the pushout case, as the pullback case is similar. If we have the following pushout diagram:
${\operatorname{mod}} (B(I))$
. Let us look at the pushout case, as the pullback case is similar. If we have the following pushout diagram:

then in the bottom row, we again have
![]() $Y\in \operatorname{Ul}_I(R)$
, since
$Y\in \operatorname{Ul}_I(R)$
, since
![]() $\operatorname{Ul}_I(R)$
along with all its short exact sequences is an exact subcategory of
$\operatorname{Ul}_I(R)$
along with all its short exact sequences is an exact subcategory of
![]() ${\operatorname{mod}}\ R$
by Corollary 4.7. Hence, in the above diagram, all the modules are in
${\operatorname{mod}}\ R$
by Corollary 4.7. Hence, in the above diagram, all the modules are in
![]() $\operatorname{Ul}_I(R)=\operatorname{CM}(B(I))$
, so all the R-linear maps are moreover
$\operatorname{Ul}_I(R)=\operatorname{CM}(B(I))$
, so all the R-linear maps are moreover
![]() $B(I)$
-linear. Since
$B(I)$
-linear. Since
![]() $\operatorname{CM}(B(I))$
is an extension closed subcategory of
$\operatorname{CM}(B(I))$
is an extension closed subcategory of
![]() ${\operatorname{mod}}(B(I))$
, it is an exact subcategory of
${\operatorname{mod}}(B(I))$
, it is an exact subcategory of
![]() ${\operatorname{mod}} (B(I))$
by Proposition 3.5. Thus, this is a pushout diagram in
${\operatorname{mod}} (B(I))$
by Proposition 3.5. Thus, this is a pushout diagram in
![]() ${\operatorname{mod}}(B(I))$
as well by [Reference Bühler6, Prop. 2.12]. This is what we wanted to show.
${\operatorname{mod}}(B(I))$
as well by [Reference Bühler6, Prop. 2.12]. This is what we wanted to show.
Corollary 5.2.13. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
, and let I be an
$1$
, and let I be an
![]() $\mathfrak {m}$
-primary ideal of R. If
$\mathfrak {m}$
-primary ideal of R. If
![]() $M,N\in \operatorname{Ul}_I(R)$
are such that
$M,N\in \operatorname{Ul}_I(R)$
are such that
![]() ${\operatorname{Ext}}^1_{B(I)}(M,N)=0$
, then
${\operatorname{Ext}}^1_{B(I)}(M,N)=0$
, then
![]() $\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,N)=0$
.
$\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,N)=0$
.
In the following, for a module X over a ring R, by
![]() $\operatorname{add}_R(X)$
, we denote the collection of all R-modules Y such that there exist an R-module Z and an isomorphism of R-modules
$\operatorname{add}_R(X)$
, we denote the collection of all R-modules Y such that there exist an R-module Z and an isomorphism of R-modules
![]() $Y\oplus Z\cong X^{\oplus n}$
for some integer
$Y\oplus Z\cong X^{\oplus n}$
for some integer
![]() $n\ge 0$
.
$n\ge 0$
.
Theorem 5.2.14. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let I be an
$1$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal of R. Then the following hold:
$\mathfrak {m}$
-primary ideal of R. Then the following hold:
-
(1) If
 $M\in \operatorname{add}_R(B(I))$
, then
$M\in \operatorname{add}_R(B(I))$
, then
 $\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M, \operatorname{Ul}_I(R))=0$
.
$\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M, \operatorname{Ul}_I(R))=0$
. -
(2) Let
 $M\in \operatorname{Ul}(R)$
. Then
$M\in \operatorname{Ul}(R)$
. Then
 $M\in \operatorname{add}_R(B(\mathfrak {m}))$
if and only if
$M\in \operatorname{add}_R(B(\mathfrak {m}))$
if and only if
 $\mathfrak {m} {\operatorname{Ext}}^1_R(M, \operatorname{Ul}(R))=0$
.
$\mathfrak {m} {\operatorname{Ext}}^1_R(M, \operatorname{Ul}(R))=0$
. -
(3) If
 $B(I)$
is a Gorenstein ring, then
$B(I)$
is a Gorenstein ring, then
 $\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(\operatorname{Ul}_I(R),B(I))=0$
. The converse holds when
$\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(\operatorname{Ul}_I(R),B(I))=0$
. The converse holds when
 $I=\mathfrak {m}$
.
$I=\mathfrak {m}$
.
Proof. (1) Denote
![]() $S:=B(I)$
. If
$S:=B(I)$
. If
![]() $M\in \operatorname{add}_R(S)(\subseteq \operatorname{Ul}_I(R))$
, then there exist
$M\in \operatorname{add}_R(S)(\subseteq \operatorname{Ul}_I(R))$
, then there exist
![]() $X\in {\operatorname{mod}}(R)$
and an isomorphism of R-modules
$X\in {\operatorname{mod}}(R)$
and an isomorphism of R-modules
![]() $M\oplus X\cong B(I)^{\oplus n}$
for some
$M\oplus X\cong B(I)^{\oplus n}$
for some
![]() $n\ge 0$
. Then
$n\ge 0$
. Then
![]() $M,X$
are I-Ulrich, so
$M,X$
are I-Ulrich, so
![]() $M,X\in \operatorname{CM}(S)$
. Hence, the isomorphism is also S-linear by [Reference Leuschke and Wiegand27, Prop. 4.14(i)], so M is a projective S-module. Thus,
$M,X\in \operatorname{CM}(S)$
. Hence, the isomorphism is also S-linear by [Reference Leuschke and Wiegand27, Prop. 4.14(i)], so M is a projective S-module. Thus,
![]() ${\operatorname{Ext}}^1_S(M,N)=0$
for all
${\operatorname{Ext}}^1_S(M,N)=0$
for all
![]() $N\in \operatorname{CM}(S)=\operatorname{Ul}_I(R)$
. Now, the conclusion follows from Corollary 5.2.13.
$N\in \operatorname{CM}(S)=\operatorname{Ul}_I(R)$
. Now, the conclusion follows from Corollary 5.2.13.
(2) If
![]() $M\in \operatorname{add}_R(B(\mathfrak {m}))$
, then the conclusion follows by (1) as
$M\in \operatorname{add}_R(B(\mathfrak {m}))$
, then the conclusion follows by (1) as
![]() $\mathfrak {m}\subseteq \operatorname{tr}_R(\mathfrak {m})$
. So, assume
$\mathfrak {m}\subseteq \operatorname{tr}_R(\mathfrak {m})$
. So, assume
![]() $M\in \operatorname{Ul}(R)$
and
$M\in \operatorname{Ul}(R)$
and
![]() $\mathfrak {m} {\operatorname{Ext}}^1_R(M,N)=0$
for all
$\mathfrak {m} {\operatorname{Ext}}^1_R(M,N)=0$
for all
![]() $N\in \operatorname{Ul}(R)$
. By Proposition 5.2.6, we then have
$N\in \operatorname{Ul}(R)$
. By Proposition 5.2.6, we then have
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N)=0$
for all
${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,N)=0$
for all
![]() $N\in \operatorname{Ul}(R)$
. Now, denote
$N\in \operatorname{Ul}(R)$
. Now, denote
![]() $S=B(\mathfrak {m})$
. Then, by Lemma 5.2.12, we have
$S=B(\mathfrak {m})$
. Then, by Lemma 5.2.12, we have
![]() ${\operatorname{Ext}}^1_{S}(M,N)=0$
for all
${\operatorname{Ext}}^1_{S}(M,N)=0$
for all
![]() $N\in \operatorname{Ul}(R)=\operatorname{CM}(S)$
. We know that, for any Cohen–Macaulay ring S, and
$N\in \operatorname{Ul}(R)=\operatorname{CM}(S)$
. We know that, for any Cohen–Macaulay ring S, and
![]() $M\in \operatorname{CM}(S)$
, we have
$M\in \operatorname{CM}(S)$
, we have
![]() ${\operatorname{Ext}}^1_S(M,\operatorname{CM}(S))=0$
if and only if
${\operatorname{Ext}}^1_S(M,\operatorname{CM}(S))=0$
if and only if
![]() $M\in \operatorname{add}_S(S)$
. Indeed, one direction is clear since
$M\in \operatorname{add}_S(S)$
. Indeed, one direction is clear since
![]() $M\in \operatorname{add}_S(S)$
implies M is projective. For the converse, we notice that as M is finitely generated over S, so we have a short exact sequence
$M\in \operatorname{add}_S(S)$
implies M is projective. For the converse, we notice that as M is finitely generated over S, so we have a short exact sequence
![]() $\sigma : 0\to M'\to S^{\oplus n}\to M \to 0$
for some
$\sigma : 0\to M'\to S^{\oplus n}\to M \to 0$
for some
![]() $n>0$
and S-module
$n>0$
and S-module
![]() $M'$
. Moreover, S being Cohen–Macaulay implies
$M'$
. Moreover, S being Cohen–Macaulay implies
![]() $M'\in \operatorname{CM}(S)$
, and now the vanishing of
$M'\in \operatorname{CM}(S)$
, and now the vanishing of
![]() ${\operatorname{Ext}}^1_S(M,M')$
gives that the sequence
${\operatorname{Ext}}^1_S(M,M')$
gives that the sequence
![]() $\sigma $
splits. Hence,
$\sigma $
splits. Hence,
![]() $M\in \operatorname{add}_S(S)$
. Now, applying this observation to our scenario with
$M\in \operatorname{add}_S(S)$
. Now, applying this observation to our scenario with
![]() $S=B(\mathfrak {m})$
, we get
$S=B(\mathfrak {m})$
, we get
![]() $M\in \operatorname{add}_S(B(\mathfrak {m}))=\operatorname{add}_R(B(\mathfrak {m}))$
, where this last equality follows from the fact that direct summand of
$M\in \operatorname{add}_S(B(\mathfrak {m}))=\operatorname{add}_R(B(\mathfrak {m}))$
, where this last equality follows from the fact that direct summand of
![]() $B(\mathfrak {m})$
is in
$B(\mathfrak {m})$
is in
![]() $\operatorname{CM}(B(\mathfrak {m}))$
and consequently, R-linear maps are S-linear (see [Reference Leuschke and Wiegand27, Prop. 4.14(i)]).
$\operatorname{CM}(B(\mathfrak {m}))$
and consequently, R-linear maps are S-linear (see [Reference Leuschke and Wiegand27, Prop. 4.14(i)]).
(3) Nothing to prove if R is regular, so we assume R is singular. If
![]() $B(I)$
is a Gorenstein ring, then
$B(I)$
is a Gorenstein ring, then
![]() ${\operatorname{Ext}}^1_{B(I)}(M,B(I))=0$
for all
${\operatorname{Ext}}^1_{B(I)}(M,B(I))=0$
for all
![]() $M \in \operatorname{CM}(B(I))=\operatorname{Ul}_I(R)$
. Since
$M \in \operatorname{CM}(B(I))=\operatorname{Ul}_I(R)$
. Since
![]() $B(I)$
is I-Ulrich, by Lemma 5.2.12, we get
$B(I)$
is I-Ulrich, by Lemma 5.2.12, we get
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,B(I))=0$
for all
${\operatorname{Ext}}^1_{\operatorname{Ul}_I(R)}(M,B(I))=0$
for all
![]() $M \in \operatorname{Ul}_I(R)$
. Then, by Corollary 5.2.13, we get
$M \in \operatorname{Ul}_I(R)$
. Then, by Corollary 5.2.13, we get
![]() $\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,B(I))=0$
for all
$\operatorname{tr}_R(I){\operatorname{Ext}}^1_R(M,B(I))=0$
for all
![]() $M \in \operatorname{Ul}_I(R)$
. For the converse part, assume
$M \in \operatorname{Ul}_I(R)$
. For the converse part, assume
![]() $I=\mathfrak {m}$
and
$I=\mathfrak {m}$
and
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(M,B(\mathfrak {m}))=0$
for all
$\mathfrak {m}{\operatorname{Ext}}^1_R(M,B(\mathfrak {m}))=0$
for all
![]() $M \in \operatorname{Ul}(R)$
. Then, by Proposition 5.2.6, we have
$M \in \operatorname{Ul}(R)$
. Then, by Proposition 5.2.6, we have
![]() ${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,B(\mathfrak {m}))=0$
for all
${\operatorname{Ext}}^1_{\operatorname{Ul}(R)}(M,B(\mathfrak {m}))=0$
for all
![]() $M\in \operatorname{Ul}(R)$
. Hence, by Lemma 5.2.12, we have
$M\in \operatorname{Ul}(R)$
. Hence, by Lemma 5.2.12, we have
![]() ${\operatorname{Ext}}^1_{B(\mathfrak {m})}(M,B(\mathfrak {m}))=0$
for all
${\operatorname{Ext}}^1_{B(\mathfrak {m})}(M,B(\mathfrak {m}))=0$
for all
![]() $M\in \operatorname{Ul}(R)=\operatorname{CM}(B(\mathfrak {m}))$
. Now, we note that for a finite-dimensional Cohen–Macaulay ring S,
$M\in \operatorname{Ul}(R)=\operatorname{CM}(B(\mathfrak {m}))$
. Now, we note that for a finite-dimensional Cohen–Macaulay ring S,
![]() ${\operatorname{Ext}}^1_S(M,S)=0$
for all
${\operatorname{Ext}}^1_S(M,S)=0$
for all
![]() $M \in \operatorname{CM}(S)$
if and only if S is Gorenstein. Indeed, if S is Gorenstein, then the vanishing is clear by [Reference Bruns and Herzog3, Def. 3.1.18 and Props. 3.1.9 and 3.1.24]. Conversely, let
$M \in \operatorname{CM}(S)$
if and only if S is Gorenstein. Indeed, if S is Gorenstein, then the vanishing is clear by [Reference Bruns and Herzog3, Def. 3.1.18 and Props. 3.1.9 and 3.1.24]. Conversely, let
![]() $d=\dim S$
. Then, for every
$d=\dim S$
. Then, for every
![]() $\mathfrak {p} \in \operatorname{Spec}(S)$
, we have
$\mathfrak {p} \in \operatorname{Spec}(S)$
, we have
![]() $\Omega ^d_S(S/\mathfrak {p}) \in \operatorname{CM}(S)$
(by localizing and applying depth lemma). So, now the vanishing of
$\Omega ^d_S(S/\mathfrak {p}) \in \operatorname{CM}(S)$
(by localizing and applying depth lemma). So, now the vanishing of
![]() ${\operatorname{Ext}}^{d+1}_S(S/\mathfrak {p}, S)\cong {\operatorname{Ext}}^1_S(\Omega ^d_S(S/\mathfrak {p}),S)$
for every
${\operatorname{Ext}}^{d+1}_S(S/\mathfrak {p}, S)\cong {\operatorname{Ext}}^1_S(\Omega ^d_S(S/\mathfrak {p}),S)$
for every
![]() $\mathfrak {p}\in \operatorname{Spec}(S)$
implies
$\mathfrak {p}\in \operatorname{Spec}(S)$
implies
![]() $\operatorname{inj dim}_S S <\infty $
. Thus, S is Gorenstein by [Reference Bruns and Herzog3, Def. 3.1.18 and Prop. 3.1.9]. Now, applying this observation to our scenario with
$\operatorname{inj dim}_S S <\infty $
. Thus, S is Gorenstein by [Reference Bruns and Herzog3, Def. 3.1.18 and Prop. 3.1.9]. Now, applying this observation to our scenario with
![]() $S=B(\mathfrak {m})$
, we get that
$S=B(\mathfrak {m})$
, we get that
![]() $B(\mathfrak {m})$
is Gorenstein.
$B(\mathfrak {m})$
is Gorenstein.
Since for one-dimensional local Cohen–Macaulay rings
![]() $(R,\mathfrak {m})$
of minimal multiplicity it holds that
$(R,\mathfrak {m})$
of minimal multiplicity it holds that
![]() $B(\mathfrak {m})=(\mathfrak {m}:\mathfrak {m})\cong \mathfrak {m}$
, the following corollary is an immediate consequence of Theorem 5.2.14(3) and [Reference Goto, Matsuoka and Phuong20, Th. 5.1].
$B(\mathfrak {m})=(\mathfrak {m}:\mathfrak {m})\cong \mathfrak {m}$
, the following corollary is an immediate consequence of Theorem 5.2.14(3) and [Reference Goto, Matsuoka and Phuong20, Th. 5.1].
Corollary 5.2.15. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
and minimal multiplicity. Then, R is almost Gorenstein if and only if
$1$
and minimal multiplicity. Then, R is almost Gorenstein if and only if
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})=0$
.
$\mathfrak {m}{\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})=0$
.
Finally, we give one more application of Theorem 5.2.14(3), for which we first record an easy observation.
Lemma 5.2.16. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
. Let I be an
$1$
. Let I be an
![]() $\mathfrak {m}$
-primary ideal of R admitting a principal reduction
$\mathfrak {m}$
-primary ideal of R admitting a principal reduction
![]() $x\in I$
. Then,
$x\in I$
. Then,
![]() $\mathfrak {m}$
is I-Ulrich if and only if
$\mathfrak {m}$
is I-Ulrich if and only if
![]() $\mathfrak {m}\subseteq ((x):I)$
.
$\mathfrak {m}\subseteq ((x):I)$
.
Proof. If I is principal, then all MCM modules are I-Ulrich. So, it is enough to assume I is not principal. If
![]() $\mathfrak {m}$
is I-Ulrich, then
$\mathfrak {m}$
is I-Ulrich, then
![]() $I\mathfrak {m} =x\mathfrak {m}$
(see [Reference Dao, Maitra and Sridhar11, Prop. 4.5]). So,
$I\mathfrak {m} =x\mathfrak {m}$
(see [Reference Dao, Maitra and Sridhar11, Prop. 4.5]). So,
![]() $\mathfrak {m} \subseteq ((x):I)$
. Conversely, let
$\mathfrak {m} \subseteq ((x):I)$
. Conversely, let
![]() $\mathfrak {m}\subseteq ((x):I)$
. Then,
$\mathfrak {m}\subseteq ((x):I)$
. Then,
![]() $\mathfrak {m}\subseteq ((x):_RI)$
. We claim that
$\mathfrak {m}\subseteq ((x):_RI)$
. We claim that
![]() $x\notin \mathfrak {m} I$
. Since
$x\notin \mathfrak {m} I$
. Since
![]() $x\in I$
is a principal reduction of I, we have
$x\in I$
is a principal reduction of I, we have
![]() $I^{n+1}=xI^n$
for some
$I^{n+1}=xI^n$
for some
![]() $n\ge 1$
. Hence, if
$n\ge 1$
. Hence, if
![]() $x\in \mathfrak {m} I$
, then
$x\in \mathfrak {m} I$
, then
![]() $I^{n+1}\subseteq \mathfrak {m} I^{n+1}$
. So,
$I^{n+1}\subseteq \mathfrak {m} I^{n+1}$
. So,
![]() $I^{n+1}=\mathfrak {m} I^{n+1}$
. Hence, by Nakayama’s lemma,
$I^{n+1}=\mathfrak {m} I^{n+1}$
. Hence, by Nakayama’s lemma,
![]() $I^{n+1}=0$
, contradicting I is
$I^{n+1}=0$
, contradicting I is
![]() $\mathfrak {m}$
-primary. Thus,
$\mathfrak {m}$
-primary. Thus,
![]() $x\in I\setminus \mathfrak {m} I$
. Since
$x\in I\setminus \mathfrak {m} I$
. Since
![]() $\mathfrak {m}\subseteq ((x):_R I)$
and I is not principal, we have
$\mathfrak {m}\subseteq ((x):_R I)$
and I is not principal, we have
![]() $\mathfrak {m} \subseteq (x\mathfrak {m} :_R I)$
by Lemma 5.1.7. So,
$\mathfrak {m} \subseteq (x\mathfrak {m} :_R I)$
by Lemma 5.1.7. So,
![]() $\mathfrak {m} I \subseteq x \mathfrak {m}$
. Hence,
$\mathfrak {m} I \subseteq x \mathfrak {m}$
. Hence,
![]() $\mathfrak {m} I=x\mathfrak {m}$
, so
$\mathfrak {m} I=x\mathfrak {m}$
, so
![]() $\mathfrak {m}$
is I-Ulrich.
$\mathfrak {m}$
is I-Ulrich.
Corollary 5.2.17. Let
![]() $(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
$(R,\mathfrak {m})$
be a local Cohen–Macaulay ring of dimension
![]() $1$
, with infinite residue field, and minimal multiplicity, admitting a canonical module. If
$1$
, with infinite residue field, and minimal multiplicity, admitting a canonical module. If
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})=0$
, then R admits a canonical ideal
$\mathfrak {m}{\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})=0$
, then R admits a canonical ideal
![]() $\omega $
and
$\omega $
and
![]() $B(\omega )$
is Gorenstein. Consequently,
$B(\omega )$
is Gorenstein. Consequently,
![]() $\mathfrak {m}{\operatorname{Ext}}^1_{R}(\operatorname{Ul}_{\omega }(R),B(\omega ))=0$
.
$\mathfrak {m}{\operatorname{Ext}}^1_{R}(\operatorname{Ul}_{\omega }(R),B(\omega ))=0$
.
Proof. Let
![]() $\omega $
be a canonical module of R. We show that
$\omega $
be a canonical module of R. We show that
![]() $\omega $
can be identified with an ideal of R,
$\omega $
can be identified with an ideal of R,
![]() $\mathfrak {m}\subseteq \operatorname{tr}_R(\omega )$
, and
$\mathfrak {m}\subseteq \operatorname{tr}_R(\omega )$
, and
![]() $B(\omega )$
is Gorenstein. Since R has minimal multiplicity and
$B(\omega )$
is Gorenstein. Since R has minimal multiplicity and
![]() $\mathfrak {m}{\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})=0$
, R is almost Gorenstein by Corollary 5.2.15. Hence,
$\mathfrak {m}{\operatorname{Ext}}^1_R(\operatorname{Ul}(R),\mathfrak {m})=0$
, R is almost Gorenstein by Corollary 5.2.15. Hence,
![]() $\mathfrak {m}\subseteq \operatorname{tr}_R(\omega )$
from [Reference Herzog, Hibi and Stamate22, Def. 2.2 and Prop. 6.1], so R is generically Gorenstein (see [Reference Herzog, Hibi and Stamate22, Lem. 2.1]). Hence,
$\mathfrak {m}\subseteq \operatorname{tr}_R(\omega )$
from [Reference Herzog, Hibi and Stamate22, Def. 2.2 and Prop. 6.1], so R is generically Gorenstein (see [Reference Herzog, Hibi and Stamate22, Lem. 2.1]). Hence,
![]() $\omega $
can be identified with an ideal of R by [Reference Bruns and Herzog3, Prop. 3.3.18]. Since R is almost Gorenstein, we have
$\omega $
can be identified with an ideal of R by [Reference Bruns and Herzog3, Prop. 3.3.18]. Since R is almost Gorenstein, we have
![]() $\mathfrak {m} \subseteq ((x):\omega )$
for some principal reduction x of
$\mathfrak {m} \subseteq ((x):\omega )$
for some principal reduction x of
![]() $\omega $
(see [Reference Goto, Matsuoka and Phuong20, Setting 3.4 and Th. 3.11]). Thus,
$\omega $
(see [Reference Goto, Matsuoka and Phuong20, Setting 3.4 and Th. 3.11]). Thus,
![]() $\mathfrak {m}$
is
$\mathfrak {m}$
is
![]() $\omega $
-Ulrich by Lemma 5.2.16. So,
$\omega $
-Ulrich by Lemma 5.2.16. So,
![]() $\mathfrak {m} \in \operatorname{CM}(B(\omega ))$
by [Reference Dao, Maitra and Sridhar11, Th. 4.6]. Hence,
$\mathfrak {m} \in \operatorname{CM}(B(\omega ))$
by [Reference Dao, Maitra and Sridhar11, Th. 4.6]. Hence,
![]() $\mathfrak {m}\subseteq \operatorname{tr}_R(\mathfrak {m}) \subseteq (R:_{Q(R)}B(\omega ))$
by [Reference Dao, Maitra and Sridhar11, Th. 2.9]. Thus, the conductor
$\mathfrak {m}\subseteq \operatorname{tr}_R(\mathfrak {m}) \subseteq (R:_{Q(R)}B(\omega ))$
by [Reference Dao, Maitra and Sridhar11, Th. 2.9]. Thus, the conductor
![]() $c_R(B(\omega )):=(R:_{Q(R)}B(\omega ))$
of
$c_R(B(\omega )):=(R:_{Q(R)}B(\omega ))$
of
![]() $B(\omega )$
is either
$B(\omega )$
is either
![]() $\mathfrak {m}$
or R. As R has minimal multiplicity, by using [Reference Bruns and Herzog3, Exercise 4.6.14(c)], we see that
$\mathfrak {m}$
or R. As R has minimal multiplicity, by using [Reference Bruns and Herzog3, Exercise 4.6.14(c)], we see that
![]() $c_R(B(\omega ))$
satisfies the condition (2) of [Reference Goto, Matsuoka and Phuong20, Cor. 3.8]. Thus,
$c_R(B(\omega ))$
satisfies the condition (2) of [Reference Goto, Matsuoka and Phuong20, Cor. 3.8]. Thus,
![]() $B(\omega )$
is Gorenstein by [Reference Goto, Matsuoka and Phuong20, Cor. 3.8]. Now, the claim follows from Theorem 5.2.14(3).
$B(\omega )$
is Gorenstein by [Reference Goto, Matsuoka and Phuong20, Cor. 3.8]. Now, the claim follows from Theorem 5.2.14(3).
Acknowledgments
We thank David Eisenbud for helpful conversations and for pointing out reference [Reference Eisenbud and Schreyer15]. We also thank the anonymous referee for numerous helpful suggestions that improved the exposition of the paper.