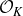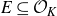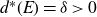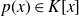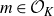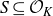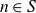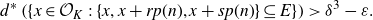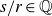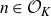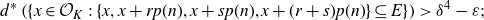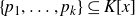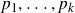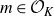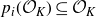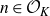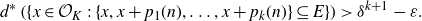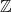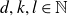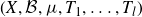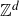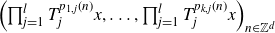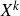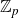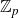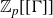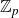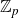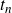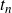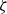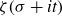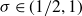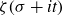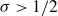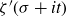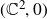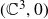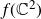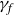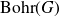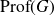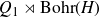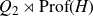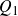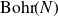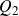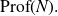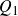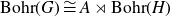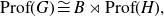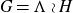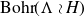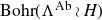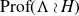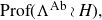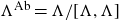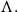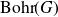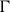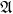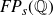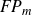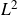Research Article
Multiple recurrence and popular differences for polynomial patterns in rings of integers
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2023, pp. 239-278
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some torsion-free solvable groups with few subquotients
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2023, pp. 279-286
-
- Article
-
- You have access
- HTML
- Export citation
Structure of fine Selmer groups over
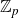 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2023, pp. 287-308
-
- Article
-
- You have access
- HTML
- Export citation
A problem of Erdős–Graham–Granville–Selfridge on integral points on hyperelliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2023, pp. 309-323
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spirals of Riemann’s Zeta-Function — Curvature, Denseness and Universality
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2023, pp. 325-338
-
- Article
-
- You have access
- HTML
- Export citation
On the topology of the transversal slice of a quasi-homogeneous map germ
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2023, pp. 339-359
-
- Article
-
- You have access
- HTML
- Export citation
Nonvarying, affine and extremal geometry of strata of differentials
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2023, pp. 361-371
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Bohr compactifications and profinite completions of group extensions
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2023, pp. 373-393
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian tropical covers
- Part of:
-
- Published online by Cambridge University Press:
- 10 October 2023, pp. 395-416
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On subdirect products of type FPn of limit groups over Droms RAAGs
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2023, pp. 417-440
-
- Article
-
- You have access
- HTML
- Export citation
Three Schur functors related to pre-Lie algebras
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2023, pp. 441-458
-
- Article
-
- You have access
- HTML
- Export citation
Zeros, chaotic ratios and the computational complexity of approximating the independence polynomial
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2023, pp. 459-494
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 176 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 16 February 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 176 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 16 February 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation