Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-03T08:33:23.975Z Has data issue: false hasContentIssue false
  • English
  • Français

On tau-tilting subcategories

Part of: Homological methods Homological algebra Abelian categories Rings and algebras arising under various constructions

Published online by Cambridge University Press:  08 March 2024

Javad Asadollahi Open the ORCID record for Javad Asadollahi [Opens in a new window] ,
Somayeh Sadeghi  and
Hipolito Treffinger
Javad Asadollahi*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Statistics, University of Isfahan, 81746-73441 Isfahan, Iran e-mail: [email protected]
Somayeh Sadeghi
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), 19395-5746 Tehran, Iran e-mail: [email protected]
Hipolito Treffinger
Affiliation:
Instituto de Investigaciones Matemáticas, Luis A. Santaló, UBA-CONICET, C1428 Buenos Aires, Argentina e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The main theme of this paper is to study 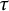$\tau $-tilting subcategories in an abelian category 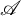$\mathscr {A}$ with enough projective objects. We introduce the notion of 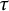$\tau $-cotorsion torsion triples and investigate a bijection between the collection of 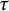$\tau $-cotorsion torsion triples in 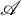$\mathscr {A}$ and the collection of support 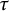$\tau $-tilting subcategories of 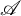$\mathscr {A}$, generalizing the bijection by Bauer, Botnan, Oppermann, and Steen between the collection of cotorsion torsion triples and the collection of tilting subcategories of 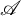$\mathscr {A}$. General definitions and results are exemplified using persistent modules. If 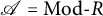$\mathscr {A}=\mathrm{Mod}\mbox {-}R$, where R is a unitary associative ring, we characterize all support 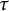$\tau $-tilting (resp. all support 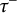$\tau ^-$-tilting) subcategories of 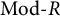$\mathrm{Mod}\mbox {-}R$ in terms of finendo quasitilting (resp. quasicotilting) modules. As a result, it will be shown that every silting module (resp. every cosilting module) induces a support 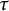$\tau $-tilting (resp. support 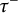$\tau ^{-}$-tilting) subcategory of 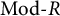$\mathrm{Mod}\mbox {-}R$. We also study the theory in 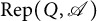$\mathrm {Rep}(Q, \mathscr {A})$, where Q is a finite and acyclic quiver. In particular, we give an algorithm to construct support 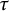$\tau $-tilting subcategories in 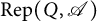$\mathrm {Rep}(Q, \mathscr {A})$ from certain support 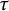$\tau $-tilting subcategories of 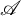$\mathscr {A}$.

Keywords

Abelian category(τ-)tilting subcategorytorsion theorysilting modulequiver representation

MSC classification

Primary: 18E10: Exact categories, abelian categories 18E40: Torsion theories, radicals 16S90: Torsion theories; radicals on module categories
Secondary: 16E30: Homological functors on modules (Tor, Ext, etc.) 18G15: Ext and Tor, generalizations, Künneth formula
Type
Article
Information
Canadian Journal of Mathematics , Volume 77 , Issue 3 , June 2025 , pp. 975 - 1012
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The work of the first author is based on research funded by the Iran National Science Foundation (INSF) under Project No. 4001480. The research of the second author is supported by a grant from IPM. The third author is supported by the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreement No. 893654.

References

Adachi, T., Iyama, O., and Reiten, I., $\tau$ -tilting theory. Compos. Math. 150(2014), no. 3, 415–452.CrossRefGoogle Scholar
Angeleri Hügel, L., Marks, F., and Vitória, J., Silting modules. Int. Math. Res. Not. IMRN 4(2016), 1251–1284.CrossRefGoogle Scholar
Angeleri Hügel, L., Tonolo, A., and Trlifaj, J., Tilting preenvelopes and cotilting precovers. Algebr. Represent. Theory 4(2001), no. 2, 155–170.CrossRefGoogle Scholar
Assem, I., Simson, D., and Skowronski, A., Elements of the representation theory of associative algebras I: techniques of representation theory, London Mathematical Society Student Texts, 65, Cambridge University Press, Cambridge, 2006.CrossRefGoogle Scholar
Auslander, M., Platzeck, M. I., and Reiten, I., Coxeter functors without diagrams. Trans. Amer. Math. Soc. 250(1979), 1–46.CrossRefGoogle Scholar
Auslander, M. and Smalø, S. O., Almost split sequences in subcategories. J. Algebra 69(1981), 426–454. Addendum: J. Algebra 71(1981), 592–594.CrossRefGoogle Scholar
Bauer, U., Botnan, M. B., Oppermann, S., and Steen, J., Cotorsion torsion triples and the representation theory of filtered hierarchical clustering. Adv. Math. 369(2020), 107171.CrossRefGoogle Scholar
Beligiannis, A., On the Freyd categories of an additive category. Homology Homotopy Appl. 2(2000), 147–185.CrossRefGoogle Scholar
Beligiannis, A., Homotopy theory of modules and Gorenstein rings. Math. Scand. 89(2001), 5–45.CrossRefGoogle Scholar
Beligiannis, A., Tilting theory in abelian categories and related homological and homotopical structures. Unpublished manuscript, 2010.Google Scholar
Beligiannis, A. and Reiten, I., Homological and homotopical aspects of torsion theories. Mem. Amer. Math. Soc. 188(2007), no. 883, viii + 207.Google Scholar
Bernstein, I. N., Gelfand, I. M., and Ponomarev, V. A., Coxeter functors, and Gabriel’s theorem. Uspehi Mat. Nauk. 28(1973), no. 2(170), 19–33.Google Scholar
Bongartz, K., Tilted algebras . In: Representations of algebras. Lecture Notes in Mathematics, 903, Springer, Berlin, 1980, pp. 26–38.Google Scholar
Breaz, S. and Pop, F., Cosilting modules. Algebr. Represent. Theory 20(2017), 1305–1321.CrossRefGoogle Scholar
Brenner, S. and Butler, M. C. R., Generalizations of the Bernstein–Gelfand–Ponomarev reflection functors . In: Representation theory, II (proc. second internat. conf., Carleton Univ., Ottawa, Ont., 1979), Lecture Notes in Mathematics, 832, Springer, Berlin–New York, 1980, pp. 103–169.Google Scholar
Buan, A. B. and Zhou, Y., Weak cotorsion, $\tau$ -tilting and two-term categories. J. Pure Appl. Algebra 228(2024), 107445.CrossRefGoogle Scholar
Carlsson, G., Topology and data. Bull. Amer. Math. Soc. (N.S.) 46(2009), no. 2, 255–308.CrossRefGoogle Scholar
Crawley-Boevey, W., Decomposition of pointwise finite-dimensional persistence modules. J. Algebra Appl. 14(2015), no. 5, 1550066.CrossRefGoogle Scholar
Dickson, S. E., A torsion theory for abelian categories. Trans. Amer. Math. Soc. 121(1966), 223–235.CrossRefGoogle Scholar
Enochs, E. and Estrada, S., Projective representations of quivers. Comm. Algebra 33(2005), 3467–3478.CrossRefGoogle Scholar
Enochs, E., Estrada, S., and Rozas, J. R. G., Injective representations of infinite quivers. Applications. Canad. J. Math. 61(2009), 315–335.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations. J. Amer. Math. Soc. 15(2002), no. 2, 497–529.CrossRefGoogle Scholar
Happel, D. and Ringel, C. M., Tilted algebras. Trans. Amer. Math. Soc. 274(1982), no. 2, 399–443.CrossRefGoogle Scholar
Happel, D. and Unger, L., Almost complete tilting modules. Proc. Amer. Math. Soc. 107(1989), no. 3, 603–610.CrossRefGoogle Scholar
Holm, H. and Jørgensen, P., Cotorsion pairs in categories of quiver representations. Kyoto J. Math. 59(2019), no. 3, 575–606.CrossRefGoogle Scholar
Iyama, O., Jørgensen, P., and Yang, D., Intermediate co-t-structures, two-term silting objects, $\tau$ -tilting modules, and torsion classes. Algebra Number Theory 8(2014), no. 10, 2413–2431.CrossRefGoogle Scholar
Jasso, G., Reduction of $\tau$ -tilting modules and torsion pairs. Int. Math. Res. Not. IMRN 16(2015), 7190–7237.CrossRefGoogle Scholar
Liu, Y. and Zhou, P., $\tau$ -tilting theory in abelian categories. Proc. Amer. Math. Soc. 398(2014), 63–110.Google Scholar
Oudot, S. Y., Persistence theory: from quiver representations to data analysis, Mathematical Surveys and Monographs, 209, American Mathematical Society, Providence, RI, 2015.CrossRefGoogle Scholar
Rundsveen, E. S., Torsion, cotorsion and tilting in abelian categories, Master’s thesis in mathematical sciences, NTNU, 2021.Google Scholar
Salce, L., Cotorsion theories for abelian groups . In: Symposia mathematica. Vol. XXIII, conf. abelian groups and their relationship to the theory of modules, INDAM, Rome, 1977, pp. 11–32; Academic Press, London–New York, 1979.Google Scholar
Smalø, S. O., Torsion theories and tilting modules. Bull. Lond. Math. Soc. 16(1984), no. 5, 518–522.CrossRefGoogle Scholar
Treffinger, H., $\tau$ -tilting theory – an introduction, to appear in the Proceedings of the LMS Autumn Algebra School, 2020, arXiv:2106.00426v3.Google Scholar
Zhang, P. and Wei, J., Cosilting complexes and AIR-cotilting modules. J. Algebra 491(2017), 1–31.CrossRefGoogle Scholar
Zhang, P. and Wei, J., Quasi-cotilting modules and torsion-free classes. J. Algebra Appl. 18(2019), 1950214.CrossRefGoogle Scholar
Zhang, X., Self-orthogonal $\tau$ -tilting modules and tilting modules. J. Pure Appl. Algebra 226(2022), 106860.CrossRefGoogle Scholar