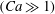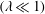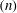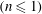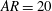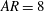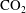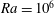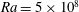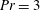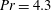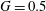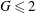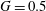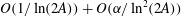JFM Papers
Hypersonic compression corner flow with large separated regions
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 471-494
-
- Article
- Export citation
Phase transitions on partially contaminated surface under the influence of thermocapillary flow
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 495-533
-
- Article
- Export citation
Low-order modelling of wake meandering behind turbines
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 534-560
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Newtonian slender drops in a nonlinear extensional flow
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 561-581
-
- Article
- Export citation
Flow physics and dynamics of flow-induced pitch oscillations of an airfoil
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 582-613
-
- Article
- Export citation
Effect of wing mass on the free flight of a butterfly-like model using immersed boundary–lattice Boltzmann simulations
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 614-647
-
- Article
- Export citation
The combined hydrodynamic and thermodynamic effects of immobilized proteins on the diffusion of mobile transmembrane proteins
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 648-681
-
- Article
- Export citation
On the shape of resolvent modes in wall-bounded turbulence
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 682-716
-
- Article
- Export citation
Flows over surface-mounted bluff bodies with different spanwise widths submerged in a deep turbulent boundary layer
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 717-758
-
- Article
- Export citation
Diffusive instabilities and spatial patterning from the coupling of reaction–diffusion processes with Stokes flow in complex domains
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 759-823
-
- Article
- Export citation
Lagrangian coherent structures and entrainment near the turbulent/non-turbulent interface of a gravity current
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 824-843
-
- Article
- Export citation
Robust low-dimensional modelling of falling liquid films subject to variable wall heating
-
- Published online by Cambridge University Press:
- 27 August 2019, pp. 844-881
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-similar dynamics of two-phase flows injected into a confined porous layer
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 882-921
-
- Article
- Export citation
Cessation and reversals of large-scale structures in square Rayleigh–Bénard cells
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 922-954
-
- Article
- Export citation
Oscillatory flow regimes around four cylinders in a diamond arrangement
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 955-1006
-
- Article
- Export citation
Analytical models of the wall-pressure spectrum under a turbulent boundary layer with adverse pressure gradient
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 1007-1062
-
- Article
- Export citation
Numerical investigation of controlling interfacial instabilities in non-standard Hele-Shaw configurations
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 1063-1097
-
- Article
- Export citation
Slender body theory for particles with non-circular cross-sections with application to particle dynamics in shear flows
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 1098-1133
-
- Article
- Export citation
Extension of classical stability theory to viscous planar wall-bounded shear flows
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 1134-1162
-
- Article
- Export citation
Stability of a temporally evolving natural convection boundary layer on an isothermal wall
-
- Published online by Cambridge University Press:
- 02 September 2019, pp. 1163-1185
-
- Article
- Export citation