Article contents
Oscillatory flow regimes around four cylinders in a diamond arrangement
Published online by Cambridge University Press: 02 September 2019
Abstract
Oscillatory flow around a cluster of four circular cylinders in a diamond arrangement is investigated using two-dimensional direct numerical simulation over Keulegan–Carpenter numbers (KC) ranging from 4 to 12 and Reynolds numbers (Re) from 40 to 230 at four gap-to-diameter ratios (G) of 0.5, 1, 2 and 4. Three types of flows, namely synchronous, quasi-periodic and desynchronized flows (along with 14 flow regimes) are mapped out in the (G, KC, Re)-parameter space. The observed flow characteristics around four cylinders in a diamond arrangement show a few unique features that are absent in the flow around four cylinders in a square arrangement reported by Tong et al. (J. Fluid Mech., vol. 769, 2015, pp. 298–336). These include (i) the dominance of flow around the cluster-scale structure at 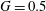 $G=0.5$ and 1, (ii) a substantial reduction of regime D flows in the regime maps, (iii) new quasi-periodic (phase trapping)
$G=0.5$ and 1, (ii) a substantial reduction of regime D flows in the regime maps, (iii) new quasi-periodic (phase trapping) 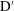 $\text{D}^{\prime }$ (at
$\text{D}^{\prime }$ (at 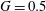 $G=0.5$ and 1) and period-doubling
$G=0.5$ and 1) and period-doubling 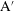 $\text{A}^{\prime }$ flows (at
$\text{A}^{\prime }$ flows (at 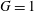 $G=1$) and most noteworthily (iv) abnormal behaviours at (
$G=1$) and most noteworthily (iv) abnormal behaviours at (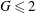 $G\leqslant 2$) (referred to as holes hereafter) such as the appearance of spatio-temporal synchronized flows in an area surrounded by a single type of synchronized flow in the regime map (
$G\leqslant 2$) (referred to as holes hereafter) such as the appearance of spatio-temporal synchronized flows in an area surrounded by a single type of synchronized flow in the regime map (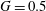 $G=0.5$). The mode competition between the cluster-scale and cylinder-scale flows is identified as the key flow mechanism responsible for those unique flow features, with the support of evidence derived from quantitative analysis. Phase dynamics is introduced for the first time in bluff-body flows, to the best knowledge of the authors, to quantitatively interpret the flow response (e.g. quasi-periodic flow features) around the cluster. It is instrumental in revealing the nature of regime
$G=0.5$). The mode competition between the cluster-scale and cylinder-scale flows is identified as the key flow mechanism responsible for those unique flow features, with the support of evidence derived from quantitative analysis. Phase dynamics is introduced for the first time in bluff-body flows, to the best knowledge of the authors, to quantitatively interpret the flow response (e.g. quasi-periodic flow features) around the cluster. It is instrumental in revealing the nature of regime 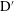 $\text{D}^{\prime }$ flows where the cluster-scale flow features are largely synchronized with the forcing of incoming oscillatory flow (phase trapping) but are modulated by localized flow features.
$\text{D}^{\prime }$ flows where the cluster-scale flow features are largely synchronized with the forcing of incoming oscillatory flow (phase trapping) but are modulated by localized flow features.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Ren et al. supplementary movie 1
Evolutions of streaklines for a typical regime F′ flow at (G, KC, Re) = (2, 8, 120).
Ren et al. supplementary movie 2
Evolutions of streaklines for a typical regime C′ flow at (G, KC, Re) = (1, 11, 110).
Ren et al. supplementary movie 3
Evolutions of streaklines for a typical regime A′ flow at (G, KC, Re) = (1, 6, 180).
Ren et al. supplementary movie 4
Evolutions of streaklines for a typical regime D1′ flow at (G, KC, Re) = (2, 11, 80).
Ren et al. supplementary movie 5
Evolutions of streaklines for a typical regime D2′ flow at (G, KC, Re) = (2, 11, 90).
Ren et al. supplementary movie 6
Evolutions of streaklines for a typical regime D3′ flow at (G, KC, Re) = (2, 10, 100).
- 14
- Cited by


