Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-09T23:56:46.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Newtonian slender drops in a nonlinear extensional flow

Published online by Cambridge University Press:  27 August 2019

Moshe Favelukis Open the ORCID record for Moshe Favelukis [Opens in a new window]
Moshe Favelukis*
Affiliation:
Department of Chemical Engineering, Shenkar – College of Engineering and Design, Ramat-Gan, 5252626, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this theoretical report we explore the deformation and stability of a power-law non-Newtonian slender drop embedded in a Newtonian liquid undergoing a nonlinear extensional creeping flow. The dimensionless parameters describing this problem are: the capillary number 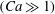$(Ca\gg 1)$, the viscosity ratio 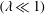$(\unicode[STIX]{x1D706}\ll 1)$, the power-law index 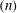$(n)$ and the nonlinear intensity of the flow $(|E|\ll 1)$. Asymptotic analytical solutions were obtained near the centre and close to the end of the drop suggesting that only Newtonian and shear thinning drops 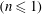$(n\leqslant 1)$ with pointed ends are possible. We described the shape of the drop as a series expansion about the centre of the drop, and performed a stability analysis in order to distinguish between stable and unstable stationary states and to establish the breakup point. Our findings suggest: (i) shear thinning drops are less elongated than Newtonian drops, (ii) as non-Newtonian effects increase or as $n$ decreases, breakup becomes more difficult, and (iii) as the flow becomes more nonlinear, breakup is facilitated.

JFM classification

Low-Reynolds-number flows: Slender-body theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 561 - 581
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Lo, T. S. 1978 Deformation and breakup of a single slender drop in an extensional flow. J. Fluid. Mech. 86, 641–672.10.1017/S0022112078001329Google Scholar
Antanovskii, L. K. 1996 Formation of a pointed drop in Taylor’s four-roller mill. J. Fluid. Mech. 327, 325–341.10.1017/S0022112096008567Google Scholar
Bentley, B. J. & Leal, L. G. 1986 An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech. 167, 241–283.10.1017/S0022112086002811Google Scholar
Booty, M. R. & Siegel, M. 2005 Steady deformation and tip-streaming of a slender bubble with surfactant in an extensional flow. J. Fluid Mech. 544, 243–275.10.1017/S0022112005006622Google Scholar
Brady, J. F. & Acrivos, A. 1982 The deformation and breakup of a slender drop in an extensional flow: inertial effects. J. Fluid Mech. 115, 443–451.10.1017/S0022112082000846Google Scholar
Briscoe, B. J., Lawrence, C. J. & Mietus, W. G. P. 1999 A review of immiscible fluid mixing. Adv. Colloid. Interface Sci. 81, 1–17.10.1016/S0001-8686(99)00002-0Google Scholar
Buckmaster, J. D. 1972 Pointed bubbles in slow viscous flow. J. Fluid. Mech. 55, 385–400.10.1017/S0022112072001910Google Scholar
Buckmaster, J. D. 1973 The bursting of pointed drops in slow viscous flow. Trans ASME J. Appl. Mech. E 40, 18–24.10.1115/1.3422923Google Scholar
Chhabra, R. P. 2006 Bubbles, Drops, and Particles in Non-Newtonian Fluids, 2nd edn. CRC Press.10.1201/9781420015386Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Delaby, I., Ernst, B., Germain, Y. & Muller, R. 1994 Droplet deformation in polymer blends during uniaxial elongational flow: influence of viscosity ratio for large Capillary numbers. J. Rheol. 38, 1705–1720.10.1122/1.550568Google Scholar
Favelukis, M. 2016 A slender drop in a nonlinear extensional flow. J. Fluid Mech. 808, 337–361.10.1017/jfm.2016.646Google Scholar
Favelukis, M. & Nir, A. 2001 Deformation of a slender bubble in a non-Newtonian liquid in an extensional flow. Chem. Engng Sci. 56, 4643–4648.10.1016/S0009-2509(01)00125-7Google Scholar
Favelukis, M., Lavrenteva, O. M. & Nir, A. 2005 Deformation and breakup of a non-Newtonian slender drop in an extensional flow. J. Non-Newtonian Fluid Mech. 125, 49–59.10.1016/j.jnnfm.2004.09.006Google Scholar
Favelukis, M., Lavrenteva, O. M. & Nir, A. 2006 Deformation and breakup of a non-Newtonian slender drop in an extensional flow: inertial effects and stability. J. Fluid Mech. 563, 133–158.10.1017/S0022112006001042Google Scholar
Favelukis, M., Lavrenteva, O. M. & Nir, A. 2012 On the evolution and breakup of slender drops in an extensional flow. Phys. Fluids 24, 043101.10.1063/1.3701373Google Scholar
Han, C. D. & Funatsu, K. 1978 An experimental study of droplet deformation and breakup in pressure-driven flows through converging and uniform channels. J. Rheol. 22, 113–133.10.1122/1.549475Google Scholar
Hinch, E. J. 1980 The evolution of slender inviscid drops in an axisymmetric straining flow. J. Fluid Mech. 101, 545–553.10.1017/S0022112080001784Google Scholar
Hinch, E. J. & Acrivos, A. 1979 Steady long slender droplets in two-dimensional straining motion. J. Fluid Mech. 91, 401–414.10.1017/S0022112079000227Google Scholar
Howell, P. D. & Siegel, M. 2004 The evolution of a slender non-axisymmetric drop in an extensional flow. J. Fluid Mech. 521, 155–180.10.1017/S002211200400148XGoogle Scholar
Levitskiy, S. P. & Shulman, Z. P. 1995 Bubbles in Polymeric Liquids. Technomic Publishing Company.Google Scholar
Milliken, W. J. & Leal, L. G. 1991 Deformation and breakup of viscoelastic drops in planar extensional flows. J. Non-Newtonian Fluid Mech. 40, 355–379.10.1016/0377-0257(91)87018-SGoogle Scholar
Rallison, J. M. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid. Mech. 16, 45–66.10.1146/annurev.fl.16.010184.000401Google Scholar
Sadhal, S. S., Ayyaswamy, P. S. & Chung, J. N. 1997 Transport Phenomena with Drops and Bubbles. Springer.10.1007/978-1-4612-4022-8Google Scholar
Sherwood, J. D. 1984 Tip streaming from slender drops in a nonlinear extensional flow. J. Fluid Mech. 144, 281–295.10.1017/S0022112084001609Google Scholar
Stone, H. A. 1994 Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid. Mech. 26, 65–102.10.1146/annurev.fl.26.010194.000433Google Scholar
Sumanasekara, U. R. & Bhattacharya, S. 2017 Detailed finer features in spectra of interfacial waves for characterization of a bubble-laden drop. J. Fluid Mech. 831, 698–718.10.1017/jfm.2017.607Google Scholar
Sumanasekara, U. R., Azese, M. N. & Bhattacharya, S. 2017 Transient penetration of a viscoelastic fluid in a narrow capillary channel. J. Fluid Mech. 830, 528–552.10.1017/jfm.2017.576Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A A146, 501–523.10.1098/rspa.1934.0169Google Scholar
Taylor, G. I. 1964 Conical free surfaces and fluid interfaces. In Proceedings of the 11th International Congress on Applied Mechanics, Munich, pp. 790–796. Springer.Google Scholar
Tretheway, D. C. & Leal, L. G. 1999 Surfactant and viscoelastic effects on drop deformation in 2-D extensional flow. AIChE J. 45, 929–937.10.1002/aic.690450503Google Scholar
Zapryanov, Z. & Tabakova, S. 1999 Dynamics of Bubbles, Drops and Rigid Particles. Kluwer Academic Publishers.10.1007/978-94-015-9255-0Google Scholar