A spherical vesicle is made up of a liquid core bounded by a semi-permeable membrane that is impermeable to solute molecules. When placed in an externally imposed gradient of solute concentration, the osmotic pressure jump across the membrane results in an inward trans-membrane solvent flux at the solute-depleted side of the vesicle, and and outward flux in its solute-enriched side. As a result, a freely suspended vesicle drifts down the concentration gradient, a phenomenon known as osmophoresis. An experimental study of lipid vesicles observed drift velocities that are more than three orders of magnitude larger than the linearised non-equilibrium prediction (Nardi et al., Phys. Rev. Lett., vol. 82, 1999, pp. 5168–5171). Inspired by this study, we analyse osmophoresis of a vesicle in close proximity to an impermeable wall, where the vesicle–wall separation $a\delta$ is small compared with the vesicle radius $a$. Due to intensification of the solute concentration gradient in the narrow gap between the membrane and the wall, the ‘osmophoretic’ force and torque on a stationary vesicle scale as an irrational power, $1/\sqrt {2}-1\ (\approx -0.29289\ldots )$, of $\delta$. Both the rectilinear velocity $\mathcal V$ and the angular velocity $\unicode {x1D6FA}$ of a freely suspended vesicle scale as the ratio of that power to $\ln \delta$. In contrast to the classical problem of sedimentation parallel to a wall, where the ratio $a\unicode {x1D6FA}/\mathcal V$ approaches $1/4$ as $\delta \to 0$, here the ratio approaches unity, as though the vesicle performs pure rigid-body rolling without slippage. Our approximations are in excellent agreement with hitherto unexplained numerical computations in the literature.

The system composed of a circular cylinder free to move along a transverse rectilinear path within a cross-current has often served as a canonical problem to study the vortex-induced vibrations (VIV) developing in the absence of structural restoring force, thus without structural natural frequency. The object of the present work is to extend the exploration of the behaviour of this system when the path is set to an arbitrary orientation, varying from the transverse to the streamwise direction, and the cylinder is forced to rotate about its axis. The investigation is conducted numerically at a Reynolds number equal to 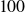$100$, based on the body diameter and oncoming flow velocity, for structure to displaced fluid mass ratios down to 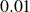$0.01$ and values of the rotation rate (ratio between body surface and oncoming flow velocities) ranging from 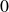$0$ to 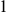$1$. When the transverse symmetry is broken by the orientation of the trajectory or the forced rotation, the cylinder drifts along the rectilinear path, at a velocity that can be predicted by a quasi-steady approach. Three distinct regimes are encountered: a pure drift regime, where the body translates at a constant velocity, and two oscillatory regimes, characterised by contrasted forms of displacement fluctuation about the drifting motion, but both closely connected to flow unsteadiness. VIV, nearly sinusoidal, persist over a wide range of path orientations, for all rotation rates. On the other hand, irregular jumps of the body, triggered by the rotation and named saccades, emerge when the trajectory is aligned, or almost aligned, with the current. The two forms of response differ by their regularity, but also by their amplitudes and frequencies, which deviate by one or more orders of magnitude. The rotation attenuates both VIV and saccades. Yet, an increase of the rotation rate enhances the erratic nature of the saccade regime.

In recent years, various unique properties of microswimmer suspensions have been revealed. Some microswimmers are deformable; however, the influence of the swimmer’s deformability has been overlooked. The present study examined the impact of soft microswimmers’ membrane deformations in a mono-dispersed dense suspension on microstructure formation. Due to the small size of the microswimmers, the flow field is described by the Stokes equation. The soft microswimmer was modelled as a capsule with a two-dimensional hyperelastic membrane enclosing a Newtonian fluid that is driven by propulsion torques distributed slightly above the membrane surface. Changes to the torque distribution caused the soft swimmer to exhibit different swimming modes as a pusher or puller. Similar to rigid squirmers, soft swimmers displayed self-organised local clusters in the suspension. Membrane deformation changed the mutual interference among swimmers in the cluster, bringing the interactions closer together than those of rigid squirmers. Especially among soft pushers, rotational diffusion due to hydrodynamic interference was reduced and the swimming trajectory became relatively straight. As a result, polar order was less likely to form, especially in regions of high $Ca$. On the other hand, pullers showed strong interactions due to retraction flow and an increase in mean membrane tension. For pushers (pullers), the rear (side) interaction produced the greatest change in tension. These findings are expected to be useful for effort to understand the propulsion mechanisms of medical and industrial soft microrobots, as well as the biological responses of microorganisms induced by mechanical stimuli.

Turbulent emulsions are ubiquitous in chemical engineering, food processing, pharmaceuticals and other fields. However, our experimental understanding of this area remains limited due to the multiscale nature of turbulent flow and the presence of extensive interfaces, which pose significant challenges to optical measurements. In this study, we address these challenges by precisely matching the refractive indices of the continuous and dispersed phases, enabling us to measure local velocity information at high volume fractions. The emulsion is generated in a turbulent Taylor–Couette flow, with velocity measured at two radial locations: near the inner cylinder (boundary layer) and in the middle gap (bulk region). Near the inner cylinder, the presence of droplets suppresses the emission of angular velocity plumes, which reduces the mean azimuthal velocity and its root mean squared fluctuation. The former effect leads to a higher angular velocity gradient in the boundary layer, resulting in greater global drag on the system. In the bulk region, although droplets suppress turbulence fluctuations, they enhance the cross-correlation between azimuthal and radial velocities, leaving the angular velocity flux contributed by the turbulent flow nearly unchanged. In both locations, droplets suppress turbulence at scales larger than the average droplet diameter and increase the intermittency of velocity increments. However, the effects of the droplets are more pronounced near the inner cylinder than in the bulk, likely because droplets fragment in the boundary layer but are less prone to break up in the bulk. Our study provides experimental insights into how dispersed droplets modulate global drag, coherent structures and the multiscale characteristics of turbulent flow.

The propagation of sound waves in high-temperature and plasma flows is subject to attenuation phenomena that alter both the wave amplitude and speed. This finite change in acoustic wave properties causes ambiguity in the definition of sound speed travelling through a chemically reactive medium. This paper proposes a novel computational study to address such a dependence of sound-wave propagation on non-equilibrium mechanisms. The methodology presented shows that the equations governing the space and time evolution of a small disturbance around an equilibrium state can be formulated as a generalised eigenvalue problem. The solution to this problem defines the wave structure of the flow and provides a rigorous definition of the speed of sound for a non-equilibrium flow along with its absorption coefficient. The method is applied to a two-temperature plasma evolving downstream of a shock, modelled using Park’s two-temperature model with 11 species for air. The numerical absorption coefficient at low temperatures shows excellent agreement with classical theory. At high temperatures, the model is validated for nitrogen and argon across wide temperature ranges with experimental values, showing that classical absorption theory is insufficient to characterise high-temperature flows due to the effect of finite-rate chemistry and vibrational relaxation. The speed of sound is verified in the frozen and equilibrium limits and its non-equilibrium profile is presented with and without viscous effects. It is furthermore shown that the variation in the speed of sound is driven by the dominating reaction mechanisms that the flow is subject to at different thermodynamic conditions.

Spontaneous flow reversals in buoyancy-driven flows are ubiquitous in many fields of science and engineering, often characterized by violent, intermittent occurrences. In this study, we present a complex-network-based reduced-order model to analyse intermittent events in turbulent flows, using temporal and spatial snapshot data. This framework combines elements of dynamical system theory with network science. We demonstrate its utility by applying it to data sequences from intermittent flow reversal events in two-dimensional thermal convection. This approach has proven robust in detecting and quantifying structures and predicting reversals. Additionally, it provides a perspective on the physical mechanisms underlying flow reversals through cluster evolution. This purely data-driven methodology shows the potential to enhance our understanding, prediction and control of turbulent flows and complex systems.

In rotating convection, analysis of heat transfer reveals a distinct shift in behaviour as the system transitions from a steep scaling regime near the onset of convection to a shallower scaling at higher Rayleigh numbers ($Ra$), irrespective of whether the top and bottom plates have stress-free, no-slip or no boundaries (homogeneous convection). However, while most research on this transition focuses on no-slip boundary conditions, geophysical and astrophysical flows commonly involve stress-free and homogeneous convection models as well. This study delves into the transition from the rapidly rotating regime to the non-rotating one with both stress-free and homogeneous models, leveraging direct numerical simulations (DNS) and existing literature data. Our findings unveil that for stress-free boundary conditions, the transitional Rayleigh number ($Ra_T$) exhibits a relationship $Ra_T\sim Ek^{-12/7}$, whereas for homogeneous rotating convection, $Ra_T\sim Ek^{-2}\, Pr$, where $Ek$ denotes the Ekman number, and $Pr$ denotes the Prandtl number. Both of these relationships align with the data obtained through DNS.

This study examines the effect of nozzle flexibility on vortex ring formation at a Reynolds Number of Re = 1000. The flexible nozzles impart elastic energy to the flow, increasing the hydrodynamic impulse of the vortex ring dependent on the input fluid acceleration and the initial nozzle tip deflection (predicted by the measured nozzle damped natural frequency). When these time scales are synchronised, the output velocity and hydrodynamic impulse of the vortex ring are maximised. Vortex ring pinch-off is predicted using the output velocity for each nozzle and is confirmed with closed finite time Lypunov exponent contours. The lowest tested input formation length, L/D = 1, where L is the piston stroke length and D is the nozzle diameter, generates a greater increase in impulse than L/D = 2 and L/D = 4, due to a higher relative increase in total ejected volume and by remaining in the single vortex formation regime. At L/D = 2 and L/D = 4, multiple vortex structures are observed due to the interplay of the counter-flow generated by the nozzles re-expanding and the steady input flow. At the end of the pumping cycle, during fluid deceleration, the flexible nozzles collapse. This helps in suppressing unfavourable negative pressure regions from forming within the nozzle, instead expelling additional fluid from the nozzle. Upon reopening, beneficial stopping vortices form within the nozzles, with circulation correlated to nozzle stiffness. This highlights a secondary optimal stiffness criterion that must be considered in a full-cycle analysis: the nozzle must be compliant enough to collapse during deceleration, yet remain as stiff as possible to reopen quickly to maximise efficiency in refilling.

In inviscid, incompressible flows, the evolution of vorticity is exactly equivalent to that of an infinitesimal material line-element and, hence, vorticity can be traced forward or backward in time in a Lagrangian fashion. This elegant and powerful description is not possible in viscous flows due to the action of diffusion. Instead, a stochastic Lagrangian interpretation is required and was recently introduced, where the origin of vorticity at a point is traced back in time as an expectation over the contribution from stochastic trajectories. We herein introduce for the first time an Eulerian, adjoint-based approach to quantify the back-in-time origin of vorticity in viscous, incompressible flows. The adjoint variable encodes the advection, tilting and stretching of the earlier-in-time vorticity that ultimately leads to the target value. Precisely, the adjoint vorticity is the volume-density of the mean Lagrangian deformation of the earlier vorticity. The formulation can also account for the injection of vorticity into the domain at solid boundaries. We demonstrate the mathematical equivalence of the adjoint approach and the stochastic Lagrangian approach. We then provide an example from turbulent channel flow, where we analyse the origin of high streamwise wall-shear-stress events and relate them to Lighthill’s mechanism of stretching of near-wall vorticity.

Combined theoretical and quantitative experimental study of resonant internal standing waves in a pycnocline between two miscible liquids in a narrow rectangular basin is presented. The waves are excited by a cylinder that harmonically oscillates in the vertical direction. A linear theoretical model describing the internal wave structure that accounts for pycnocline thickness, the finite wavemaker size and dissipation is developed. Separate series of measurements were performed using shadowgraphy and time-resolved particle image velocimetry. Accurate density profile measurements were carried out to monitor the variation of the pycnocline parameters in the course of the experiments; these measurements were used as the input parameters for the model simulations. The detected broadening of the pycnocline is attributed mainly to the presence of the waves and leads to the variation of the wave structure. The complex spatio-temporal structure of the observed internal wavefield was elucidated by carrying band-pass filtering in the temporal domain. The experiments demonstrate the coexistence of multiple spatial modes at the forcing frequency as well as the presence of the internal wave system at the second harmonic of the forcing frequency. The results of the theoretical model are in good agreement with the experiments.

This paper investigates the linear and nonlinear dynamics of two-dimensional penetrative convection subjected to radiative volumetric thermal forcing, focusing on ice-covered freshwater systems. Linear stability analysis reveals how critical wavenumbers $k_c$ and Rayleigh numbers $Ra_c$ are influenced by the attenuation lengths and incoming heat flux. In this configuration, the system easily becomes unstable with a small $Ra_c$, which is two decades smaller than that of the classical Rayleigh–Bénard convection problem, with typically $O(10)$. Weakly nonlinear analysis figures out that this configuration is supercritical, contrasting with the subcritical case by Veronis (Astrophys. J., vol. 137, 1963, 641–663). Numerical bifurcation solutions are performed from the critical points and over several decades, up to $Ra \sim O(10^6)$. This paper found that the system exhibits multiple steady solutions, and under certain specific conditions, a staircase temperature profile emerges. Meanwhile, we further discuss the influence of incoming heat flux and the Prandtl number $Pr$ on the primary bifurcation. Direct numerical simulations are also carried out, showing that heat is transported more efficiently via unsteady convection.

A linear stability analysis of a soluble surfactant-laden liquid film flowing down a compliant substrate is performed. Our purpose is to expand the prior studies (Carpenter and Garrad 1985 J. Fluid Mech. 155, 465–510; Alexander et al., 2020 J. Fluid Mech. 900, A40) by incorporating a soluble surfactant into the flow configuration. As a result, we formulate the Orr–Sommerfeld-type boundary value problem and solve it analytically by using the long-wave series expansion as well as numerically by using the Chebyshev spectral collocation method in an arbitrary wavenumber regime for infinitesimal disturbances. The long-wave result reveals that surface instability is stabilized in the presence of a surfactant, whereas it is destabilized in the presence of a compliant substrate. These opposing impacts suggest an analytical relationship between parameters associated with the soluble surfactant and compliant wall, ensuring the same critical Reynolds number for the emergence of surface instability corresponding to both surfactant-laden film flow over a compliant wall and surfactant-free film flow over a non-compliant wall. In the arbitrary wavenumber regime, along with the surface mode, we identify two additional modes based on their distinct phase speeds. Specifically, the wall mode emerges in the finite wavenumber regime, while the shear mode emerges only when the Reynolds number is large. As the surfactant Marangoni number increases, the wall mode destabilizes, resulting in a different outcome from the surface mode. Moreover, increasing the value of the ratio of adsorption and desorption rate constants stabilizes surface instability but destabilizes wall mode instability. As a result, we perceive that the soluble surfactant-laden film flow is linearly more unstable than the insoluble one due to surface instability but linearly more stable than the insoluble one due to wall mode instability. Additionally, we see a peculiar behaviour of base surface surfactant concentration on the primary instability. In fact, it has a specific value depending on adsorption and desorption rate constants below which surface instability stabilizes but wall mode instability destabilizes, whereas above which an opposite phenomenon occurs. Finally, in the high-Reynolds-number regime, we can suppress shear mode instability by raising the surfactant Marangoni number and the ratio of adsorption and desorption rate constants when the angle of inclination is sufficiently small. Unlike surface instability, the base surface surfactant concentration exhibits both stabilizing and destabilizing influences on shear mode instability.

While we now have a relatively good understanding of low-Reynolds-number hydrodynamics, and elegant techniques to dissect it, one cannot truly say the same for yield-stress fluids. For these materials, the nonlinearity associated with the yield stress complicates analysis and prevents the use of many of the techniques used for slow viscous flow. Simultaneously, the presence of a yield stress introduces a range of new features into the problem beyond those of traditional Stokes flow. Accordingly, in this essay, we discuss the impact of a yield stress in the relatively simple setting of two-dimensional, steady, inertialess flow. The main goals are to establish intuition for the dramatically different features that can be introduced to the flow by the yield stress, and to outline the various tools available to the modeller to construct and interpret these flows.

Developing a consistent near-wall turbulence model remains an unsolved problem. The machine learning method has the potential to become the workhorse for turbulence modelling. However, the learned model suffers from limited generalisability, especially for flows without similarity laws (e.g. separated flows). In this work, we propose a knowledge-integrated additive (KIA) learning approach for learning wall models in large-eddy simulations. The proposed approach integrates the knowledge in the simplified thin-boundary-layer equation with a data-driven forcing term for the non-equilibrium effects induced by pressure gradients and flow separations. The capability learned from each flow dataset is encapsulated using basis functions with the corresponding weights approximated using neural networks. The fusion of capabilities learned from various datasets is enabled using a distance function, in a way that the learned capability is preserved and the generalisability to other cases is allowed. The additive learning capability is demonstrated via training the model sequentially using the data of the flow with pressure gradient but no separation, and the separated flow data. The capability of the learned model to preserve previously learned capabilities is tested using turbulent channel flow cases. The periodic hill and the 2-D Gaussian bump cases showcase the generalisability of the model to flows with different surface curvatures and different Reynolds numbers. Good agreements with the references are obtained for all the test cases.

A reactive control strategy is implemented to attenuate the streaks formed on a wing boundary layer due to free-stream turbulence (FST). Numerical simulations are performed on a section of a NACA0008 profile, considering its leading edge, while forced by FST with turbulence intensities of 0.5 % and 2.5 %. The controller is composed of localised sensors and actuators, with the control law consisting of a linear quadratic Gaussian regulator designed on a reduced-order model based only on the impulse responses of the system. Three configurations are evaluated by considering three different numbers of sensors/actuators along the spanwise direction. It is found that all configurations are effective in damping the streaks inside the boundary layer, whose effect is sustained downstream of the objective function location. However, distinct behaviours are observed when comparing the capability of the controllers with delay transition, where the best performance is attained for the case with larger number of sensors/actuators. This is attributed to the effectiveness of the controller in damping the streaks that will later break down, which in this case are associated with relatively short spanwise wavelength. This observation is confirmed by analysing the stability of the flow before the appearance of turbulent spots. Our results suggest that for an effective transition delay, efforts should not only be put into control of streaks with average spanwise wavelength, but also in the short spanwise wavelength associated with breakdown.

In this study, we investigate the sedimentation of spheroidal particles in an initially quiescent fluid by means of particle-resolved direct numerical simulations. Settling particles with three different shapes – oblate spheroid, sphere and prolate spheroid – but fixed Galileo number $Ga=80$ and density ratio $\gamma =2$ at volume fraction $\phi =1\%$ are considered. Oblate and prolate particles are found to form column-like clusters as a consequence of the wake-induced hydrodynamic interactions in the suspension. This effect, together with the change of particle orientation, enhances the mean settling velocity of the dispersed phase. In contrast, spherical particles do not exhibit clustering, and settle with hindered velocity in the suspension. Furthermore, we focus on the pseudo-turbulence induced by the settling particles. We report a non-Gaussian distribution of the fluid velocity and a robust $-3$ power law of the energy spectra. By scrutinizing the scale-by-scale budget, we find that the anisotropy of the particle-induced pseudo-turbulence is manifested not only by the uneven allocation of turbulence kinetic energy among the different velocity components, but also by the anisotropic distribution of energy in spectral space. The fluid–particle interactions inject energy into the vertical velocity component, thus sustaining the turbulence, while pressure redistributes the kinetic energy among the different velocity components. The clustering of oblate/prolate particles significantly increases the energy input at large scales, forcing elongated flow structures. Moreover, the redistribution and nonlinear transfer of the energy are also intensified in the presence of particle clustering, which reduces the anisotropy of the particle-induced pseudo-turbulence.