Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-09T23:49:31.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Slender body theory for particles with non-circular cross-sections with application to particle dynamics in shear flows

Published online by Cambridge University Press:  02 September 2019

Neeraj S. Borker Open the ORCID record for Neeraj S. Borker [Opens in a new window]  and
Donald L. Koch Open the ORCID record for Donald L. Koch [Opens in a new window]
Neeraj S. Borker
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Donald L. Koch*
Affiliation:
Robert Frederick Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents a theory to obtain the force per unit length acting on a slender filament with a non-circular cross-section moving in a fluid at low Reynolds number. Using a regular perturbation of the inner solution, we show that the force per unit length has 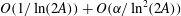$O(1/\ln (2A))+O(\unicode[STIX]{x1D6FC}/\ln ^{2}(2A))$ contributions driven by the relative motion of the particle and the local fluid velocity and an 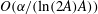$O(\unicode[STIX]{x1D6FC}/(\ln (2A)A))$ contribution driven by the gradient in the imposed fluid velocity. Here, the aspect ratio (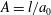$A=l/a_{0}$) is defined as the ratio of the particle size (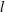$l$) to the cross-sectional dimension (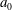$a_{0}$) and $\unicode[STIX]{x1D6FC}$ is the amplitude of the non-circular perturbation. Using thought experiments, we show that two-lobed and three-lobed cross-sections affect the response to relative motion and velocity gradients, respectively. A two-dimensional Stokes flow calculation is used to extend the perturbation analysis to cross-sections that deviate significantly from a circle (i.e. 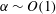$\unicode[STIX]{x1D6FC}\sim O(1)$). We demonstrate the ability of our method to accurately compute the resistance to translation and rotation of a slender triaxial ellipsoid. Furthermore, we illustrate novel dynamics of straight rods in a simple shear flow that translate and rotate quasi-periodically if they have two-lobed cross-section, and rotate chaotically and translate diffusively if they have a combination of two- and three-lobed cross-sections. Finally, we show the remarkable ability of our theory to accurately predict the motion of rings, retaining great accuracy for moderate aspect ratios (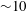${\sim}10$) and cross-sections that deviate significantly from a circle, thereby making our theory a computationally inexpensive alternative to other Stokes flow solvers.

JFM classification

Low-Reynolds-number flows: Slender-body theory Mathematical Foundations: Computational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 1098 - 1133
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Shaqfeh, E. S. G. 1988 The effective thermal conductivity and elongational viscosity of a nondilute suspension of aligned slender rods. Phys. Fluids 31, 1841–1844.10.1063/1.866681Google Scholar
Anczurowski, E. & Mason, S. G. 1968 Particle motions in sheared suspension. XXIV. Rotations of rigid spheroids and cylinders. Trans. Soc. Rheol. 12, 209–215.10.1122/1.549106Google Scholar
Batchelor, G. K. 1954 The skin friction on infinite cylinders moving parallel to their length. Q. J. Mech. Appl. Maths 7 (2), 179–192.10.1093/qjmam/7.2.179Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44 (3), 419–440.10.1017/S002211207000191XGoogle Scholar
Beckers, K. F., Koch, D. L. & Tester, J. W. 2015 Slender-body theory for transient heat conduction: theoretical basis, numerical implementation and case studies. Proc. R. Soc. Lond. A 471 (2184), 20150494.Google Scholar
Berg, H. C. & Anderson, R. A. 1973 Bacteria swim by rotating their flagellar filaments. Nature 245, 380–382.10.1038/245380a0Google Scholar
Borker, N. S., Stroock, A. D. & Koch, D. L. 2018 Controlling rotation and migration of rings in a simple shear flow through geometric modifications. J. Fluid Mech. 840, 379–407.10.1017/jfm.2018.20Google Scholar
Bray, D. 2000 Cell Movements. Garland.Google Scholar
Brennen, C. & Winet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9, 339–398.10.1146/annurev.fl.09.010177.002011Google Scholar
Brenner, H. 1964 The Stokes resistance of an arbitrary particle. 3. Shear fields. Chem. Engng Sci. 19, 631–651.10.1016/0009-2509(64)85052-1Google Scholar
Bretherton, F. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14 (2), 284–304.10.1017/S002211206200124XGoogle Scholar
Chen, H. S. & Acrivos, A. 1976 On the effective thermal conductivity of dilute suspensions containing highly conducting slender inclusions. Proc. R. Soc. Lond. A 349, 261–276.10.1098/rspa.1976.0072Google Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 44 (4), 791–810.10.1017/S002211207000215XGoogle Scholar
Cox, R. G. 1971 The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 45 (4), 625–657.10.1017/S0022112071000259Google Scholar
Einarsson, J., Mihiretie, B. M., Laas, A., Ankardal, S., Angilella, J. R., Hanstorp, D. & Mehlig, B. 2016 Tumbling of asymmetric microrods in a microchannel flow. Phys. Fluid 28, 013302.10.1063/1.4938239Google Scholar
Foulds, I. G. & Parameswaran, M. 2006 A planar self-sacrificial multilayer SU-8-based MEMS process utilizing a UV-blocking layer for the creation of freely moving parts. J. Micromech. Microengng 16 (10), 2109–2115.10.1088/0960-1317/16/10/026Google Scholar
Fredrickson, G. H. & Shaqfeh, E. S. G. 1989 Heat and mass transport in composites of aligned slender fibers. Phys. Fluids A 1, 3–20.10.1063/1.857546Google Scholar
Gao, W. & Wang, J. 2014 The environmental impact of micro/nanomachines: a review. ACS Nano 8 (4), 3170–3180.10.1021/nn500077aGoogle Scholar
Guasto, J. S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.10.1146/annurev-fluid-120710-101156Google Scholar
Isla, A., Brostow, W., Bujard, B., Esteves, M., Rodriguez, J. R., Vargas, S. & Castano, V. M. 2003 Nanohybrid scratch resistant coatings for teeth and bone viscoelasticity manifested in tribology. Mat. Res. Innovat. 7, 110–114.10.1080/14328917.2003.11784770Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.10.1098/rspa.1922.0078Google Scholar
Johnson, R. E. 1980 An improved slender-body theory for Stokes flow. J. Fluid Mech. 99 (2), 411–431.10.1017/S0022112080000687Google Scholar
Johnson, R. E. & Brokaw, C. J. 1979 Flagellar hydrodynamics. A comparison between resistive-force theory and slender-body theory. Biophys. J. 25, 113–127.10.1016/S0006-3495(79)85281-9Google Scholar
Jones, R. T.1946 Properties of low-aspect-ratio pointed wings at speeds below and above the speed of sound. NACA Tech. Rep. 835.Google Scholar
Keller, J. & Rubinow, S. 1976 Slender-body theory for slow viscous flow. J. Fluid Mech. 75 (4), 705–714.10.1017/S0022112076000475Google Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.10.1017/S0022112089003174Google Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics. Dover.Google Scholar
Kim, Y. J. & Rae, W. J. 1991 Separation of screw-sensed particles in a homogeneous shear field. Intl J. Multiphase Flow 17 (6), 717–744.10.1016/0301-9322(91)90053-6Google Scholar
Koens, L. & Lauga, E. 2016 Slender-ribbon theory. Phys. Fluids 28 (1), 013101.10.1063/1.4938566Google Scholar
Lamb, S. H. 1932 Hydrodynamics. The University Press.Google Scholar
Lighthill, M. J. 1960 Note on the swimming of slender fish. J. Fluid Mech. 9, 305–317.10.1017/S0022112060001110Google Scholar
Lighthill, M. J. 1971 Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179, 125–138.Google Scholar
Lopez, M. & Graham, M. D. 2007 Shear-induced diffusion in dilute suspensions of spherical or non-spherical particles: effects of irreversibility and symmetry breaking. Phys. Fluids 19, 073602.10.1063/1.2750525Google Scholar
Mackaplow, M. B & Shaqfeh, E. S. G. 1996 A numerical study of the rheological properties of suspensions of rigid, non-Brownian fibres. J. Fluid Mech. 329, 155–186.10.1017/S0022112096008889Google Scholar
Mackaplow, M. B & Shaqfeh, E. S. G. 1998 A numerical study of the sedimentation of fibre suspensions. J. Fluid Mech. 376, 149–182.10.1017/S0022112098002663Google Scholar
Mackaplow, M. B, Shaqfeh, E. S. G. & Schiek, R. L. 1994 A numerical study of heat and mass transport in fibre suspensions. Proc. R. Soc. Lond. A 447, 77–110.10.1098/rspa.1994.0130Google Scholar
Munk, M. M.1924 The aerodynamic forces on airship hulls. NACA Tech. Rep. 184.Google Scholar
Newman, J. N. 1964 A slender-body theory for ship oscillations in waves. J. Fluid Mech. 18, 602–618.10.1017/S0022112064000441Google Scholar
Newman, J. N. 1970 Applications of slender-body theory in ship hydrodynamics. Annu. Rev. Fluid Mech. 2, 67–94.10.1146/annurev.fl.02.010170.000435Google Scholar
Paulsen, K. S., Di Carlo, D. & Chung, A. J. 2015 Optofluidic fabrication for 3D-shaped particles. Nat. Commun. 6, 6976.10.1038/ncomms7976Google Scholar
Pozrikidis, C. 2002 A Practical Guide to Boundary Element Methods With the Software Library BEMLIB. Chapman and Hall/CRC.10.1201/9781420035254Google Scholar
Rahnama, M., Koch, D. L., Iso, Y. & Cohen, C. 1993 Hydrodynamic, translational diffusion in fiber suspensions subject to simple shear flow. Phys. Fluids A 5 (4), 849–862.10.1063/1.858890Google Scholar
Rahnama, M., Koch, D. L. & Shaqfeh, E. S. G. 1995 The effect of hydrodynamic interactions on the orientation distribution in a fiber suspension subject to simple shear flow. Phys. Fluids 7 (3), 487–506.10.1063/1.868647Google Scholar
Raney, J. R. & Lewis, J. A. 2015 Printing mesoscale architectures. MRS Bull. 40 (11), 943–950.10.1557/mrs.2015.235Google Scholar
Rocha, A. & Acrivos, A. 1973a On the effective thermal conductivity of dilute dispersions: general theory for inclusions of arbitrary shape. Q. J. Mech. Appl. Maths 26, 217–233.10.1093/qjmam/26.2.217Google Scholar
Rocha, A. & Acrivos, A. 1973b On the effective thermal conductivity of dilute dispersions: highly conducting inclusions of arbitrary shape. Q. J. Mech. Appl. Maths 26, 441–455.10.1093/qjmam/26.4.441Google Scholar
Sacanna, S., Korpics, M., Rodriguez, K., Colón-Meléndez, L., Kim, S.-H., Pine, D. J. & Yi, G.-R. 2013 Shaping colloids for self-assembly. Nat. Commun. 4, 1688.10.1038/ncomms2694Google Scholar
Shaqfeh, E. S. G. 1988 A nonlocal theory for the heat transport in composites containing highly conducting fibrous inclusions. Phys. Fluids 31, 2405–2425.10.1063/1.866594Google Scholar
Singh, V., Koch, D. L. & Stroock, A. D. 2013 Rigid ring-shaped particles that align in simple shear flow. J. Fluid Mech. 722, 121–158.10.1017/jfm.2013.53Google Scholar
Singh, V., Koch, D. L., Subramanian, G. & Stroock, A. D. 2014 Rotational motion of a thin axisymmetric disk in a low Reynolds number linear flow. Phys. Fluids 26 (3), 033303.10.1063/1.4868520Google Scholar
Soler, L. & Sánchez, S. 2014 Catalytic nanomotors for environmental monitoring and water remediation. Nanoscale 6 (13), 7175–7182.10.1039/C4NR01321BGoogle Scholar
Suarez, S. S. & Pacey, A. A. 2006 Sperm transport in the female reproductive tract. Hum. Reprod. Update 12 (1), 23–37.10.1093/humupd/dmi047Google Scholar
Tekce, H. S., Kumlutas, D. & Tavman, I. H. 2007 Effect of particle shape on thermal conductivity of copper reinforced polymer composites. J. Reinf. Plast. Comp. 26 (1), 113–121.10.1177/0731684407072522Google Scholar
Wang, J., Graham, M. D. & Klingenberg, D. J. 2014 Shear-induced diffusion in dilute curved fiber suspensions in simple shear flow. Phys. Fluids 26 (3), 033301.10.1063/1.4867171Google Scholar
Wang, J., Tozzi, E. J., Graham, M. D. & Klingenberg, D. J. 2012 Flipping, scooping, and spinning: drift of rigid curved nonchiral fibers in simple shear flow. Phys. Fluids 24, 123304.10.1063/1.4769980Google Scholar
Yarin, A. L., Gottlieb, O. & Roisman, I. V. 1997 Chaotic rotation of triaxial ellipsoids in simple shear flow. J. Fluid Mech. 340, 83–100.10.1017/S0022112097005260Google Scholar
Youngren, G. K. & Acrivos, A. 1975 Stokes flow past a particle of arbitrary shape: a numerical method of solution. J. Fluid Mech. 69 (02), 377–403.10.1017/S0022112075001486Google Scholar
Supplementary material: File

Borker and Koch supplementary material

Borker and Koch supplementary material

Download Borker and Koch supplementary material(File)
File 347.8 KB