Let $\mathcal{S}$ denote the set of integers representable as a sum of two squares. Since $\mathcal{S}$ can be described as the unsifted elements of a sieving process of positive dimension, it is to be expected that $\mathcal{S}$ has many properties in common with the set of prime numbers. In this paper we exhibit “unexpected irregularities” in the distribution of sums of two squares in short intervals, a phenomenon analogous to that discovered by Maier, over a decade ago, in the distribution of prime numbers. To be precise, we show that there are infinitely many short intervals containing considerably more elements of $\mathcal{S}$ than expected, and infinitely many intervals containing considerably fewer than expected.

We develop a scattering theory for perturbations of powers of the Laplacian on asymptotically Euclidean manifolds. The (absolute) scattering matrix is shown to be a Fourier integral operator associated to the geodesic flow at time $\pi $ on the boundary. Furthermore, it is shown that on ${{\mathbb{R}}^{n}}$ the asymptotics of certain short-range perturbations of ${{\Delta }^{k}}$ can be recovered from the scattering matrix at a finite number of energies.

We will construct a finite union of finite quotients of the affine building of the group $\text{G}{{\text{L}}_{3}}$ over the field of $p$-adic numbers ${{\mathbb{Q}}_{p}}$. We will view this object as a hypergraph and estimate the spectrum of its underlying graph.

For a reductive $p$-adic group $G$, we compute the supports of the Hecke algebras for the $K$-types for $G$ lying in a certain frequently-occurring class. When $G$ is classical, we compute the intertwining between any two such $K$-types.

Using Local Residues and the Duality Principle a multidimensional variation of the completeness theorems by T. Carleman and A. F. Leontiev is proven for the space of holomorphic functions defined on a suitable open strip ${{T}_{\alpha }}\,\subset \,{{\mathbf{C}}^{2}}$. The completeness theorem is a direct consequence of the Cauchy Residue Theorem in a torus. With suitable modifications the same result holds in ${{\mathbf{C}}^{n}}$.

In this paper we show that for a Grothendieck category $\mathcal{A}$ and a complex $E$ in $\mathbf{C}(\mathcal{A})$ there is an associated localization endofunctor $\ell$ in $\mathbf{D}(\mathcal{A})$. This means that $\ell$ is idempotent (in a natural way) and that the objects that go to 0 by $\ell$ are those of the smallest localizing (= triangulated and stable for coproducts) subcategory of $\mathbf{D}(\mathcal{A})$ that contains $E$. As applications, we construct $\text{K}$-injective resolutions for complexes of objects of $\mathcal{A}$ and derive Brown representability for $\mathbf{D}(\mathcal{A})$ from the known result for $\mathbf{D}(R-\mathbf{mod})$, where $R$ is a ring with unit.

The nonlinear Sturm-Liouville equation

$$-{{\left( p{y}' \right)}^{\prime }}\,+\,qy\,=\,\text{ }\!\!\lambda\!\!\text{ }\left( 1-f \right)ry\,on\,[0,\,1]$$

is considered subject to the boundary conditions

$$\left( {{\text{a}}_{j}}\text{ }\lambda \text{ }\text{+}{{\text{b}}_{j}} \right)y\left( j \right)=\left( {{c}_{j}}\text{ }\lambda \text{ }+{{d}_{j}} \right)\left( p{y}' \right)\left( j \right),j=0,1$$

Here ${{\text{a}}_{0}}\,=\,0\,=\,{{c}_{0}}$ and $p,\,r\,>\,0$ and $q$ are functions depending on the independent variable $x$ alone, while $f$ depends on $x,\,y\,and\,{y}'$. Results are given on existence and location of sets of $(\lambda ,\,y)$ bifurcating from the linearized eigenvalues, and for which $y$ has prescribed oscillation count, and on completeness of the $y$ in an appropriate sense.

We present “reiteration theorems” with limiting values $\theta =0$ and $\theta =1$ for a real interpolation method involving broken-logarithmic functors. The resulting spaces lie outside of the original scale of spaces and to describe them new interpolation functors are introduced. For an ordered couple of (quasi-) Banach spaces similar results were presented without proofs by Doktorskii in $[\text{D}]$.

Two-weight inequalities of strong and weak type are obtained in the context of spaces of homogeneous type. Various applications are given, in particular to Cauchy singular integrals on regular curves.

In this paper, we revisit Russell-type modular equations, a collection of modular equations first studied systematically by R. Russell in 1887. We give a proof of Russell’s main theorem and indicate the relations between such equations and the constructions of Hilbert class fields of imaginary quadratic fields. Motivated by Russell’s theorem, we state and prove its cubic analogue which allows us to construct Russell-type modular equations in the theory of signature 3.

We describe the embedded resolution of an irreducible quasi-ordinary surface singularity $\left( V,\,p \right)$ which results from applying the canonical resolution of Bierstone-Milman to $\left( V,\,p \right)$. We show that this process depends solely on the characteristic pairs of $\left( V,\,p \right)$, as predicted by Lipman. We describe the process explicitly enough that a resolution graph for $f$ could in principle be obtained by computer using only the characteristic pairs.

Given a holomorphic Hilbertian bundle on a compact complex manifold, we introduce the notion of holomorphic ${{L}^{2}}$ torsion, which lies in the determinant line of the twisted ${{L}^{2}}$ Dolbeault cohomology and represents a volume element there. Here we utilise the theory of determinant lines of Hilbertian modules over finite von Neumann algebras as developed in $[\text{CFM}]$. This specialises to the Ray-Singer-Quillen holomorphic torsion in the finite dimensional case. We compute a metric variation formula for the holomorphic ${{L}^{2}}$ torsion, which shows that it is not in general independent of the choice of Hermitian metrics on the complex manifold and on the holomorphic Hilbertian bundle, which are needed to define it. We therefore initiate the theory of correspondences of determinant lines, that enables us to define a relative holomorphic ${{L}^{2}}$ torsion for a pair of flat Hilbertian bundles, which we prove is independent of the choice of Hermitian metrics on the complex manifold and on the flat Hilbertian bundles.

Explicit evaluations of the symmetric Euler integral $\int _{0}^{1}\,{{u}^{\alpha }}{{(1-u)}^{\alpha }}f(u)\,du$ are obtained for some particular functions $f$. These evaluations are related to duplication formulae for Appell’s hypergeometric function ${{F}_{1}}$ which give reductions of ${{F}_{1}}(\alpha ,\beta ,\beta ,2\alpha ,y,z)$ in terms of more elementary functions for arbitrary $\beta $ with $z=y/(y-1)$ and for $\beta =\alpha +\frac{1}{2}$ with arbitrary $y,z$. These duplication formulae generalize the evaluations of some symmetric Euler integrals implied by the following result: if a standard Brownian bridge is sampled at time 0, time 1, and at $n$ independent randomtimes with uniformdistribution on $[0,1]$, then the broken line approximation to the bridge obtained from these $n+2$ values has a total variation whose mean square is $n(n+1)/(2n+1)$.

The ‘1-loop partition function’ of a rational conformal field theory is a sesquilinear combination of characters, invariant under a natural action of $\text{S}{{\text{L}}_{2}}(\mathbb{Z})$, and obeying an integrality condition. Classifying these is a clearly defined mathematical problem, and at least for the affine Kac-Moody algebras tends to have interesting solutions. This paper finds for each affine algebra $B_{r}^{\left( 1 \right)}$ and $D_{r}^{(1)}$ all of these at level $k\le 3$. Previously, only those at level 1 were classified. An extraordinary number of exceptionals appear at level 2—the $B_{r}^{(1)},D_{r}^{(1)}$ level 2 classification is easily the most anomalous one known and this uniqueness is the primary motivation for this paper. The only level 3 exceptionals occur for $B_{2}^{(1)}\cong C_{2}^{(1)}$ and $D_{7}^{(1)}$. The ${{B}_{2,3}}$ and ${{D}_{7,3}}$ exceptionals are cousins of the ${{\varepsilon }_{6}}$-exceptional and ${{\varepsilon }_{8}}$-exceptional, respectively, in the $\text{A-D-E}$ classification for $A_{1}^{(1)}$, while the level 2 exceptionals are related to the lattice invariants of affine $u(1)$.

We construct an automorphic realization of the global minimal representation of quaternionic exceptional groups, using the theory of Eisenstein series, and use this for the study of theta correspondences.

We prove that two, apparently different, class-group valued Galois module structure invariants associated to the algebraic $K$-groups of rings of algebraic integers coincide. This comparison result is particularly important in making explicit calculations.

We study 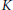$K$-orbits in 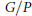$G/P$ where 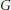$G$ is a complex connected reductive group, $P\,\subseteq \,G$ is a parabolic subgroup, and 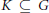$K\,\subseteq \,G$ is the fixed point subgroup of an involutive automorphism 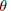$\theta$. Generalizing work of Springer, we parametrize the (finite) orbit set 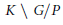$K\,\backslash \,G/P$ and we determine the isotropy groups. As a consequence, we describe the closed (resp. affine) orbits in terms of 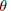$\theta$-stable (resp. 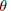$\theta$-split) parabolic subgroups. We also describe the decomposition of any 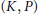$(K,\,P)$-double coset in 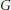$G$ into 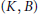$(K,\,B)$-double cosets, where 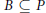$B\,\subseteq \,P$ is a Borel subgroup. Finally, for certain 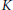$K$-orbit closures 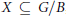$X\,\subseteq \,G/B$, and for any homogeneous line bundle 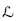$\mathcal{L}$ on 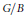$G/B$ having nonzero global sections, we show that the restriction map 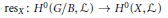$\text{re}{{\text{s}}_{X}}\,:\,{{H}^{0}}\,\left( G\,/\,B,\,\mathcal{L} \right)\,\to \,{{H}^{0}}\,\left( X,\,\mathcal{L} \right)$ is surjective and that 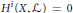${{H}^{i}}\,\left( X,\mathcal{L} \right)\,=\,0$ for 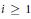$i\,\ge \,1$. Moreover, we describe the 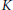$K$-module 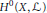${{H}^{0}}\left( X,L \right)$. This gives information on the restriction to 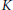$K$ of the simple 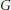$G$-module 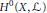${{H}^{0}}\,\left( G\,/\,B,\mathcal{L} \right)$. Our construction is a geometric analogue of Vogan and Sepanski’s approach to extremal 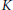$K$-types.

A simple ${{C}^{*}}$-algebra is constructed for which the Murray-von Neumann equivalence classes of projections, with the usual addition—induced by addition of orthogonal projections—form the additive semigroup

$$\left\{ 0,\,2,\,3,\ldots \right\}.$$

(This is a particularly simple instance of the phenomenon of perforation of the ordered ${{K}_{0}}$-group, which has long been known in the commutative case—for instance, in the case of the four-sphere—and was recently observed by the second author in the case of a simple ${{C}^{*}}$-algebra.)

Let $G$ be a connected reductive $p$-adic group and let $\mathfrak{g}$ be its Lie algebra. Let $\mathcal{O}$ be any $G$-orbit in $\mathfrak{g}$. Then the orbital integral ${{\mu }_{\mathcal{O}}}$ corresponding to $\mathcal{O}$ is an invariant distribution on $\mathfrak{g}$, and Harish-Chandra proved that its Fourier transform ${{\hat{\mu }}_{\mathcal{O}}}$ is a locally constant function on the set ${\mathfrak{g}}'$ of regular semisimple elements of $\mathfrak{g}$. If $\mathfrak{h}$ is a Cartan subalgebra of $\mathfrak{g}$, and $\omega $ is a compact subset of $\mathfrak{h}\,\cap \,{\mathfrak{g}}'$, we give a formula for ${{\hat{\mu }}_{\mathcal{O}}}\left( tH \right)$ for $H\,\in \,\omega $ and $t\,\in \,{{F}^{\times }}$ sufficiently large. In the case that $\mathcal{O}$ is a regular semisimple orbit, the formula is already known by work of Waldspurger. In the case that $\mathcal{O}$ is a nilpotent orbit, the behavior of ${{\hat{\mu }}_{\mathcal{O}}}$ at infinity is already known because of its homogeneity properties. The general case combines aspects of these two extreme cases. The formula for ${{\hat{\mu }}_{\mathcal{O}}}$ at infinity can be used to formulate a “theory of the constant term” for the space of distributions spanned by the Fourier transforms of orbital integrals. It can also be used to show that the Fourier transforms of orbital integrals are “linearly independent at infinity.”

We consider the problem

$$\left\{ \begin{matrix} {{\varepsilon }^{2}}\Delta u-u+f(u)=0,u>0 & \text{in}\,\Omega \\ \frac{\partial u}{\partial v}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & \text{on}\,\partial \Omega , \\\end{matrix} \right.$$

where $\Omega $ is a bounded smooth domain in ${{R}^{N}},\varepsilon >0$ is a small parameter and $f$ is a superlinear, subcritical nonlinearity. It is known that this equation possesses multiple boundary spike solutions that concentrate, as $\varepsilon $ approaches zero, at multiple critical points of the mean curvature function $H(P),P\in \partial \Omega $. It is also proved that this equation has multiple interior spike solutions which concentrate, as $\varepsilon \to 0$, at sphere packing points in $\Omega $.

In this paper, we prove the existence of solutions with multiple spikes both on the boundary and in the interior. The main difficulty lies in the fact that the boundary spikes and the interior spikes usually have different scales of error estimation. We have to choose a special set of boundary spikes to match the scale of the interior spikes in a variational approach.