Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T10:20:38.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Correspondences, von Neumann Algebras and Holomorphic L2 Torsion

Published online by Cambridge University Press:  20 November 2018

A. Carey ,
M. Farber  and
V. Mathai
A. Carey
Affiliation:
Department of Pure Mathematics, University of Adelaide, Adelaide 500, Australia email: [email protected]
M. Farber
Affiliation:
School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel email: [email protected]
V. Mathai
Affiliation:
Department of Pure Mathematics, University of Adelaide, Adelaide 5005, Australia email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a holomorphic Hilbertian bundle on a compact complex manifold, we introduce the notion of holomorphic 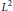${{L}^{2}}$ torsion, which lies in the determinant line of the twisted 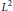${{L}^{2}}$ Dolbeault cohomology and represents a volume element there. Here we utilise the theory of determinant lines of Hilbertian modules over finite von Neumann algebras as developed in 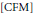$[\text{CFM}]$. This specialises to the Ray-Singer-Quillen holomorphic torsion in the finite dimensional case. We compute a metric variation formula for the holomorphic 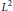${{L}^{2}}$ torsion, which shows that it is not in general independent of the choice of Hermitian metrics on the complex manifold and on the holomorphic Hilbertian bundle, which are needed to define it. We therefore initiate the theory of correspondences of determinant lines, that enables us to define a relative holomorphic 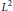${{L}^{2}}$ torsion for a pair of flat Hilbertian bundles, which we prove is independent of the choice of Hermitian metrics on the complex manifold and on the flat Hilbertian bundles.

Keywords

58J5258J3558J20Holomorphic L2 torsioncorrespondenceslocal index theoremalmost Kähler manifoldsvon Neumann algebrasdeterminant lines.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 4 , 01 August 2000 , pp. 695 - 736
Copyright
Copyright © Canadian Mathematical Society 2000

References

[ASS] Araki, H., Smith, M-S. B. and Smith, L., On the homotopical significance of the type of von Neumann algebra factors. Comm. Math. Phys. 22(1971), 71–88.Google Scholar
[BGV] Berline, N., Getzler, E. and Vergne, M., Heat kernels and Dirac operators. Springer Verlag, Grundlehren derMath.Wiss 298, 1992.Google Scholar
[Bi] Bismut, J. M., The local index theorem for non-Kähler manifolds. Math. Ann. 284(1989), 681–699.Google Scholar
[BF] Bismut, J. M. and Freed, D. S., The analysis of elliptic families, I. Metrics and connections on determinant lines. Comm. Math. Phys. 106(1986), 159–176.Google Scholar
[BGS] Bismut, J. M., Gillet, H. and Soule, C., Analytic torsion and holomorphic determinant bundles, I, II, III. Comm. Math. Phys. 115(1988), 49–78. 79–126, 301–351.Google Scholar
[B] Breuer, M., Fredholm Theories in von Neumann algebras I, II. Math. Ann. 178, 180(1968), (1969), 243–254, 313–325.Google Scholar
[BW] Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups and representations of reductive groups. Ann. of Math. Studies, Princeton University Press 94, 1980.Google Scholar
[BFKM] Burghelea, D., Friedlander, L., Kappeler, T. and McDonald, P., Analytic and Reidemeister torsion for representations in finite type Hilbert modules. Geophys. Astrophys. Fluid Dynamics 6(1996), 751–859.Google Scholar
[Cl] Clair, B., Residual amenability and the approximation of L2-invariants. Michigan Math. J. 46(1999), 331–346.Google Scholar
[CFM] Carey, A. L., Farber, M. and Mathai, V., Determinant Lines, von Neumann algebras and L2 torsion. Crelle J. 484(1997), 153–181.Google Scholar
[CH] Comtet, A. and Houston, P. J., Effective action on the hyperbolic plane in a constant external field. J. Math. Phys. 26(1985), 185–191.Google Scholar
[Dix] Dixmier, J., Von Neumann algebras. North Holland, Amsterdam, 1981.Google Scholar
[DD] Dixmier, J. and Douady, A., Champs continus d’espaces hilbertiens et de C*-algebres. Bull. Soc. Math. France 91(1963), 227–284.Google Scholar
[DM] Dodziuk, J. and Mathai, V., Approximating L2 invariants of amenable covering spaces: A Combinatorial Approach. J. Funct. Anal. 154(1998), 359–378.Google Scholar
[D] Donnelly, H., Local index theorem for families. Michigan Math. J. 35(1988), 11–20.Google Scholar
[F] Farber, M., Combinatorial invariants computing the Ray-Singer analytic torsion. Differential Geom. Appl. 6(1996), 351–366.Google Scholar
[Fr] Fried, D., Torsion and closed geodesics on complex hyperbolic manifolds. Invent.Math. 91Z(1988), 31–51.Google Scholar
[FK] Fuglede, B. and Kadison, R. V., Determinant theory in finite factors. Ann. of Math. 55(1952), 520–530.Google Scholar
[Gau] Gauduchon, P., Le thèoréme de l’excentricité nulle. C. R. Acad. Sci. Paris Sér. A 285(1977), 387–390.Google Scholar
[Ge] Getzler, E., A short proof of the local Atiyah-Singer index theorem. Topology 25(1986), 111–117.Google Scholar
[Gi] Gilkey, P. B., Invariance theory, the heat equation and the Atiyah-Singer index theorem. Mathematics Lecture Series 11, Publish or Perish, Inc., Wilmington, DE, 1984.Google Scholar
[G] Gromov, M., Kähler-hyperbolicity and L2 Hodge theory. J. Differential Geom. 33(1991), 263–292.Google Scholar
[GS] Gromov, M. and Shubin, M., Von Neumann spectra near zero. Geophys. Astrophys. Fluid Dynamics 1(1991), 375–404.Google Scholar
[HS] de la Harpe, P. and Skandalis, G., Déterminant associé à une trace sur une algèbre de Banach. Ann. Inst. Fourier (Grenoble) 34(1984), 241–260.Google Scholar
[HT] Hakeda, J. and Tomiyama, J., On some extension properties of von Neumann algebras. Tôhoku Math. J. (2) 19(1967), 315–323.Google Scholar
[Lang] Lang, S., Differential and Riemannian manifolds. Graduate Texts in Math. 160, Springer Verlag, 1995.Google Scholar
[L] Lott, J., Heat kernels on covering spaces and topological invariants. J. Differential Geom. 35(1992), 471–510.Google Scholar
[Lu] Lück, W., Approximating L2-invariants by their finite-dimensional analogues. Geom. Funct. Anal. 4(1994), 455–481.Google Scholar
[M] Mathai, V., L2-analytic torsion. J. Funct. Anal. 107(1992), 369–386.Google Scholar
[Ph] Phillips, J., Perturbations of type I von Neumann algebras. Pacific J. Math. (1974), 505–511.Google Scholar
[Q] Quillen, D. G., Determinants of Cauchy-Riemann operators over a compact Riemann surface. Functional Anal. Appl. 19(1985), 31–34.Google Scholar
[Ran] Randol, B., On the analytic continuation of theMinakshisundaram-Pleijel zeta function for compact Riemann surfaces. Trans. Amer.Math. Soc. 201(1975), 241–246.Google Scholar
[RS] Ray, D. B. and Singer, I. M., Analytic Torsion for Complex Manifolds. Ann. of Math. 98(1973), 154–177.Google Scholar
[RS1] Ray, D. B. and Singer, I. M., R-torsion and the Laplacian on Riemannian manifolds. Adv. in Math. 7(1971), 145–210.Google Scholar
[R] Roe, J., Elliptic operators, topology and asymptotic methods. Longman Scientific and Technical, 1988.Google Scholar
[Sc] Schick, T., preprint, 1998.Google Scholar