Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:09:30.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic Evaluations of Some Euler Integrals, Duplication Formulae for Appell's Hypergeometric Function F1, and Brownian Variations

Published online by Cambridge University Press:  20 November 2018

Mourad E. H. Ismail  and
Jim Pitman
Mourad E. H. Ismail
Affiliation:
Department of Mathematics, University of South Florida, Tampa, FL 33620-5700, USA email: [email protected]
Jim Pitman
Affiliation:
Department of Statistics, University of California-Berkeley, Berkeley, CA 94720-3860, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

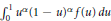Explicit evaluations of the symmetric Euler integral $\int _{0}^{1}\,{{u}^{\alpha }}{{(1-u)}^{\alpha }}f(u)\,du$ are obtained for some particular functions 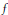$f$. These evaluations are related to duplication formulae for Appell’s hypergeometric function 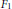${{F}_{1}}$ which give reductions of 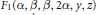${{F}_{1}}(\alpha ,\beta ,\beta ,2\alpha ,y,z)$ in terms of more elementary functions for arbitrary 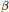$\beta $ with 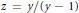$z=y/(y-1)$ and for 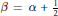$\beta =\alpha +\frac{1}{2}$ with arbitrary 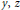$y,z$. These duplication formulae generalize the evaluations of some symmetric Euler integrals implied by the following result: if a standard Brownian bridge is sampled at time 0, time 1, and at $n$ independent randomtimes with uniformdistribution on 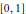$[0,1]$, then the broken line approximation to the bridge obtained from these 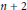$n+2$ values has a total variation whose mean square is 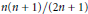$n(n+1)/(2n+1)$.

Keywords

33C6560J65Brownian bridgeGauss’s hypergeometric functionLauricella’s multiple hypergeometric seriesuniform order statisticsAppell functions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 5 , 01 October 2000 , pp. 961 - 981
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions. Dover, New York, 1965.Google Scholar
[2] Aldous, D. J., Exchangeability and related topics. In: École d’Été de Probabilités de Saint-Flour XII (ed. Hennequin, P. L.), Lecture Notes in Math. 1117. Springer-Verlag, 1985.Google Scholar
[3] Andrews, G. E., Askey, R., and Roy, R., Special Functions. Encyclopedia ofMath. andAppl. Vol. 71. Cambridge Univ. Press, Cambridge, 1999.Google Scholar
[4] Appell, P., Sur les fonctions hypergéométriques de plusieurs variables. Gauthier-Villars, Paris, 1925. Mém. des Sciences Math. de l’Acad. des Sciences de Paris, III.Google Scholar
[5] Appell, P. and Kampé de Fériet, J., Fonctions Hypergéométriques et Hypersphériques: Polynômes d’Hermite. Gauthier-Villars, Paris, 1926.Google Scholar
[6] Bailey, W. N., Generalized Hypergeometric Series. Cambridge Univ. Press, Cambridge, 1935.Google Scholar
[7] Burchnall, J. L. and Chaundry, T. W., Expansions of Appell's double hypergeometric functions II. Quart. J. Math Oxford Ser. 12(1941), 112–128.Google Scholar
[8] Erdélyi, A. et al., Higher Transcendental Functions. Bateman Manuscript Project, Vol. 1. McGraw-Hill, New York, 1953.Google Scholar
[9] Erdélyi, A. et al, Higher Transcendental Functions. Bateman Manuscript Project, Vol. 2. McGraw-Hill, New York, 1953.Google Scholar
[10] Exton, H., Multiple hypergeometric functions and applications. Ellis Horwood Ltd., Chichester, 1976.Google Scholar
[11] Exton, H., Handbook of hypergeometric integrals. Ellis Horwood Ltd., Chichester, 1978.Google Scholar
[12] Feller, W., An Introduction to Probability Theory and its Applications. Vol. 1, rd edition, Wiley, 3New York, 1968.Google Scholar
[13] Felle, W., An Introduction to Probability Theory and its Applications. Vol. 2, 2nd edition, Wiley, New York, 1971.Google Scholar
[14] Fields, J. L. and Ismail, M. E. H., Polynomial expansions. Math. Comp. 29(1975), 894–902.Google Scholar
[15] Fields, J. L. and Wimp, J., Expansions of hypergeometric functions in hypergeometric functions. Math. Comp. 15(1961), 390–395.Google Scholar
[16] Gessel, I. M., Super ballot numbers. J. Symbolic Comput. (2–3) 14(1992), 179–194.Google Scholar
[17] Karlsson, P. W., Reduction of certain generalised Kampé de Fériet functions. Math. Scand. 32(1973), 265–268.Google Scholar
[18] Lauricella, G., Sulle funzioni hypergeometriche a piu variabli. Rendiconti del Circolo Matematico di Palermo 7(1893), 111–158.Google Scholar
[19] Lebedev, N. N., Special Functions and their Applications. Prentice-Hall, Englewood Cliffs, NJ, 1965.Google Scholar
[20] Lévy, P., Sur certains processus stochastiques homogènes. Compositio Math. 7(1939), 283–339.Google Scholar
[21] Lyubich, M. Yu., The dynamics of rational transforms: the topological picture. Russian Math. Surveys 41(1986), 43–117.Google Scholar
[22] Nevai, P., Géza Freud, orthogonal polynomials and Christoffel functions. A case study. J. Approx. Theory 48(1986), 3–167.Google Scholar
[23] Picard, E., Sur une extension aux fonctions de deux variables du problème de Riemann relatif aux fonctions hypergéometriques. C. R. Acad. Sci. Paris 90(1880), 1119 and 1267.Google Scholar
[24] Pitman, J., Brownian motion, bridge, excursion and meander characterized by sampling at independent uniform times. Electron. J. Probab. (11) 4(1999), 1–33.Google Scholar
[25] Pitman, J. and Yor, M., Arcsine laws and interval partitions derived from a stable subordinator. Proc. London Math. Soc. Ser. (3) 65(1992), 326–356.Google Scholar
[26] Revuz, D. and Yor, M., Continuous martingales and Brownian motion. 2nd edition, Springer, Berlin-Heidelberg, 1994.Google Scholar
[27] Shorack, G. R. and Wellner, J. A., Empirical processes with applications to statistics. John Wiley & Sons, New York, 1986.Google Scholar
[28] Slater, L. J., Generalized Hypergeometric Functions. Cambridge Univ. Press, Cambridge, 1966.Google Scholar
[29] Springer, M. D., Review of “Selected tables in mathematical statistics (Vol. VII). The product of two normally distributed random variables” by W. Q. Meeker Jr., L. W. Cornwell and L. A. Aroian. Technometrics 25(1983), 211–212.Google Scholar
[30] Ueno, K., Hypergeometric series formulas generated by the Chu-Vandermonde convolution. Mem. Fac. Sci. Kyushu Univ. Ser. A (1) 44(1990), 11–26.Google Scholar
[31] Ueno, K., Hypergeometric series formulas through operator calculus. Funkcial. Ekvac. (3) 33(1990), 493–518.Google Scholar
[32] Ulam, S. M. and vonNeumann, J., On combination of stochastic and deterministic processes. Bull.Amer.Math. Soc. 53(1947), 1120.Google Scholar