Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T20:04:44.745Z Has data issue: false hasContentIssue false
  • English
  • Français

On Orbit Closures of Symmetric Subgroups in Flag Varieties

Published online by Cambridge University Press:  20 November 2018

Michel Brion  and
Aloysius G. Helminck
Michel Brion
Affiliation:
Université de Grenoble I, Département de Mathématiques, Institut Fourier, UMR 5582 du CNRS, 38402 Saint-Martin d’Hères Cedex, France email: [email protected]
Aloysius G. Helminck
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

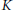We study $K$-orbits in 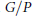$G/P$ where 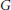$G$ is a complex connected reductive group, $P\,\subseteq \,G$ is a parabolic subgroup, and 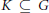$K\,\subseteq \,G$ is the fixed point subgroup of an involutive automorphism 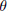$\theta$. Generalizing work of Springer, we parametrize the (finite) orbit set 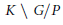$K\,\backslash \,G/P$ and we determine the isotropy groups. As a consequence, we describe the closed (resp. affine) orbits in terms of 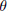$\theta$-stable (resp. 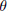$\theta$-split) parabolic subgroups. We also describe the decomposition of any 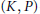$(K,\,P)$-double coset in 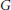$G$ into 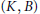$(K,\,B)$-double cosets, where 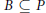$B\,\subseteq \,P$ is a Borel subgroup. Finally, for certain 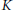$K$-orbit closures 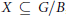$X\,\subseteq \,G/B$, and for any homogeneous line bundle 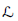$\mathcal{L}$ on 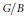$G/B$ having nonzero global sections, we show that the restriction map 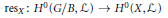$\text{re}{{\text{s}}_{X}}\,:\,{{H}^{0}}\,\left( G\,/\,B,\,\mathcal{L} \right)\,\to \,{{H}^{0}}\,\left( X,\,\mathcal{L} \right)$ is surjective and that 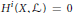${{H}^{i}}\,\left( X,\mathcal{L} \right)\,=\,0$ for 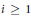$i\,\ge \,1$. Moreover, we describe the 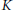$K$-module 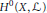${{H}^{0}}\left( X,L \right)$. This gives information on the restriction to 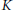$K$ of the simple 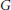$G$-module 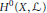${{H}^{0}}\,\left( G\,/\,B,\mathcal{L} \right)$. Our construction is a geometric analogue of Vogan and Sepanski’s approach to extremal 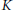$K$-types.

Keywords

14M1520G05flag varietysymmetric subgroup
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 2 , 01 April 2000 , pp. 265 - 292
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Barbasch, D. and Evens, S., K-orbits on Grassmannians and a PRV conjecture for real groups. J. Algebra 167(1994), 258–283.Google Scholar
[2] Borel, A., Linear algebraic groups. 2nd enlarged edition, Graduate Texts in Math. 126, Springer-Verlag, New York, 1991.Google Scholar
[3] Borel, A. and Tits, J., Groupes réductifs. Inst. Hautes Études Sci. Publ. Math. 27(1965), 55–150.Google Scholar
[4] Brion, M., On the general faces of the moment polytope. Internat.Math. Res. Notices 4(1999), 185–201.Google Scholar
[5] Brundan, J., Multiplicity-free subgroups of reductive algebraic groups. J. Algebra 188(1997), 310–330.Google Scholar
[6] Brundan, J., Dense orbits and double cosets. In: Algebraic groups and their representations (Cambridge, 1997), NATOAdv. Sci. Inst. Ser. C Math. Phys. Sci. 517, Kluwer Acad. Publ., Dordrecht, 1998, 259–274.Google Scholar
[7] Helminck, A. G., Tori invariant under an involutorial automorphism I. Adv. in Math. (1) 85(1991), 1–38.Google Scholar
[8] Helminck, A. G., Tori invariant under an involutorial automorphism II. Adv. in Math. (1) 131(1997), 1–92.Google Scholar
[9] Helminck, A. G. and Wang, S. P., On rationality properties of involutions of reductive groups. Adv. in Math. 99(1993), 26–97.Google Scholar
[10] Krämer, M., Multiplicity-free subgroups of compact connected Lie groups. Arch. Math. 27(1976), 28–36.Google Scholar
[11] Ramanathan, A., Equations defining Schubert varieties and Frobenius splitting of diagonals. Inst. Hautes Études Sci. Publ. Math. 65(1987), 61–90.Google Scholar
[12] Ramanan, S. and Ramanathan, A., Projective normality of flag varieties and Schubert varieties. Invent. Math. 79(1985), 217–224.Google Scholar
[13] Richardson, R. W. and Springer, T. A., The Bruhat order on symmetric varieties. Geom. Dedicata 35(1990), 389–436.Google Scholar
[14] Richardson, R. W. and Springer, T. A., Combinatorics and geometry of K-orbits on the flag manifold. In: Linear algebraic groups and their representations, Contemp.Math. 153, Amer. Math. Soc., 1993, 109–142.Google Scholar
[15] Sepanski, M. R., Boundary of K-types, restriction of cohomology, and the multiplicity-free case. Compositio Math. 106(1997), 31–41.Google Scholar
[16] Springer, T. A., Some results on algebraic groups with involutions. In: Algebraic groups and related topics, Adv. Stud. Pure Math. 6, Kinokuniya-North Holland, 1985, 525–543.Google Scholar
[17] Steinberg, R., Endomorphisms of linear algebraic groups. Mem. Amer. Math. Soc. 80, 1968.Google Scholar