Let $Y$ be an infinite covering space of a projective manifold 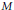$M$ in 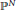${{\mathbb{P}}^{N}}$ of dimension 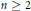$n\ge 2$. Let 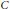$C$ be the intersection with 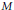$M$ of at most 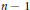$n-1$ generic hypersurfaces of degree 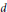$d$ in 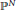${{\mathbb{P}}^{N}}$. The preimage 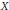$X$ of 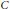$C$ in $Y$ is a connected submanifold. Let 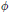$\phi$ be the smoothed distance from a fixed point in $Y$ in a metric pulled up from 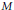$M$. Let 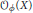${{\mathcal{O}}_{\phi }}(X)$ be the Hilbert space of holomorphic functions 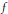$f$ on 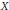$X$ such that 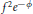${{f}^{2}}{{e}^{-\phi }}$ is integrable on 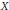$X$, and define 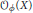${{\mathcal{O}}_{\phi }}(X)$ similarly. Our main result is that (under more general hypotheses than described here) the restriction 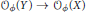${{\mathcal{O}}_{\phi }}(Y)\to {{\mathcal{O}}_{\phi }}(X)$ is an isomorphism for 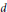$d$ large enough.

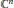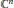This yields new examples of Riemann surfaces and domains of holomorphy in ${{\mathbb{C}}^{n}}$ with corona. We consider the important special case when $Y$ is the unit ball $\mathbb{B}$ in ${{\mathbb{C}}^{n}}$, and show that for 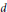$d$ large enough, every bounded holomorphic function on 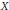$X$ extends to a unique function in the intersection of all the nontrivial weighted Bergman spaces on $\mathbb{B}$. Finally, assuming that the covering group is arithmetic, we establish three dichotomies concerning the extension of bounded holomorphic and harmonic functions from 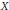$X$ to $\mathbb{B}$.