Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Favini, Angelo
Goldstein, Gisèle Ruiz
Goldstein, Jerome A.
and
Romanelli, Silvia
2008.
Fourth Order Operators With General Wentzell Boundary Conditions.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 2,
Aliyev, Ziyatkhan
2014.
Some global results for nonlinear fourth order eigenvalue problems.
Open Mathematics,
Vol. 12,
Issue. 12,
Aliyev, Ziyatkhan S.
and
Rzayeva, Humay Sh.
2015.
Oscillation properties for the equation of the relativistic quantum theory.
Applied Mathematics and Computation,
Vol. 271,
Issue. ,
p.
308.
Aliyev, Z. S.
and
Asadov, X. A.
2021.
Global Bifurcation from Zero in Some Fourth-Order Nonlinear Eigenvalue Problems.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 44,
Issue. 2,
p.
981.
Aliyev, Ziyatkhan S.
and
Ismayilova, Nurida A.
2023.
Global bifurcation from zero in nonlinear Sturm-Liouville equation with a spectral parameter in the boundary condition.
Quaestiones Mathematicae,
Vol. 46,
Issue. 11,
p.
2233.
Aliyev, Ziyatkhan S.
Hadiyeva, Sevinj S.
and
Ismayilova, Nurida A.
2023.
Global Bifurcation from Infinity in Some Nonlinear Sturm-Liouville Problems.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 3,
Aliyev, Ziyatkhan S.
and
Aliyeva, Yagut N.
2023.
Global bifurcation results for some fourth‐order nonlinear eigenvalue problem with a spectral parameter in the boundary condition.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 1,
p.
1282.
Aliyev, Ziyatkhan
and
Aliyeva, Yagut
2024.
Existence of nodal solutions to some nonlinear boundary value problems for ordinary differential equations of fourth order.
Electronic Journal of Qualitative Theory of Differential Equations,
p.
1.
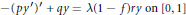 $$-{{\left( p{y}' \right)}^{\prime }}\,+\,qy\,=\,\text{ }\!\!\lambda\!\!\text{ }\left( 1-f \right)ry\,on\,[0,\,1]$$
$$-{{\left( p{y}' \right)}^{\prime }}\,+\,qy\,=\,\text{ }\!\!\lambda\!\!\text{ }\left( 1-f \right)ry\,on\,[0,\,1]$$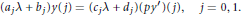 $$\left( {{\text{a}}_{j}}\text{ }\lambda \text{ }\text{+}{{\text{b}}_{j}} \right)y\left( j \right)=\left( {{c}_{j}}\text{ }\lambda \text{ }+{{d}_{j}} \right)\left( p{y}' \right)\left( j \right),j=0,1$$
$$\left( {{\text{a}}_{j}}\text{ }\lambda \text{ }\text{+}{{\text{b}}_{j}} \right)y\left( j \right)=\left( {{c}_{j}}\text{ }\lambda \text{ }+{{d}_{j}} \right)\left( p{y}' \right)\left( j \right),j=0,1$$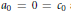 ${{\text{a}}_{0}}\,=\,0\,=\,{{c}_{0}}$ and
${{\text{a}}_{0}}\,=\,0\,=\,{{c}_{0}}$ and 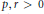 $p,\,r\,>\,0$ and
$p,\,r\,>\,0$ and 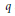 $q$ are functions depending on the independent variable
$q$ are functions depending on the independent variable 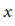 $x$ alone, while
$x$ alone, while 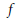 $f$ depends on
$f$ depends on 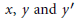 $x,\,y\,and\,{y}'$. Results are given on existence and location of sets of
$x,\,y\,and\,{y}'$. Results are given on existence and location of sets of 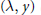 $(\lambda ,\,y)$ bifurcating from the linearized eigenvalues, and for which
$(\lambda ,\,y)$ bifurcating from the linearized eigenvalues, and for which 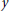 $y$ has prescribed oscillation count, and on completeness of the
$y$ has prescribed oscillation count, and on completeness of the 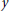 $y$ in an appropriate sense.
$y$ in an appropriate sense.