Examples of normed barrelled spaces E or quasicomplete barrelled spaces E are given such that there is a non-continuous linear map from the space E into itself with closed graph.

For a finite group G and a subset S of G with 1 ∉ S, the Cayley graph Cay(G, S) is the digraph with vertex set G such that (x, y) is an arc if and only if yx−1 ∈ S. The Cayley graph Cay(G, S) is called a CI-graph if, for any T ⊂ G, whenever Cay (G, S) ≅ Cay(G, T) there is an element a σ ∈ Aut(G) such that Sσ = T. For a positive integer m, G is called an m-DCI-group if all Cayley graphs of G of valency at most m are CI-graphs; G is called a connected m-DCI-group if all connected Cayley graphs of G of valency at most m are CI-graphs. The problem of determining Abelian m-DCI-groups is a long-standing open problem. It is known from previous work that all Abelian m-DCI-groups lie in an explicitly determined class of Abelian groups. First we reduce the problem of determining Abelian m-DCI-groups to the problem of determining whether every subgroup of a member of is a connected m-DCI-group. Then (for a finite group G, letting p be the least prime divisor of |G|,) we completely classify Abelian connected (p + 1)-DCI-groups G, and as a corollary, we completely classify Abelian m-DCI-groups G for m ≤ p + 1. This gives many earlier results when p = 2.

In this paper the equation x2 + 32k = yn where n ≥ 3 is studied. For n = 3, it is proved that it has a solution only if k = 3K + 2 and then there is a unique solution x = 46 × 33K and y = 13 × 32K. For n > 3 theorems are proved which determine a large number of values of k and n for which this equation has no solution. It is proved that if this equation has a solution for n > 3, then n is odd and k = 2δ.k′ where δ ≥ 1, (2, δ) = 1, k′ ≡ 15 (mod 20) and all the primes divisors p of n are congruent to 11 (mod 12).

We improve upon earlier effective bounds for the magnitude of integer points on an elliptic curve ε defined over a number field K. We slightly refine the dependence on the discriminant of K. In most of the previous papers, the estimates obtained are exponential in the height of ε. In this work, taking also into consideration the prime ideals dividing the discriminant of ε, we provide a totally explicit bound which is only polynomial in the height.

For a continuous function f(t) on (0, ∞) which is strictly monotone and a probability measure μ on [0, 1] we introduce the functional mean and the harmonic functional mean of x > 0 and y > 0 with respect to μ by

which gives a unified approach to various famous means.

Moreover, functional means and harmonic means in n variables are also given and applied to get many interesting properties, such as

where

In this paper, we introduce the notion of exterior space and give a full embedding of the category P of spaces and proper maps into the category E of exterior spaces. We show that the category E admits the structure of a closed simplicial model category. This technique solves the problem of using homotopy constructions available in the localised category HoE and in the “homotopy category” π0E, which can not be developed in the proper homotopy category.

On the other hand, for compact metrisable spaces we have formulated sets of shape morphisms, discrete shape morphisms and strong shape morphisms in terms of sets of exterior homotopy classes and for the case of finite covering dimension in terms of homomorphism sets in the localised category.

As applications, we give a new version of the Whitehead Theorem for proper homotopy and an exact sequence that generalises Quigley's exact sequence and contains the shape version of Edwards-Hastings' Comparison Theorem.

We examine the permutation properties of the polynomials of the type hk, r, s(x) = xr (1 + xs + … + xsk) over the finite field , of characteristic p. We give sufficient and necessary conditions in terms of k and r for hk, r, l(x) to be a permutation polynomial over , for q = p or p2. We also prove that if hk, r, s(x) is a permutation polynomial over , then (k + 1)s = ±1.

Sharp gradient estimates are derived for positive eigenfunctions on complete Riemannian manifolds with Ricci curvature bounded below.

Let 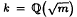be a real quadratic field. It is well known that if 3 divides the class number of k, then 3 divides the class number of 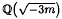, and thus it divides B1,χω−1, where χ and ω are characters belonging to the fields k and 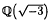respectively. In general, the main conjecture of Iwasawa theory implies that if an odd prime p divides the class number of k, then p divides B1,χω−1, where ω is the Teichmüller character for p.

The aim of this paper is to examine its converse when p splits in k. Let k∞ be the ℤp-extension of k = k0 and hn be the class number of kn, the n th layer of the ℤp-extension. We shall prove that if p |B1,χω−1, then p | hn for all n ≥ 1. In terms of Iwasawa theory, this amounts to saying that if M∞/k∞, is nontrivial, then L∞/k∞ is nontrivial, where M∞ and L∞ are the maximal abelian p-extensions unramified outside p and unramified everywhere respectively.

A quadrature formula for a variable-signed weight function w(x) is constructed using Hermite interpolating polynomials. We show its mean and quadratic mean convergence. We also discuss the rate of convergence in terms of the modulus of continuity for higher order derivatives with respect to the sup norm.

The isodiametric problem in the Euclidean plane is solved for bounded convex sets, which are symmetric about the origin, and which contain no interior non-zero point of an arbitrary lattice L.

In this paper, we study submanifolds in the unit hypersphere satisfying where is the quadric representation of the submanifold, and B and C are two constant matrices. We prove that the totally geodesic submanifolds are the only submanifolds in the unit hypersphere whose quadric representations satisfy

The problem of exponential stability of the problem of transmission of the wave equation with lower-order terms is considered. Making use of the classical energy method and multiplier technique, we prove that this problem of transmission is exponentially stable.

The connection between Clifford analysis and the Weyl functional calculus for an n-tuple of bounded selfadjoint operators is noted. The operators do not necessarily commute with each other.

In this paper, we prove that there exist two finite sets S1 (with 1 element) and S2 (with 3 elements) such that any two entire functions f and g satisfying Ef(Sj) = Eg(Sj) for j = 1, 2 must be identical. This answers a question posed by Gross. Examples are provided to show that this result is sharp.