Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T02:17:18.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphisms of Cayley digraphs of Abelian groups

Published online by Cambridge University Press:  17 April 2009

Cai Heng Li
Cai Heng Li
Affiliation:
Department of MathematicsUniversity of Western AustraliaNedlands WA 6907Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite group G and a subset S of G with 1 ∉ S, the Cayley graph Cay(G, S) is the digraph with vertex set G such that (x, y) is an arc if and only if yx−1 ∈ S. The Cayley graph Cay(G, S) is called a CI-graph if, for any T ⊂ G, whenever Cay (G, S) ≅ Cay(G, T) there is an element a σ ∈ Aut(G) such that Sσ = T. For a positive integer m, G is called an m-DCI-group if all Cayley graphs of G of valency at most m are CI-graphs; G is called a connected m-DCI-group if all connected Cayley graphs of G of valency at most m are CI-graphs. The problem of determining Abelian m-DCI-groups is a long-standing open problem. It is known from previous work that all Abelian m-DCI-groups lie in an explicitly determined class 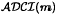of Abelian groups. First we reduce the problem of determining Abelian m-DCI-groups to the problem of determining whether every subgroup of a member of 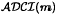is a connected m-DCI-group. Then (for a finite group G, letting p be the least prime divisor of |G|,) we completely classify Abelian connected (p + 1)-DCI-groups G, and as a corollary, we completely classify Abelian m-DCI-groups G for m ≤ p + 1. This gives many earlier results when p = 2.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 57 , Issue 2 , April 1998 , pp. 181 - 188
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Adám, A., ‘Research problem 2–10’, J. Combin. Theory 2 (1967), 309.Google Scholar
[2]Alspach, B. and Parsons, T.D., ‘Isomorphisms of circulant graphs and digraphs’, Discrete Math. 25 (1979), 97–108.CrossRefGoogle Scholar
[3]Babai, L. ‘Isomorphism problem for a class of point-symmetric structures’ Acta Math. Acta. Sci. Hungary 29 (1977), 329–336.CrossRefGoogle Scholar
[4]Babai, L. and Frankl, P., ‘Isomorphisms of Cayley graphs I’, Colloq. Math. Soc. János Bolyai 18 (1978), 35–52.Google Scholar
[5]Delorme, C., Favaron, O. and Maheo, M., ‘Isomorphisms of Cayley multigraphs of degree 4 on finite Abelian groups’, European J. Combin. 13 (1992), 59–61.CrossRefGoogle Scholar
[6]Dobson, E., ‘Isomorphism problem for Cayley graphs of ’, Discrete Math. 147 (1995), 87–94.CrossRefGoogle Scholar
[7]Elspas, B. and Turner, J., ‘Graphs with circulant adjacency matrices’, J. Combin. Theory 9 (1970), 297–307.CrossRefGoogle Scholar
[8]Fang, X.G., ‘A characterization of finite Abelian 2-DCI groups’, (in Chinese), J. Math. (Wuhan) 8 (1988), 315–317.Google Scholar
[9]Fang, X.G., ‘Abelian 3-DCI groups’, Ars Combin. 32 (1992), 263–267.Google Scholar
[10]Fang, X.G. and Xu, M.Y., ‘Abelian 3-DCI groups of odd order’, Ars Combin. 28 (1988), 247–251.Google Scholar
[11]Godsil, C.D., ‘On Cayley graph isomorphisms’, Ars Combin. 15 (1983), 231–246.Google Scholar
[12]Li, C.H., ‘Abelian 4-DCI groups’, J. Yunnan Normal University 11 (1991), 24–27.Google Scholar
[13]Li, C.H., ‘On Cayley graphs of Abelian groups’, J. Algebraic Combin. (to appear).Google Scholar
[14]Li, C.H., ‘On isomorphisms of connected Cayley graphs’, Discrete Math. (to appear).Google Scholar
[15]Li, C.H., ‘Isomorphisms of connected Cayley digraphs’, Graphs Combin. (to appear).Google Scholar
[16]Li, C.H., ‘The cyclic groups with the m-DCI property’, European J. Combin. 18 (1997), 655–665.Google Scholar
[17]Li, C.H., Praeger, C.E. and Xu, M.Y., ‘Isomorphisms of finite Cayley digraphs of bounded valency’, J. Combin. Theory Ser. B (to appear).Google Scholar
[18]Muzychuk, M., ‘Ádám's conjecture is true in the square-free case’, J. Combin. Theory Ser. A 72 (1995), 118–134.CrossRefGoogle Scholar
[19]Muzychuk, M., ‘On Ádám's conjecture for circulant graphs’, Discrete Math. 167/168 (1997), 497–510.CrossRefGoogle Scholar
[20]Nowitz, L.A., ‘A nonCayley-invariant Cayley graph of the elementary Abelian group of order 64’, Discrete Math. 110 (1992), 223–228.CrossRefGoogle Scholar
[21]Sun, L., ‘Isomorphisms of circulant graphs’, Chinese Ann. Math. Ser. A 9 (1988), 567–574.Google Scholar
[22]Xu, M.Y. and Meng, J., ‘Weakly 3-DCI Abelian groups’, Austral. J. Combin. 13 (1996), 49–60.Google Scholar