Article contents
Class numbers of real quadratic fields
Published online by Cambridge University Press: 17 April 2009
Abstract
Let 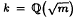 be a real quadratic field. It is well known that if 3 divides the class number of k, then 3 divides the class number of
be a real quadratic field. It is well known that if 3 divides the class number of k, then 3 divides the class number of 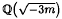 , and thus it divides B1,χω−1, where χ and ω are characters belonging to the fields k and
, and thus it divides B1,χω−1, where χ and ω are characters belonging to the fields k and 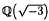 respectively. In general, the main conjecture of Iwasawa theory implies that if an odd prime p divides the class number of k, then p divides B1,χω−1, where ω is the Teichmüller character for p.
respectively. In general, the main conjecture of Iwasawa theory implies that if an odd prime p divides the class number of k, then p divides B1,χω−1, where ω is the Teichmüller character for p.
The aim of this paper is to examine its converse when p splits in k. Let k∞ be the ℤp-extension of k = k0 and hn be the class number of kn, the n th layer of the ℤp-extension. We shall prove that if p |B1,χω−1, then p | hn for all n ≥ 1. In terms of Iwasawa theory, this amounts to saying that if M∞/k∞, is nontrivial, then L∞/k∞ is nontrivial, where M∞ and L∞ are the maximal abelian p-extensions unramified outside p and unramified everywhere respectively.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1998
References
- 2
- Cited by


