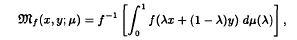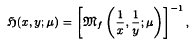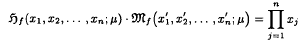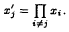Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Neuman, E.
Pearce, C. E. M.
Pečarić, J.
and
Šimić, V.
2003.
The generalised Hadamard inequality, g-convexity and functional Stolarsky means.
Bulletin of the Australian Mathematical Society,
Vol. 68,
Issue. 2,
p.
303.
Yang, Zhen-Hang
Song, Ying-Qing
and
Chu, Yu-Ming
2014.
Sharp bounds for the arithmetic-geometric mean.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Horváth, L.
and
Pečarić, J.
2015.
New versions of weighted multidimensional functional and Stolarsky means.
Acta Mathematica Hungarica,
Vol. 147,
Issue. 1,
p.
81.


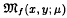 and the harmonic functional mean
and the harmonic functional mean 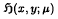 of
of