Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Park, Young Ho
and
Lee, June Bok
2001.
Permutation polynomials and group permutation polynomials.
Bulletin of the Australian Mathematical Society,
Vol. 63,
Issue. 1,
p.
67.
AKBARY, AMIR
ALARIC, SEAN
and
WANG, QIANG
2008.
ON SOME CLASSES OF PERMUTATION POLYNOMIALS.
International Journal of Number Theory,
Vol. 04,
Issue. 01,
p.
121.
ZIEVE, MICHAEL E.
2008.
SOME FAMILIES OF PERMUTATION POLYNOMIALS OVER FINITE FIELDS.
International Journal of Number Theory,
Vol. 04,
Issue. 05,
p.
851.
Zieve, Michael E.
2010.
Additive Number Theory.
p.
355.
Marcos, José E.
2011.
Specific permutation polynomials over finite fields.
Finite Fields and Their Applications,
Vol. 17,
Issue. 2,
p.
105.


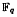 , of characteristic
, of characteristic 