Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-21T01:31:50.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical submanifolds with special quadric representations

Published online by Cambridge University Press:  17 April 2009

Jitan Lu
Jitan Lu
Affiliation:
Division of MathematicsNational Institute of EducationNanyang Technological UniversitySingapore 259756 e-mail: NF2363833U@AC AD21.NTU.EDU.SG
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study submanifolds in the unit hypersphere satisfying 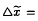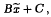where 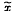is the quadric representation of the submanifold, and B and C are two constant matrices. We prove that the totally geodesic submanifolds are the only submanifolds in the unit hypersphere whose quadric representations satisfy

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 57 , Issue 2 , April 1998 , pp. 295 - 303
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Barros, M. and Chen, B.Y., ‘Spherical submanifolds which are of 2-type via the second standard immersion of the sphere’, Nagoya Math. J. 108 (1987), 77–91.CrossRefGoogle Scholar
[2]Chen, B.Y., Total mean curvature and submanifolds of finite type (World Scientific, 1984).CrossRefGoogle Scholar
[3]Dimitric, I., ‘Quadric representation of a submanifold’, Proc. Amer. Math. Soc. 114 (1992), 201–210.CrossRefGoogle Scholar
[4]Lu, J., ‘Quadric representation of a submanifold with parallel mean curvature vector’, Adv. in Math. (China) 25 (1996), 433–437.Google Scholar
[5]Lu, J., ‘Hypersurface with special quadric representation’, Bull. Austral. Math. Soc. 56 (1997), 227–234.Google Scholar
[6]Lu, J., ‘Submanifolds whose Quadric representations satisfy Kodai Math. J. 20 (1997), 135–142.CrossRefGoogle Scholar